Stein Discrepancy for Unsupervised Domain Adaptation

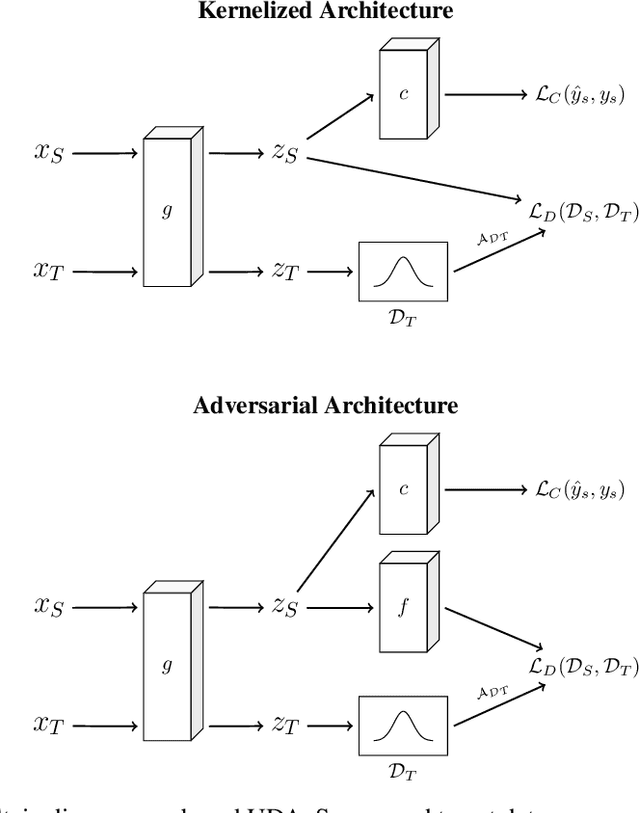
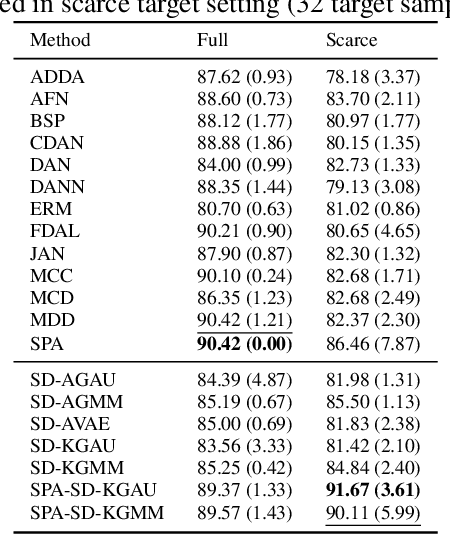
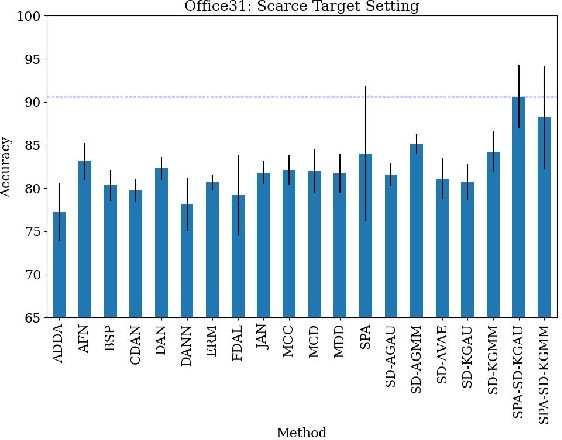
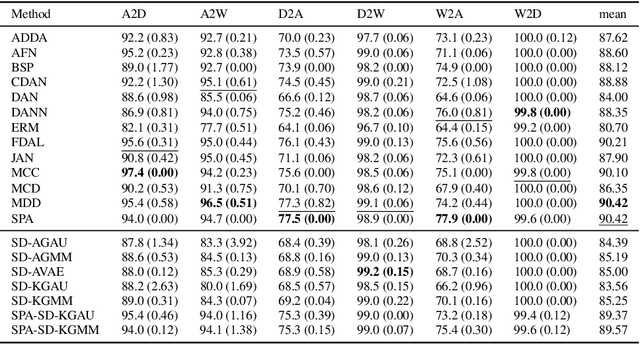
Unsupervised domain adaptation (UDA) leverages information from a labeled source dataset to improve accuracy on a related but unlabeled target dataset. A common approach to UDA is aligning representations from the source and target domains by minimizing the distance between their data distributions. Previous methods have employed distances such as Wasserstein distance and maximum mean discrepancy. However, these approaches are less effective when the target data is significantly scarcer than the source data. Stein discrepancy is an asymmetric distance between distributions that relies on one distribution only through its score function. In this paper, we propose a novel \ac{uda} method that uses Stein discrepancy to measure the distance between source and target domains. We develop a learning framework using both non-kernelized and kernelized Stein discrepancy. Theoretically, we derive an upper bound for the generalization error. Numerical experiments show that our method outperforms existing methods using other domain discrepancy measures when only small amounts of target data are available.

Klein Model for Hyperbolic Neural Networks

Hyperbolic neural networks (HNNs) have been proved effective in modeling complex data structures. However, previous works mainly focused on the Poincar\'e ball model and the hyperboloid model as coordinate representations of the hyperbolic space, often neglecting the Klein model. Despite this, the Klein model offers its distinct advantages thanks to its straight-line geodesics, which facilitates the well-known Einstein midpoint construction, previously leveraged to accompany HNNs in other models. In this work, we introduce a framework for hyperbolic neural networks based on the Klein model. We provide detailed formulation for representing useful operations using the Klein model. We further study the Klein linear layer and prove that the "tangent space construction" of the scalar multiplication and parallel transport are exactly the Einstein scalar multiplication and the Einstein addition, analogous to the M\"obius operations used in the Poincar\'e ball model. We show numerically that the Klein HNN performs on par with the Poincar\'e ball model, providing a third option for HNN that works as a building block for more complicated architectures.

Improving Hyperbolic Representations via Gromov-Wasserstein Regularization

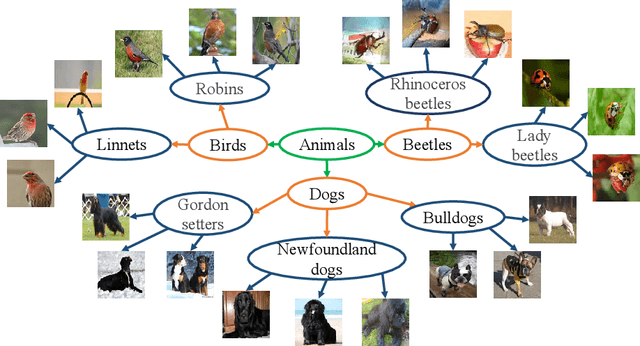
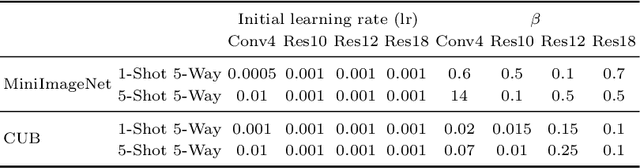
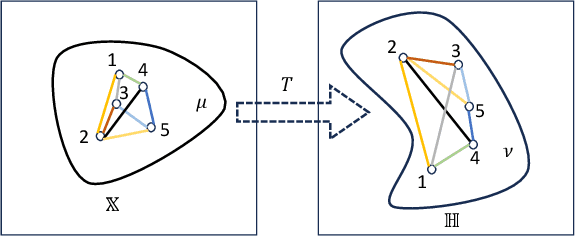
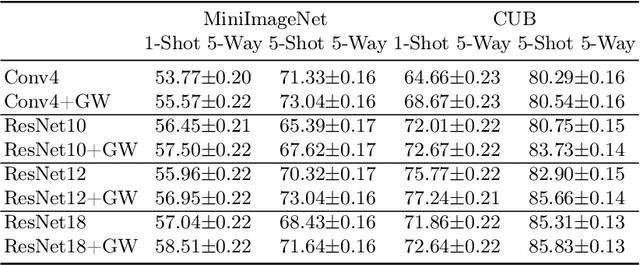
Hyperbolic representations have shown remarkable efficacy in modeling inherent hierarchies and complexities within data structures. Hyperbolic neural networks have been commonly applied for learning such representations from data, but they often fall short in preserving the geometric structures of the original feature spaces. In response to this challenge, our work applies the Gromov-Wasserstein (GW) distance as a novel regularization mechanism within hyperbolic neural networks. The GW distance quantifies how well the original data structure is maintained after embedding the data in a hyperbolic space. Specifically, we explicitly treat the layers of the hyperbolic neural networks as a transport map and calculate the GW distance accordingly. We validate that the GW distance computed based on a training set well approximates the GW distance of the underlying data distribution. Our approach demonstrates consistent enhancements over current state-of-the-art methods across various tasks, including few-shot image classification, as well as semi-supervised graph link prediction and node classification.

Three Revisits to Node-Level Graph Anomaly Detection: Outliers, Message Passing and Hyperbolic Neural Networks

Graph anomaly detection plays a vital role for identifying abnormal instances in complex networks. Despite advancements of methodology based on deep learning in recent years, existing benchmarking approaches exhibit limitations that hinder a comprehensive comparison. In this paper, we revisit datasets and approaches for unsupervised node-level graph anomaly detection tasks from three aspects. Firstly, we introduce outlier injection methods that create more diverse and graph-based anomalies in graph datasets. Secondly, we compare methods employing message passing against those without, uncovering the unexpected decline in performance associated with message passing. Thirdly, we explore the use of hyperbolic neural networks, specifying crucial architecture and loss design that contribute to enhanced performance. Through rigorous experiments and evaluations, our study sheds light on general strategies for improving node-level graph anomaly detection methods.

Interpretable Graph Anomaly Detection using Gradient Attention Maps

Detecting unusual patterns in graph data is a crucial task in data mining. However, existing methods often face challenges in consistently achieving satisfactory performance and lack interpretability, which hinders our understanding of anomaly detection decisions. In this paper, we propose a novel approach to graph anomaly detection that leverages the power of interpretability to enhance performance. Specifically, our method extracts an attention map derived from gradients of graph neural networks, which serves as a basis for scoring anomalies. In addition, we conduct theoretical analysis using synthetic data to validate our method and gain insights into its decision-making process. To demonstrate the effectiveness of our method, we extensively evaluate our approach against state-of-the-art graph anomaly detection techniques. The results consistently demonstrate the superior performance of our method compared to the baselines.

Monotone Generative Modeling via a Gromov-Monge Embedding

Generative Adversarial Networks (GANs) are powerful tools for creating new content, but they face challenges such as sensitivity to starting conditions and mode collapse. To address these issues, we propose a deep generative model that utilizes the Gromov-Monge embedding (GME). It helps identify the low-dimensional structure of the underlying measure of the data and then maps it, while preserving its geometry, into a measure in a low-dimensional latent space, which is then optimally transported to the reference measure. We guarantee the preservation of the underlying geometry by the GME and $c$-cyclical monotonicity of the generative map, where $c$ is an intrinsic embedding cost employed by the GME. The latter property is a first step in guaranteeing better robustness to initialization of parameters and mode collapse. Numerical experiments demonstrate the effectiveness of our approach in generating high-quality images, avoiding mode collapse, and exhibiting robustness to different starting conditions.

Hyperbolic Convolution via Kernel Point Aggregation

Learning representations according to the underlying geometry is of vital importance for non-Euclidean data. Studies have revealed that the hyperbolic space can effectively embed hierarchical or tree-like data. In particular, the few past years have witnessed a rapid development of hyperbolic neural networks. However, it is challenging to learn good hyperbolic representations since common Euclidean neural operations, such as convolution, do not extend to the hyperbolic space. Most hyperbolic neural networks do not embrace the convolution operation and ignore local patterns. Others either only use non-hyperbolic convolution, or miss essential properties such as equivariance to permutation. We propose HKConv, a novel trainable hyperbolic convolution which first correlates trainable local hyperbolic features with fixed kernel points placed in the hyperbolic space, then aggregates the output features within a local neighborhood. HKConv not only expressively learns local features according to the hyperbolic geometry, but also enjoys equivariance to permutation of hyperbolic points and invariance to parallel transport of a local neighborhood. We show that neural networks with HKConv layers advance state-of-the-art in various tasks.

An Unpooling Layer for Graph Generation

We propose a novel and trainable graph unpooling layer for effective graph generation. Given a graph with features, the unpooling layer enlarges this graph and learns its desired new structure and features. Since this unpooling layer is trainable, it can be applied to graph generation either in the decoder of a variational autoencoder or in the generator of a generative adversarial network (GAN). We prove that the unpooled graph remains connected and any connected graph can be sequentially unpooled from a 3-nodes graph. We apply the unpooling layer within the GAN generator. Since the most studied instance of graph generation is molecular generation, we test our ideas in this context. Using the QM9 and ZINC datasets, we demonstrate the improvement obtained by using the unpooling layer instead of an adjacency-matrix-based approach.

Robust Vector Quantized-Variational Autoencoder

Image generative models can learn the distributions of the training data and consequently generate examples by sampling from these distributions. However, when the training dataset is corrupted with outliers, generative models will likely produce examples that are also similar to the outliers. In fact, a small portion of outliers may induce state-of-the-art generative models, such as Vector Quantized-Variational AutoEncoder (VQ-VAE), to learn a significant mode from the outliers. To mitigate this problem, we propose a robust generative model based on VQ-VAE, which we name Robust VQ-VAE (RVQ-VAE). In order to achieve robustness, RVQ-VAE uses two separate codebooks for the inliers and outliers. To ensure the codebooks embed the correct components, we iteratively update the sets of inliers and outliers during each training epoch. To ensure that the encoded data points are matched to the correct codebooks, we quantize using a weighted Euclidean distance, whose weights are determined by directional variances of the codebooks. Both codebooks, together with the encoder and decoder, are trained jointly according to the reconstruction loss and the quantization loss. We experimentally demonstrate that RVQ-VAE is able to generate examples from inliers even if a large portion of the training data points are corrupted.

Hyperbolic Neural Networks for Molecular Generation

With the recent advance of deep learning, neural networks have been extensively used for the task of molecular generation. Many deep generators extract atomic relations from molecular graphs and ignore hierarchical information at both atom and molecule levels. In order to extract such hierarchical information, we propose a novel hyperbolic generative model. Our model contains three parts: first, a fully hyperbolic junction-tree encoder-decoder that embeds the hierarchical information of the molecules in the latent hyperbolic space; second, a latent generative adversarial network for generating the latent embeddings; third, a molecular generator that inherits the decoders from the first part and the latent generator from the second part. We evaluate our model on the ZINC dataset using the MOSES benchmarking platform and achieve competitive results, especially in metrics about structural similarity.