QuadSync: Quadrifocal Tensor Synchronization via Tucker Decomposition

In structure from motion, quadrifocal tensors capture more information than their pairwise counterparts (essential matrices), yet they have often been thought of as impractical and only of theoretical interest. In this work, we challenge such beliefs by providing a new framework to recover $n$ cameras from the corresponding collection of quadrifocal tensors. We form the block quadrifocal tensor and show that it admits a Tucker decomposition whose factor matrices are the stacked camera matrices, and which thus has a multilinear rank of (4,~4,~4,~4) independent of $n$. We develop the first synchronization algorithm for quadrifocal tensors, using Tucker decomposition, alternating direction method of multipliers, and iteratively reweighted least squares. We further establish relationships between the block quadrifocal, trifocal, and bifocal tensors, and introduce an algorithm that jointly synchronizes these three entities. Numerical experiments demonstrate the effectiveness of our methods on modern datasets, indicating the potential and importance of using higher-order information in synchronization.

Tensor-Based Synchronization and the Low-Rankness of the Block Trifocal Tensor

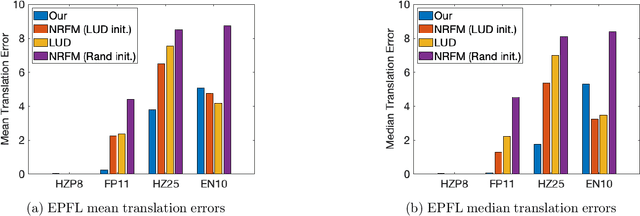
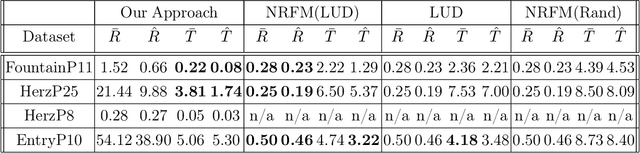
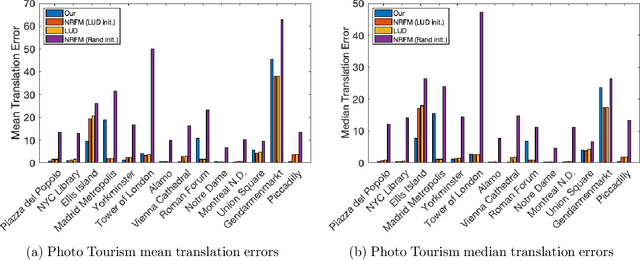
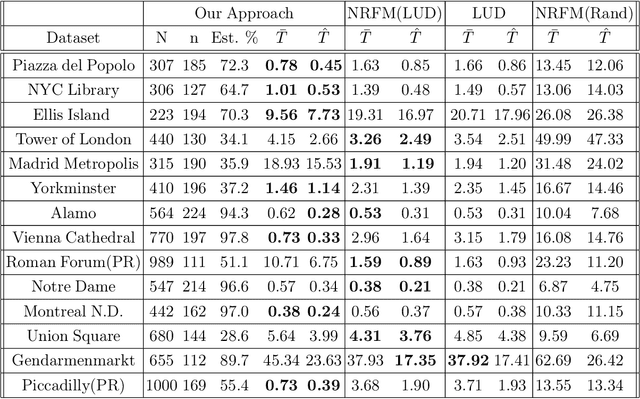
The block tensor of trifocal tensors provides crucial geometric information on the three-view geometry of a scene. The underlying synchronization problem seeks to recover camera poses (locations and orientations up to a global transformation) from the block trifocal tensor. We establish an explicit Tucker factorization of this tensor, revealing a low multilinear rank of $(6,4,4)$ independent of the number of cameras under appropriate scaling conditions. We prove that this rank constraint provides sufficient information for camera recovery in the noiseless case. The constraint motivates a synchronization algorithm based on the higher-order singular value decomposition of the block trifocal tensor. Experimental comparisons with state-of-the-art global synchronization methods on real datasets demonstrate the potential of this algorithm for significantly improving location estimation accuracy. Overall this work suggests that higher-order interactions in synchronization problems can be exploited to improve performance, beyond the usual pairwise-based approaches.