Improved Convergence Rates of Anderson Acceleration for a Large Class of Fixed-Point Iterations

This paper studies Anderson acceleration (AA) for fixed-point methods ${x}^{(k+1)}=q({x}^{(k)})$. It provides the first proof that when the operator $q$ is linear and symmetric, AA improves the root-linear convergence factor over the fixed-point iterations. When $q$ is nonlinear, yet has a symmetric Jacobian at the solution, a slightly modified AA algorithm is proved to have an analogous root-linear convergence factor improvement over fixed-point iterations. Simulations verify our observations. Furthermore, experiments with different data models demonstrate AA is significantly superior to the standard fixed-point methods for Tyler's M-estimation.

Cubic-Regularized Newton for Spectral Constrained Matrix Optimization and its Application to Fairness

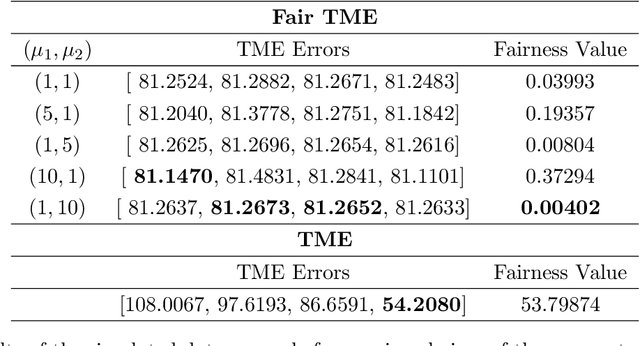
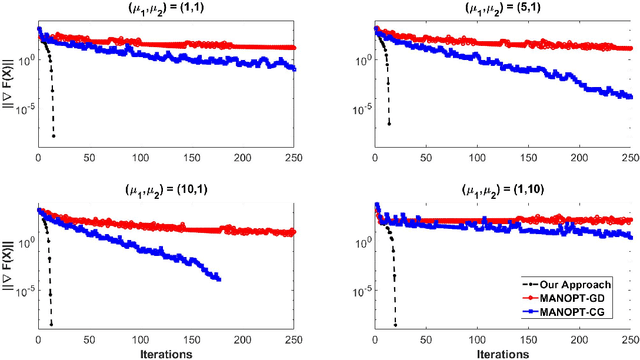
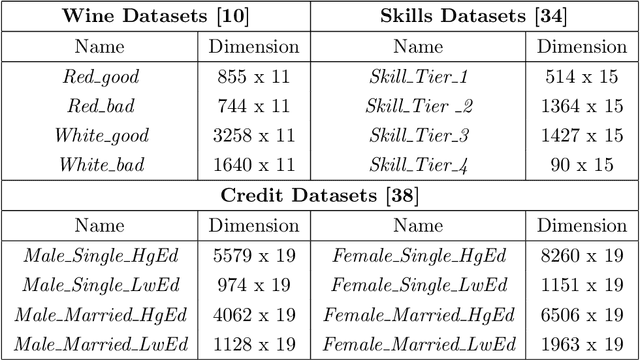
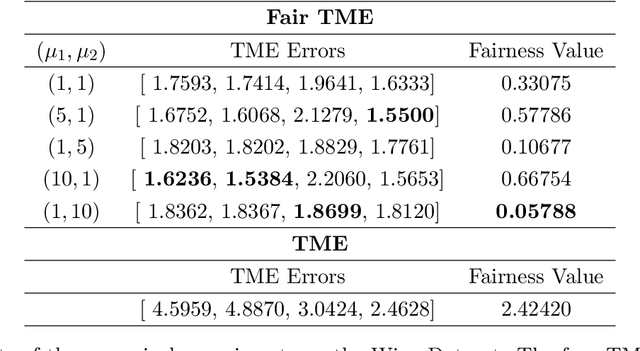
Matrix functions are utilized to rewrite smooth spectral constrained matrix optimization problems as smooth unconstrained problems over the set of symmetric matrices which are then solved via the cubic-regularized Newton method. A second-order chain rule identity for matrix functions is proven to compute the higher-order derivatives to implement cubic-regularized Newton, and a new convergence analysis is provided for cubic-regularized Newton for matrix vector spaces. We demonstrate the applicability of our approach by conducting numerical experiments on both synthetic and real datasets. In our experiments, we formulate a new model for estimating fair and robust covariance matrices in the spirit of the Tyler's M-estimator (TME) model and demonstrate its advantage.

Classifying with Uncertain Data Envelopment Analysis

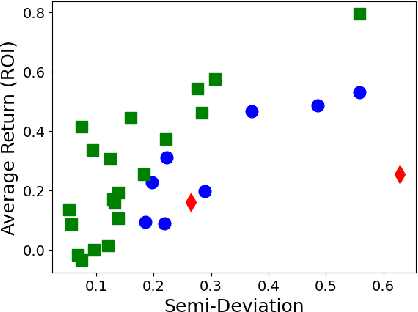
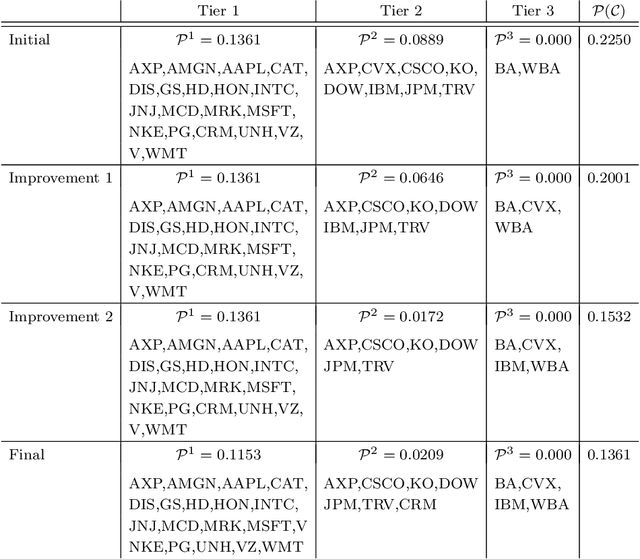
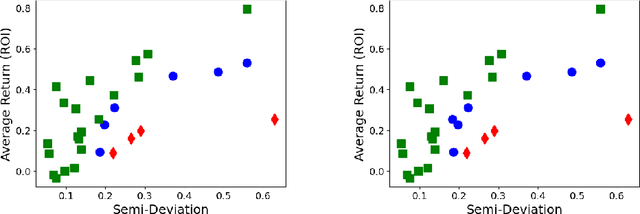
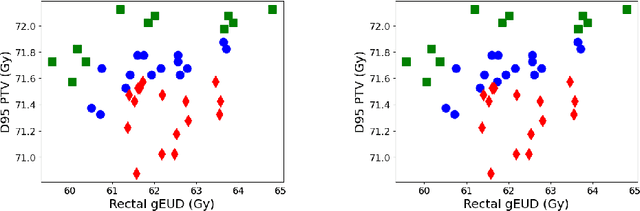
Classifications organize entities into categories that identify similarities within a category and discern dissimilarities among categories, and they powerfully classify information in support of analysis. We propose a new classification scheme premised on the reality of imperfect data. Our computational model uses uncertain data envelopment analysis to define a classification's proximity to equitable efficiency, which is an aggregate measure of intra-similarity within a classification's categories. Our classification process has two overriding computational challenges, those being a loss of convexity and a combinatorially explosive search space. We overcome the first by establishing lower and upper bounds on the proximity value, and then by searching this range with a first-order algorithm. We overcome the second by adapting the p-median problem to initiate our exploration, and by then employing an iterative neighborhood search to finalize a classification. We conclude by classifying the thirty stocks in the Dow Jones Industrial average into performant tiers and by classifying prostate treatments into clinically effectual categories.

HYPPO: A Surrogate-Based Multi-Level Parallelism Tool for Hyperparameter Optimization

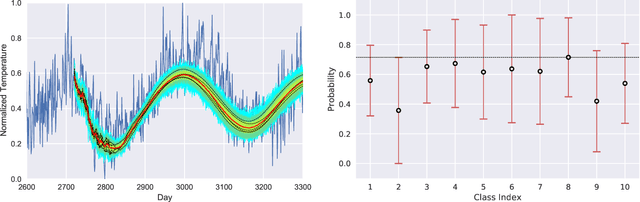
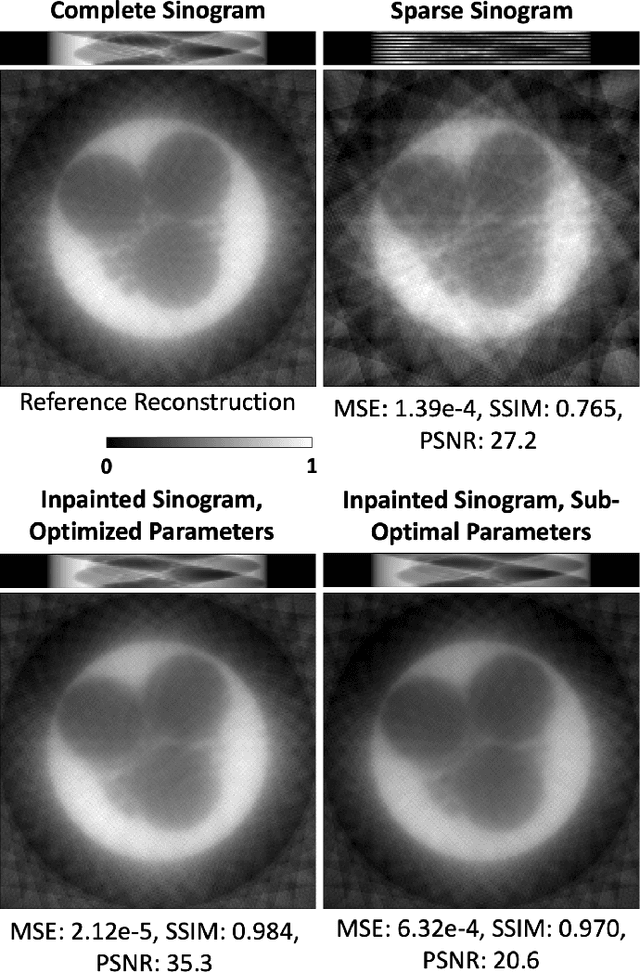
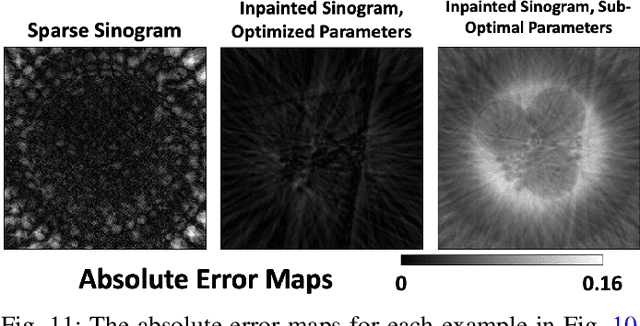
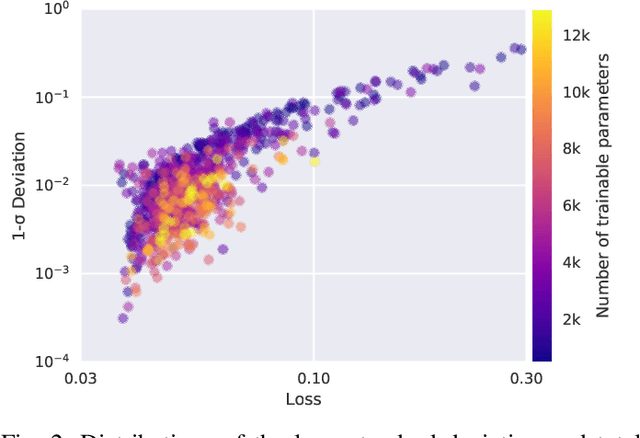
We present a new software, HYPPO, that enables the automatic tuning of hyperparameters of various deep learning (DL) models. Unlike other hyperparameter optimization (HPO) methods, HYPPO uses adaptive surrogate models and directly accounts for uncertainty in model predictions to find accurate and reliable models that make robust predictions. Using asynchronous nested parallelism, we are able to significantly alleviate the computational burden of training complex architectures and quantifying the uncertainty. HYPPO is implemented in Python and can be used with both TensorFlow and PyTorch libraries. We demonstrate various software features on time-series prediction and image classification problems as well as a scientific application in computed tomography image reconstruction. Finally, we show that (1) we can reduce by an order of magnitude the number of evaluations necessary to find the most optimal region in the hyperparameter space and (2) we can reduce by two orders of magnitude the throughput for such HPO process to complete.