Cubic-Regularized Newton for Spectral Constrained Matrix Optimization and its Application to Fairness
Paper and Code
Sep 02, 2022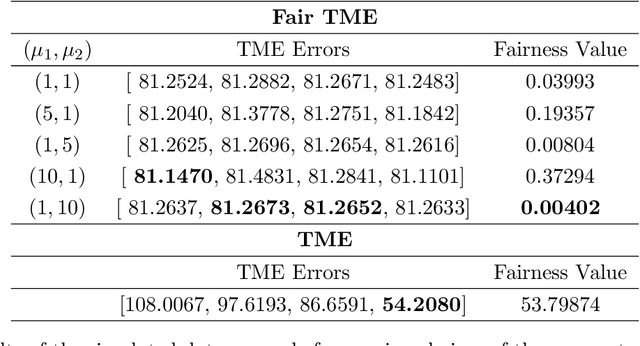
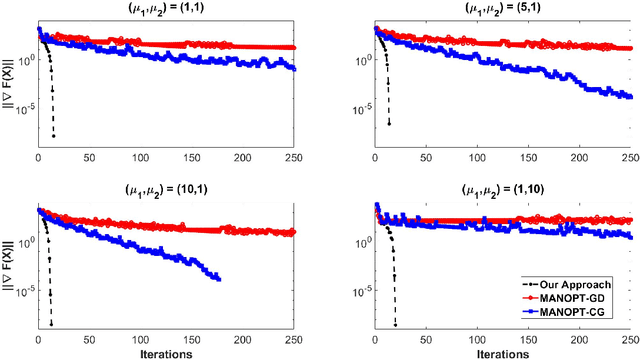
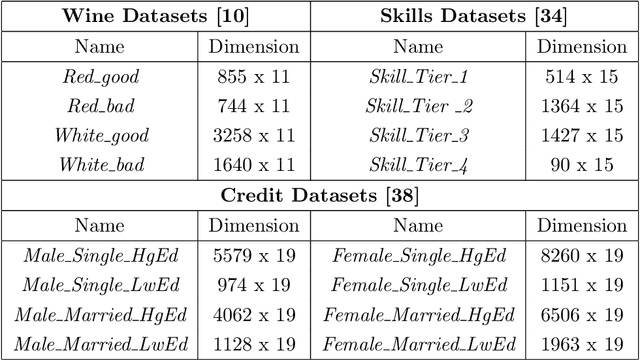
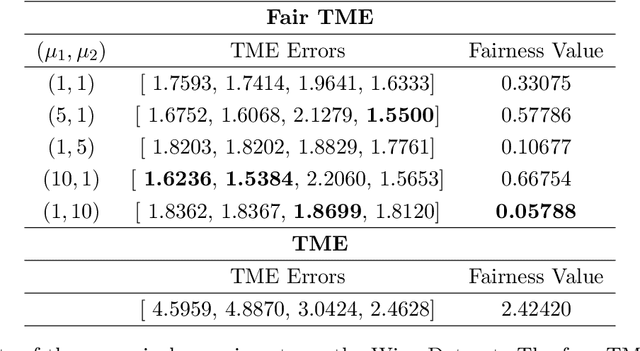
Matrix functions are utilized to rewrite smooth spectral constrained matrix optimization problems as smooth unconstrained problems over the set of symmetric matrices which are then solved via the cubic-regularized Newton method. A second-order chain rule identity for matrix functions is proven to compute the higher-order derivatives to implement cubic-regularized Newton, and a new convergence analysis is provided for cubic-regularized Newton for matrix vector spaces. We demonstrate the applicability of our approach by conducting numerical experiments on both synthetic and real datasets. In our experiments, we formulate a new model for estimating fair and robust covariance matrices in the spirit of the Tyler's M-estimator (TME) model and demonstrate its advantage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge