Lightweight Multi-Scale Feature Extraction with Fully Connected LMF Layer for Salient Object Detection

In the domain of computer vision, multi-scale feature extraction is vital for tasks such as salient object detection. However, achieving this capability in lightweight networks remains challenging due to the trade-off between efficiency and performance. This paper proposes a novel lightweight multi-scale feature extraction layer, termed the LMF layer, which employs depthwise separable dilated convolutions in a fully connected structure. By integrating multiple LMF layers, we develop LMFNet, a lightweight network tailored for salient object detection. Our approach significantly reduces the number of parameters while maintaining competitive performance. Here, we show that LMFNet achieves state-of-the-art or comparable results on five benchmark datasets with only 0.81M parameters, outperforming several traditional and lightweight models in terms of both efficiency and accuracy. Our work not only addresses the challenge of multi-scale learning in lightweight networks but also demonstrates the potential for broader applications in image processing tasks. The related code files are available at https://github.com/Shi-Yun-peng/LMFNet

Fast alignment of heterogeneous images in sliced Wasserstein distance

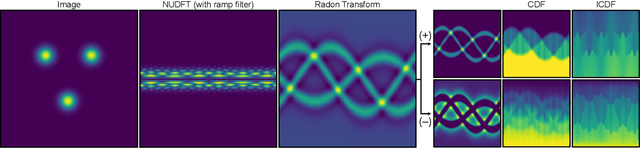
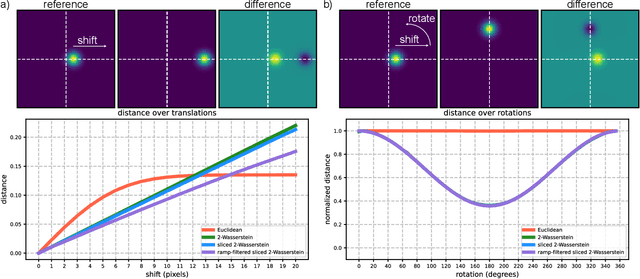
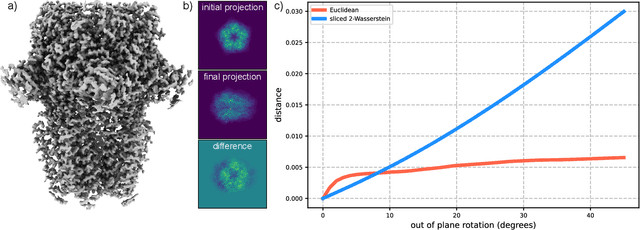
Many applications of computer vision rely on the alignment of similar but non-identical images. We present a fast algorithm for aligning heterogeneous images based on optimal transport. Our approach combines the speed of fast Fourier methods with the robustness of sliced probability metrics and allows us to efficiently compute the alignment between two $L \times L$ images using the sliced 2-Wasserstein distance in $O(L^2 \log L)$ operations. We show that our method is robust to translations, rotations and deformations in the images.

Efficient Detection of Long Consistent Cycles and its Application to Distributed Synchronization

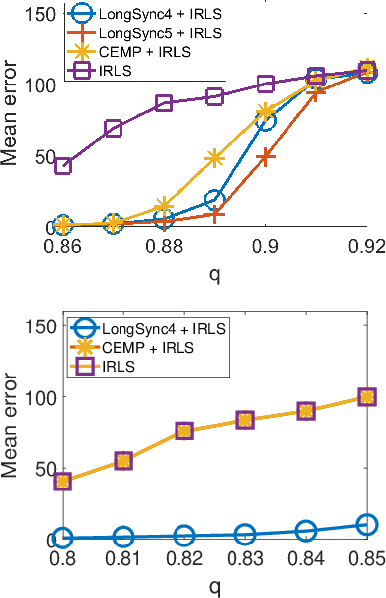
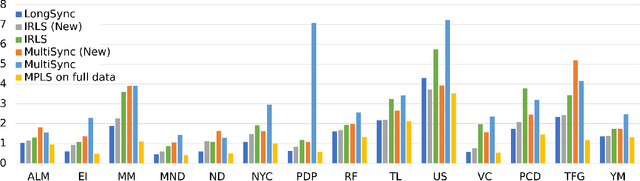
Group synchronization plays a crucial role in global pipelines for Structure from Motion (SfM). Its formulation is nonconvex and it is faced with highly corrupted measurements. Cycle consistency has been effective in addressing these challenges. However, computationally efficient solutions are needed for cycles longer than three, especially in practical scenarios where 3-cycles are unavailable. To overcome this computational bottleneck, we propose an algorithm for group synchronization that leverages information from cycles of lengths ranging from three to six with a time complexity of order $O(n^3)$ (or $O(n^{2.373})$ when using a faster matrix multiplication algorithm). We establish non-trivial theory for this and related methods that achieves competitive sample complexity, assuming the uniform corruption model. To advocate the practical need for our method, we consider distributed group synchronization, which requires at least 4-cycles, and we illustrate state-of-the-art performance by our method in this context.

Robust Group Synchronization via Quadratic Programming

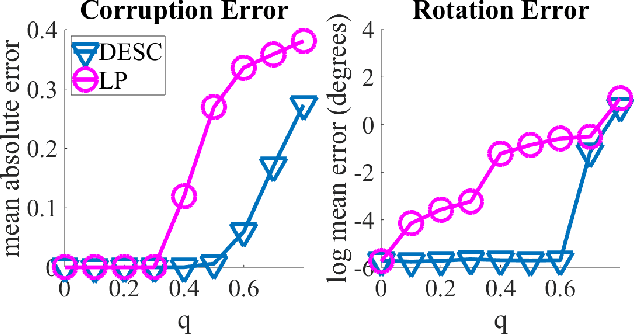
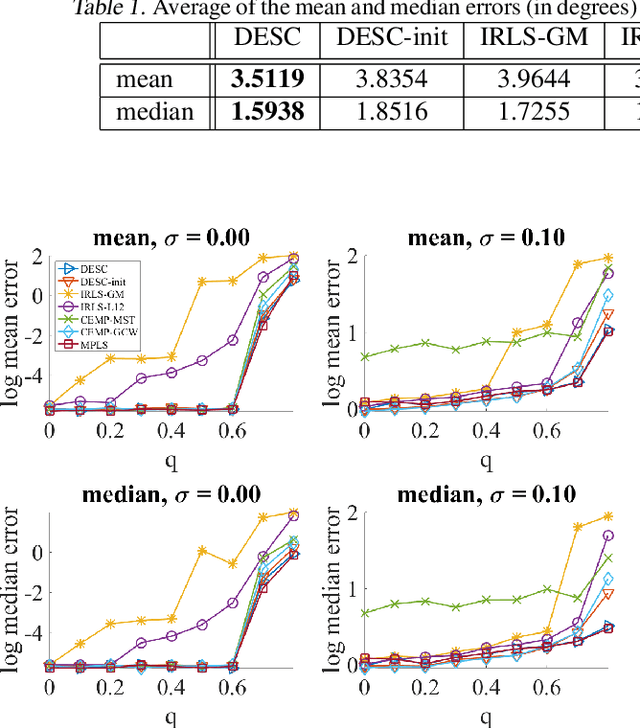
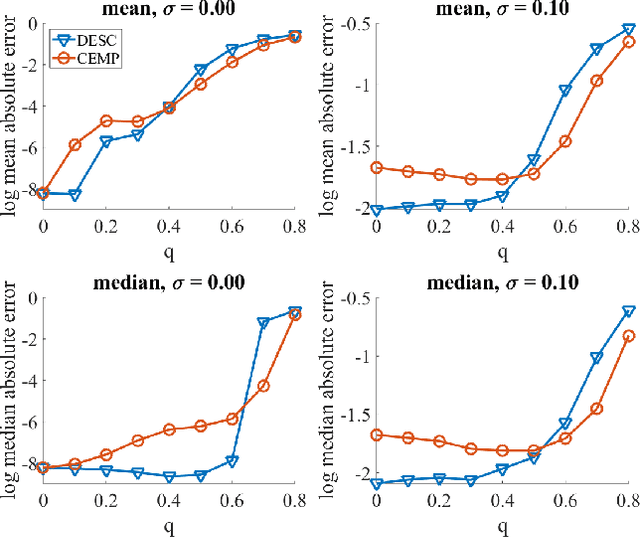
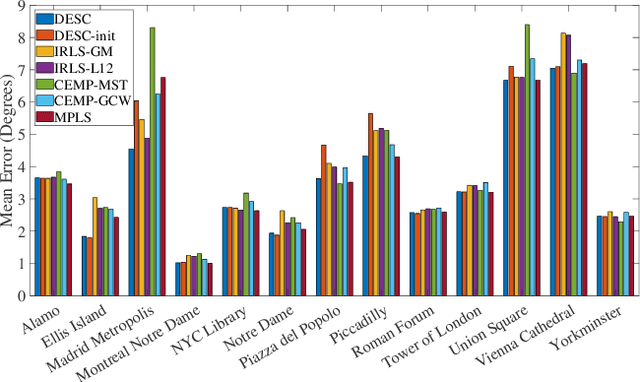
We propose a novel quadratic programming formulation for estimating the corruption levels in group synchronization, and use these estimates to solve this problem. Our objective function exploits the cycle consistency of the group and we thus refer to our method as detection and estimation of structural consistency (DESC). This general framework can be extended to other algebraic and geometric structures. Our formulation has the following advantages: it can tolerate corruption as high as the information-theoretic bound, it does not require a good initialization for the estimates of group elements, it has a simple interpretation, and under some mild conditions the global minimum of our objective function exactly recovers the corruption levels. We demonstrate the competitive accuracy of our approach on both synthetic and real data experiments of rotation averaging.

Fast, Accurate and Memory-Efficient Partial Permutation Synchronization

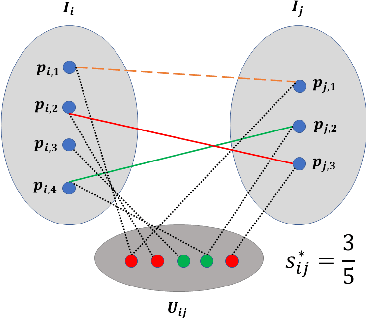
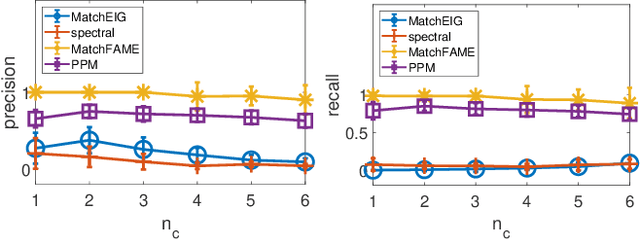
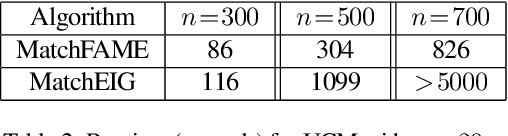
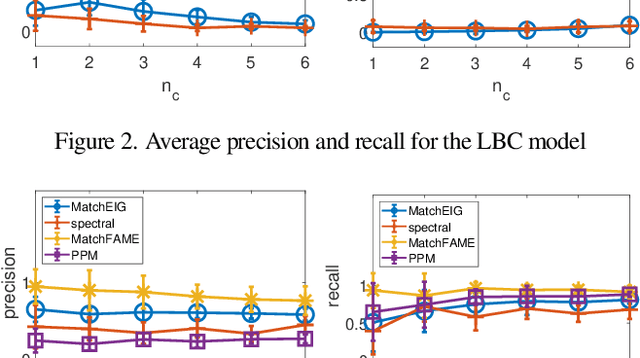
Previous partial permutation synchronization (PPS) algorithms, which are commonly used for multi-object matching, often involve computation-intensive and memory-demanding matrix operations. These operations become intractable for large scale structure-from-motion datasets. For pure permutation synchronization, the recent Cycle-Edge Message Passing (CEMP) framework suggests a memory-efficient and fast solution. Here we overcome the restriction of CEMP to compact groups and propose an improved algorithm, CEMP-Partial, for estimating the corruption levels of the observed partial permutations. It allows us to subsequently implement a nonconvex weighted projected power method without the need of spectral initialization. The resulting new PPS algorithm, MatchFAME (Fast, Accurate and Memory-Efficient Matching), only involves sparse matrix operations, and thus enjoys lower time and space complexities in comparison to previous PPS algorithms. We prove that under adversarial corruption, though without additive noise and with certain assumptions, CEMP-Partial is able to exactly classify corrupted and clean partial permutations. We demonstrate the state-of-the-art accuracy, speed and memory efficiency of our method on both synthetic and real datasets.

Ab-initio Contrast Estimation and Denoising of Cryo-EM Images

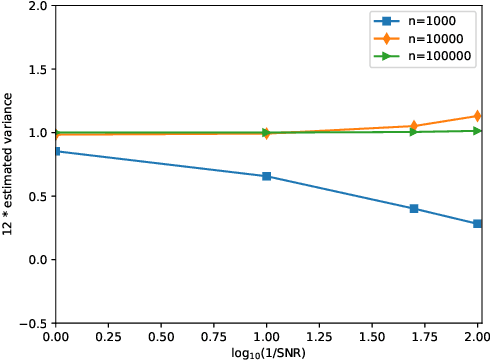
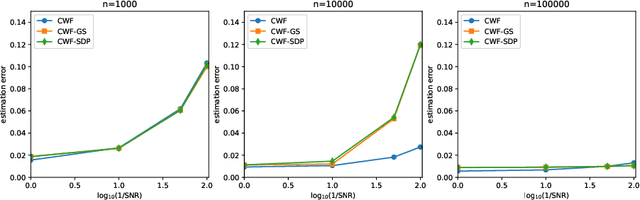
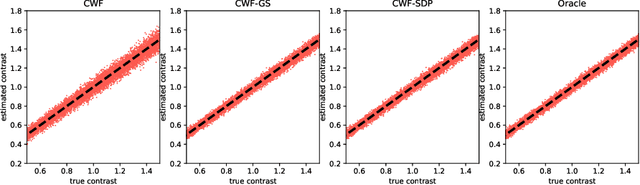
Background and Objective: The contrast of cryo-EM images vary from one to another, primarily due to the uneven thickness of ice layers. The variation of contrast can affect the quality of 2-D class averaging, 3-D ab-initio modeling, and 3-D heterogeneity analysis. Contrast estimation is currently performed during 3-D iterative refinement. As a result, the estimates are not available for class averaging and ab-initio modeling. However, these methods require good initial estimates of 3-D volumes and 3-D rotations of molecules. This paper aims to solve the contrast estimation problem in the ab-initio stage, without estimating the 3-D volume. Methods: The key observation underlying our analysis is that the 2-D covariance matrix of the raw images is related to the covariance of the underlying clean images, the noise variance, and the contrast variability between images. We show that the contrast variability can be derived from the 2-D covariance matrix and use the existing Covariance Wiener Filtering (CWF) framework to estimate it. We also demonstrate a modification of CWF to estimate the contrast of individual images. Results: Our method improves the contrast estimation by a large margin, compared to the previous CWF method. Its estimation accuracy is often comparable to that of an oracle that knows the ground truth covariance of the clean images. The more accurate contrast estimation also improves the quality of image denoising as demonstrated in both synthetic and experimental datasets. Conclusions: This paper proposes an effective method for contrast estimation directly from noisy images without using any 3-D volume information. It enables contrast correction in the earlier stage of single particle analysis, and may improve the accuracy of downstream processing.

Scalable Cluster-Consistency Statistics for Robust Multi-Object Matching

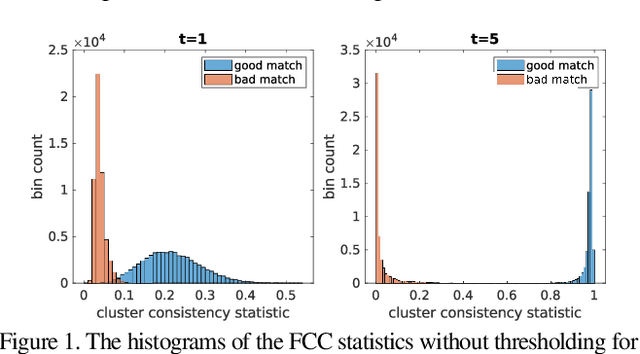
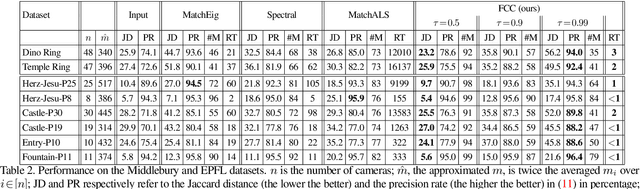
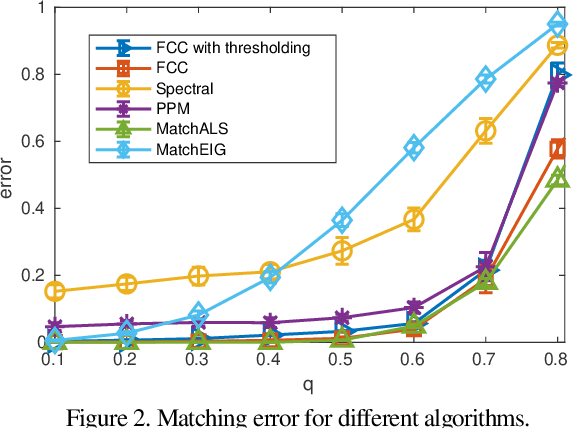
We develop new statistics for robustly filtering corrupted keypoint matches in the structure from motion pipeline. The statistics are based on consistency constraints that arise within the clustered structure of the graph of keypoint matches. The statistics are designed to give smaller values to corrupted matches and than uncorrupted matches. These new statistics are combined with an iterative reweighting scheme to filter keypoints, which can then be fed into any standard structure from motion pipeline. This filtering method can be efficiently implemented and scaled to massive datasets as it only requires sparse matrix multiplication. We demonstrate the efficacy of this method on synthetic and real structure from motion datasets and show that it achieves state-of-the-art accuracy and speed in these tasks.

Message Passing Least Squares Framework and its Application to Rotation Synchronization

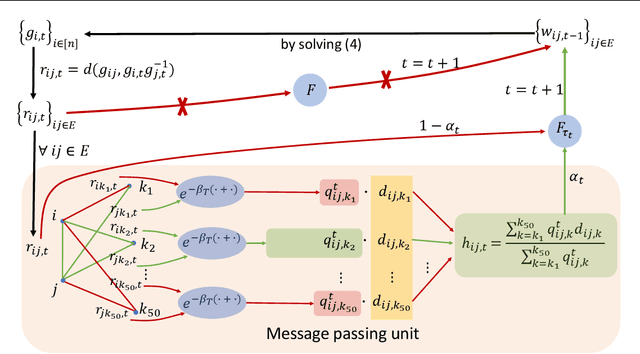
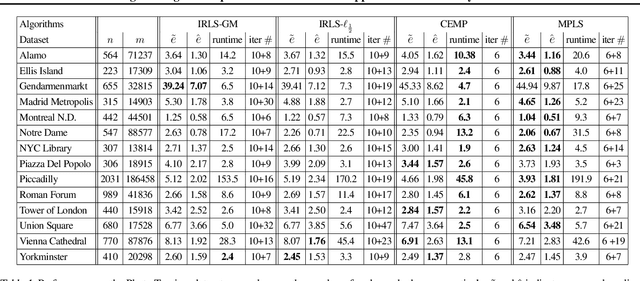
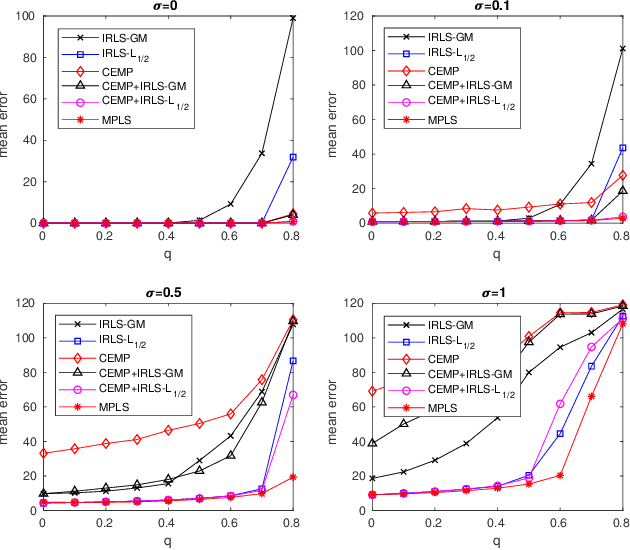
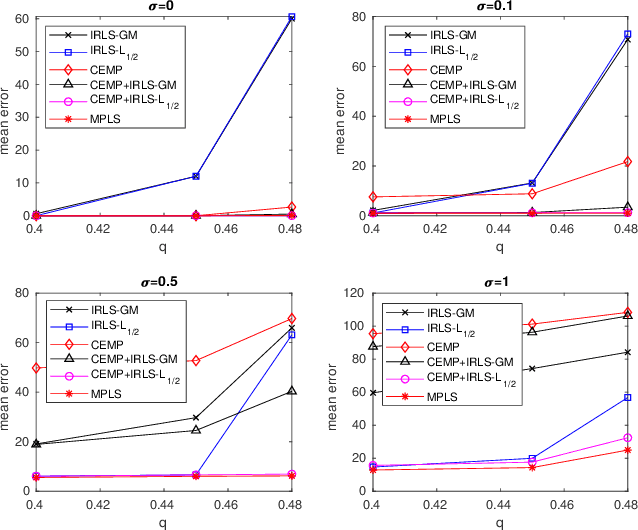
We propose an efficient algorithm for solving group synchronization under high levels of corruption and noise, while we focus on rotation synchronization. We first describe our recent theoretically guaranteed message passing algorithm that estimates the corruption levels of the measured group ratios. We then propose a novel reweighted least squares method to estimate the group elements, where the weights are initialized and iteratively updated using the estimated corruption levels. We demonstrate the superior performance of our algorithm over state-of-the-art methods for rotation synchronization using both synthetic and real data.

Robust Multi-object Matching via Iterative Reweighting of the Graph Connection Laplacian

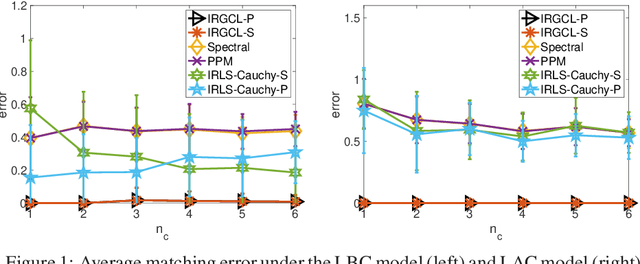
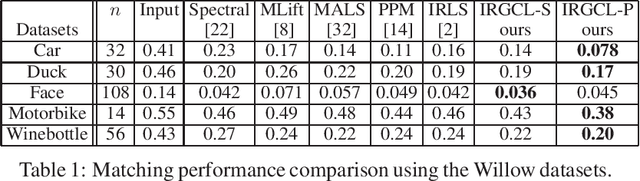
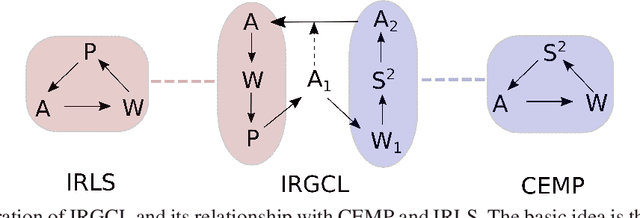
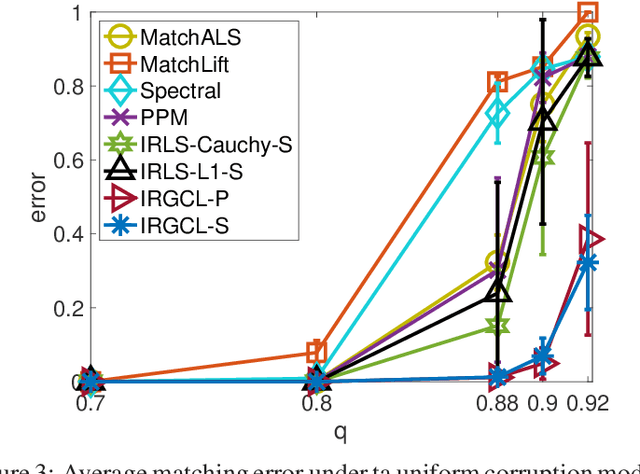
We propose an efficient and robust iterative solution to the multi-object matching problem. We first clarify serious limitations of current methods as well as the inappropriateness of the standard iteratively reweighted least squares procedure. In view of these limitations, we propose a novel and more reliable iterative reweighting strategy that incorporates information from higher-order neighborhoods by exploiting the graph connection Laplacian. We demonstrate the superior performance of our procedure over state-of-the-art methods using both synthetic and real datasets.

Robust Group Synchronization via Cycle-Edge Message Passing

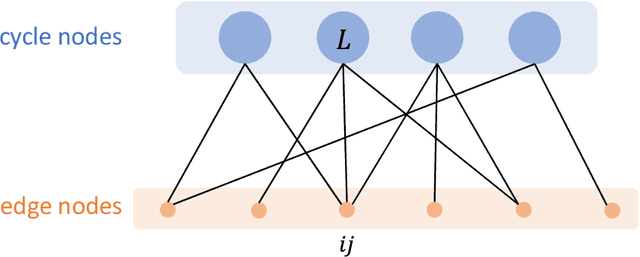
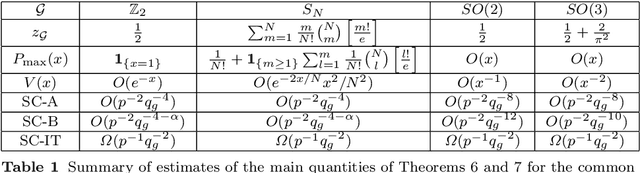
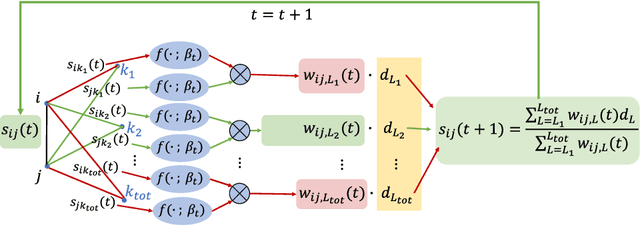
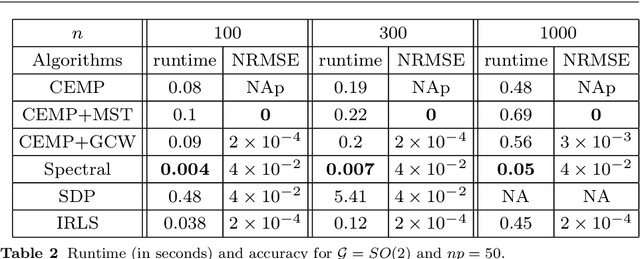
We propose a general framework for group synchronization with adversarial corruption and sufficiently small noise. Specifically, we apply a novel message passing procedure that uses cycle consistency information in order to estimate the corruption levels of group ratios and consequently infer the corrupted group ratios and solve the synchronization problem. We first explain why the group cycle consistency information is essential for effectively solving group synchronization problems. We then establish exact recovery and linear convergence guarantees for the proposed message passing procedure under a deterministic setting with adversarial corruption. These guarantees hold as long as the ratio of corrupted cycles per edge is bounded by a reasonable constant. We also establish the stability of the proposed procedure to sub-Gaussian noise. We further show that under a uniform corruption model, the recovery results are sharp in terms of an information-theoretic bound.