Robust Group Synchronization via Cycle-Edge Message Passing

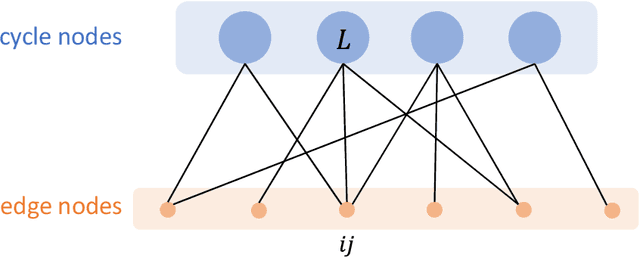
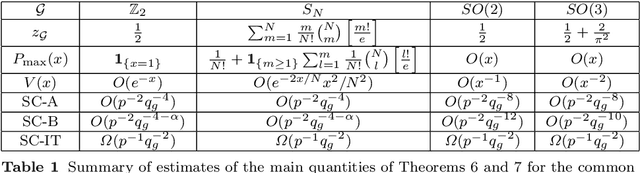
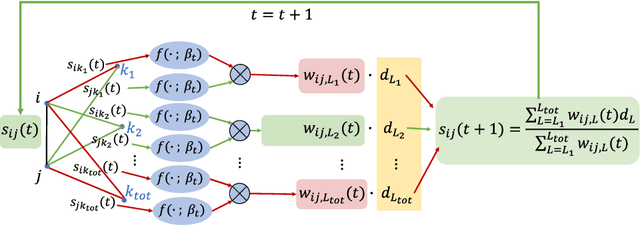
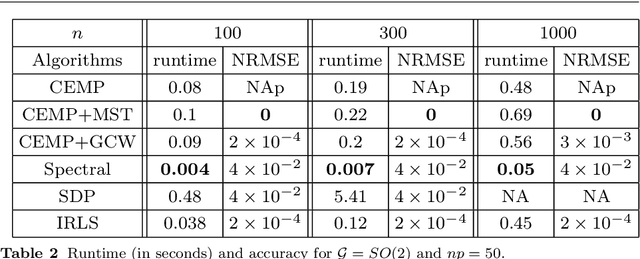
We propose a general framework for group synchronization with adversarial corruption and sufficiently small noise. Specifically, we apply a novel message passing procedure that uses cycle consistency information in order to estimate the corruption levels of group ratios and consequently infer the corrupted group ratios and solve the synchronization problem. We first explain why the group cycle consistency information is essential for effectively solving group synchronization problems. We then establish exact recovery and linear convergence guarantees for the proposed message passing procedure under a deterministic setting with adversarial corruption. These guarantees hold as long as the ratio of corrupted cycles per edge is bounded by a reasonable constant. We also establish the stability of the proposed procedure to sub-Gaussian noise. We further show that under a uniform corruption model, the recovery results are sharp in terms of an information-theoretic bound.