Diagonally-Weighted Generalized Method of Moments Estimation for Gaussian Mixture Modeling

Since Pearson [Philosophical Transactions of the Royal Society of London. A, 185 (1894), pp. 71-110] first applied the method of moments (MM) for modeling data as a mixture of one-dimensional Gaussians, moment-based estimation methods have proliferated. Among these methods, the generalized method of moments (GMM) improves the statistical efficiency of MM by weighting the moments appropriately. However, the computational complexity and storage complexity of MM and GMM grow exponentially with the dimension, making these methods impractical for high-dimensional data or when higher-order moments are required. Such computational bottlenecks are more severe in GMM since it additionally requires estimating a large weighting matrix. To overcome these bottlenecks, we propose the diagonally-weighted GMM (DGMM), which achieves a balance among statistical efficiency, computational complexity, and numerical stability. We apply DGMM to study the parameter estimation problem for weakly separated heteroscedastic low-rank Gaussian mixtures and design a computationally efficient and numerically stable algorithm that obtains the DGMM estimator without explicitly computing or storing the moment tensors. We implement the proposed algorithm and empirically validate the advantages of DGMM: in numerical studies, DGMM attains smaller estimation errors while requiring substantially shorter runtime than MM and GMM. The code and data will be available upon publication at https://github.com/liu-lzhang/dgmm.

Manifold learning in metric spaces

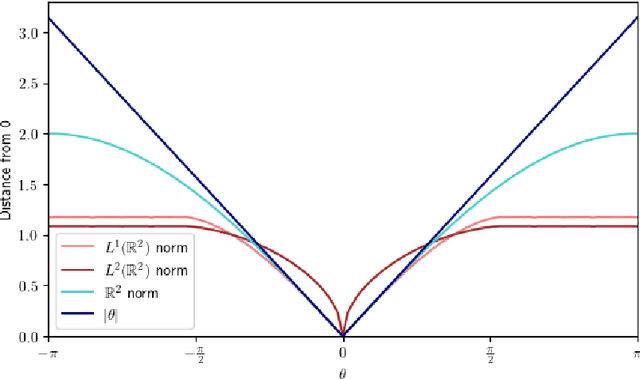
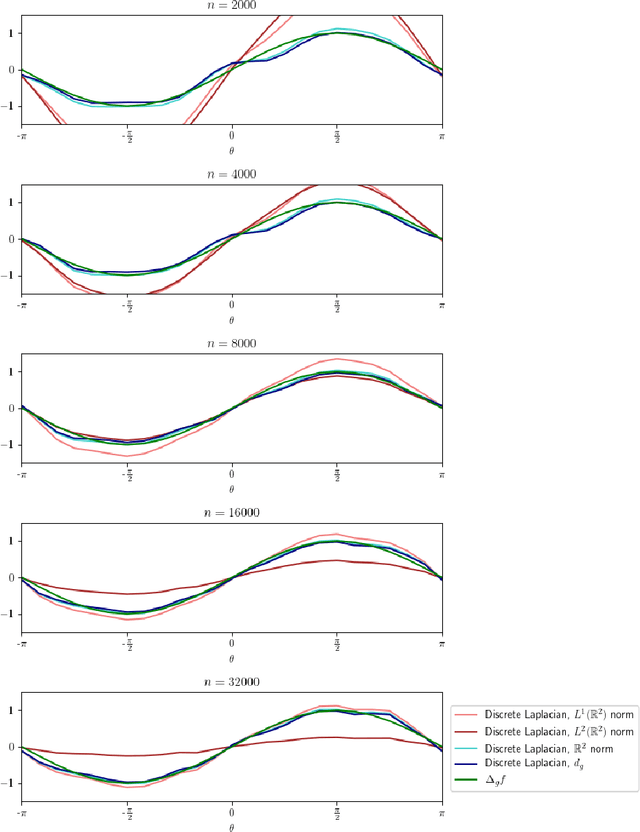
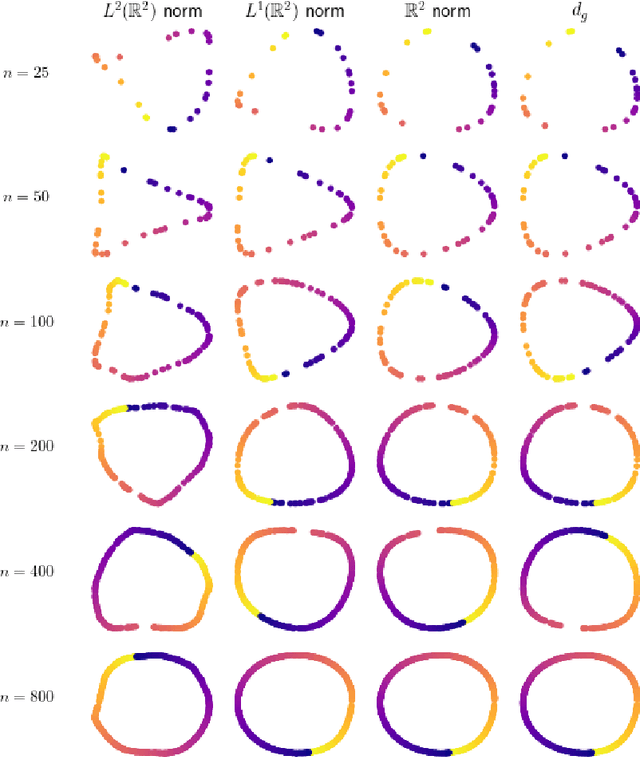
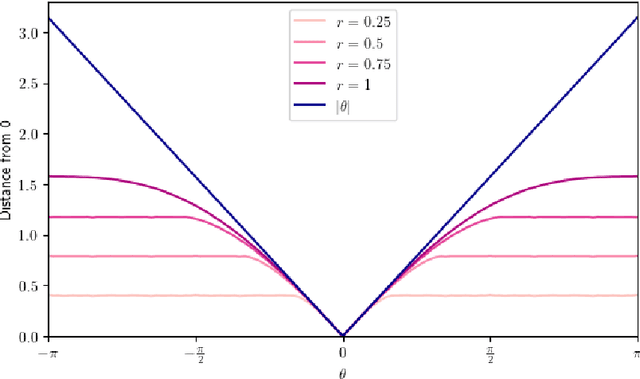
Laplacian-based methods are popular for dimensionality reduction of data lying in $\mathbb{R}^N$. Several theoretical results for these algorithms depend on the fact that the Euclidean distance approximates the geodesic distance on the underlying submanifold which the data are assumed to lie on. However, for some applications, other metrics, such as the Wasserstein distance, may provide a more appropriate notion of distance than the Euclidean distance. We provide a framework that generalizes the problem of manifold learning to metric spaces and study when a metric satisfies sufficient conditions for the pointwise convergence of the graph Laplacian.

Fast alignment of heterogeneous images in sliced Wasserstein distance

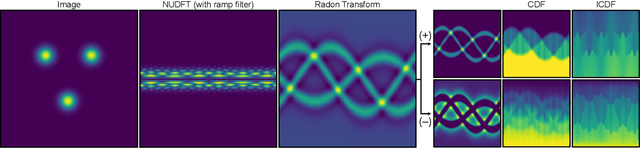
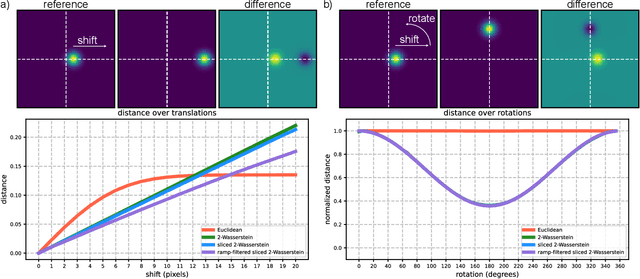
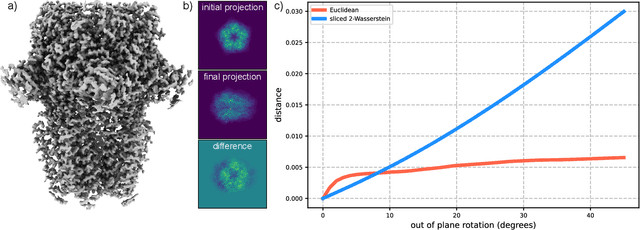
Many applications of computer vision rely on the alignment of similar but non-identical images. We present a fast algorithm for aligning heterogeneous images based on optimal transport. Our approach combines the speed of fast Fourier methods with the robustness of sliced probability metrics and allows us to efficiently compute the alignment between two $L \times L$ images using the sliced 2-Wasserstein distance in $O(L^2 \log L)$ operations. We show that our method is robust to translations, rotations and deformations in the images.

Moment-based metrics for molecules computable from cryo-EM images

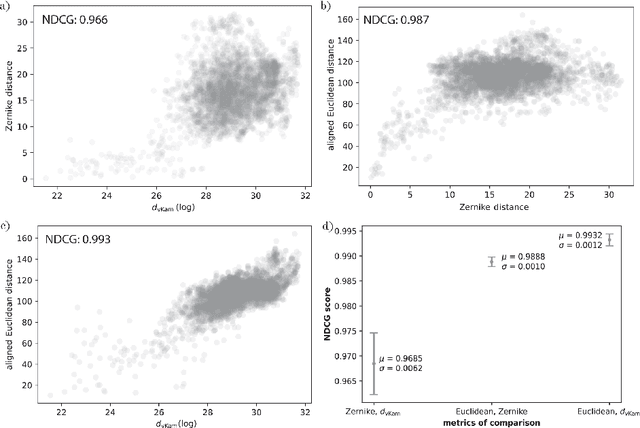
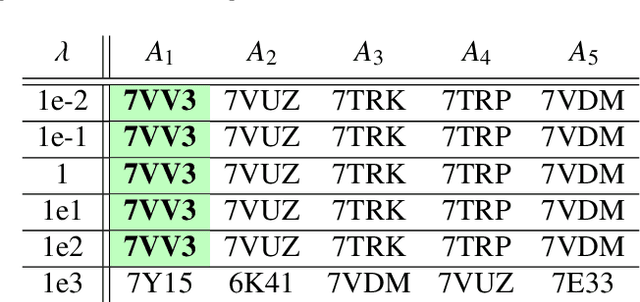
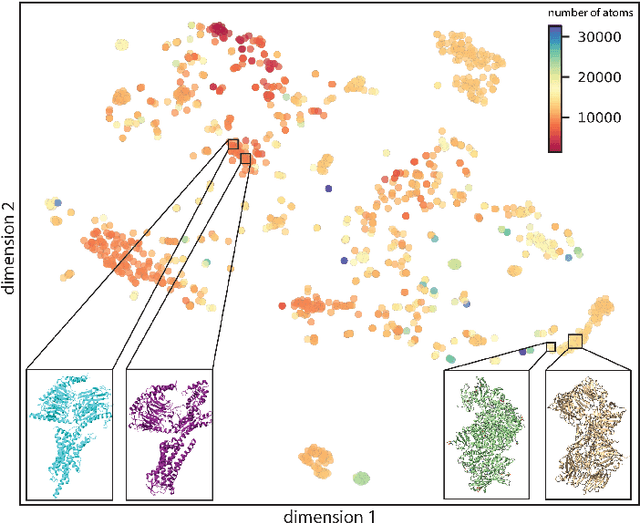
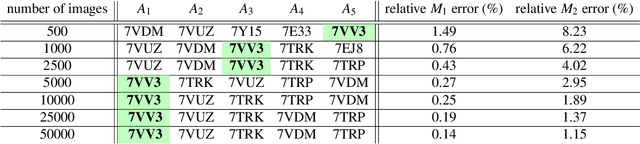
Single particle cryogenic electron microscopy (cryo-EM) is an imaging technique capable of recovering the high-resolution 3-D structure of biological macromolecules from many noisy and randomly oriented projection images. One notable approach to 3-D reconstruction, known as Kam's method, relies on the moments of the 2-D images. Inspired by Kam's method, we introduce a rotationally invariant metric between two molecular structures, which does not require 3-D alignment. Further, we introduce a metric between a stack of projection images and a molecular structure, which is invariant to rotations and reflections and does not require performing 3-D reconstruction. Additionally, the latter metric does not assume a uniform distribution of viewing angles. We demonstrate uses of the new metrics on synthetic and experimental datasets, highlighting their ability to measure structural similarity.

Alignment of Density Maps in Wasserstein Distance

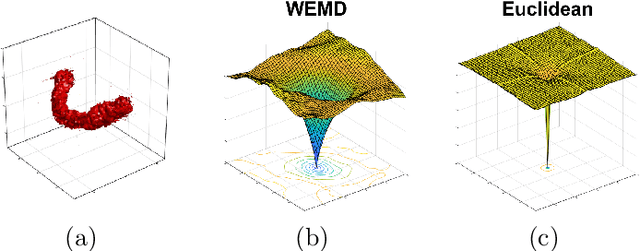
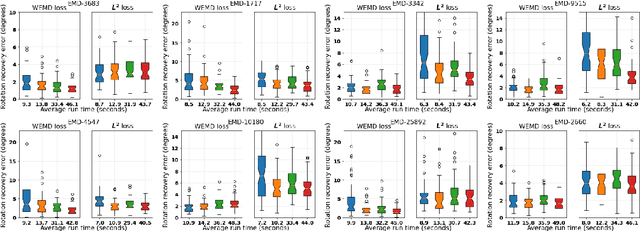
In this paper we propose an algorithm for aligning three-dimensional objects when represented as density maps, motivated by applications in cryogenic electron microscopy. The algorithm is based on minimizing the 1-Wasserstein distance between the density maps after a rigid transformation. The induced loss function enjoys a more benign landscape than its Euclidean counterpart and Bayesian optimization is employed for computation. Numerical experiments show improved accuracy and efficiency over existing algorithms on the alignment of real protein molecules. In the context of aligning heterogeneous pairs, we illustrate a potential need for new distance functions.

A stochastic approximate expectation-maximization for structure determination directly from cryo-EM micrographs

A single-particle cryo-electron microscopy (cryo-EM) measurement, called a micrograph, consists of multiple two-dimensional tomographic projections of a three-dimensional molecular structure at unknown locations, taken under unknown viewing directions. All existing cryo-EM algorithmic pipelines first locate and extract the projection images, and then reconstruct the structure from the extracted images. However, if the molecular structure is small, the signal-to-noise ratio (SNR) of the data is very low, and thus accurate detection of projection images within the micrograph is challenging. Consequently, all standard techniques fail in low-SNR regimes. To recover molecular structures from measurements of low SNR, and in particular small molecular structures, we devise a stochastic approximate expectation-maximization algorithm to estimate the three-dimensional structure directly from the micrograph, bypassing locating the projection images. We corroborate our computational scheme with numerical experiments, and present successful structure recoveries from simulated noisy measurements.

Fast expansion into harmonics on the disk: a steerable basis with fast radial convolutions

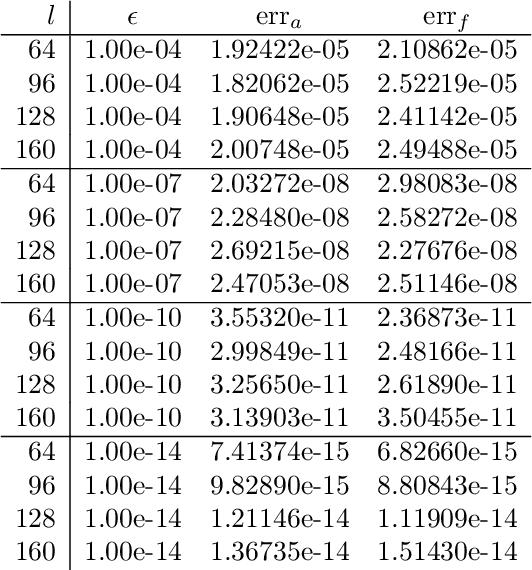
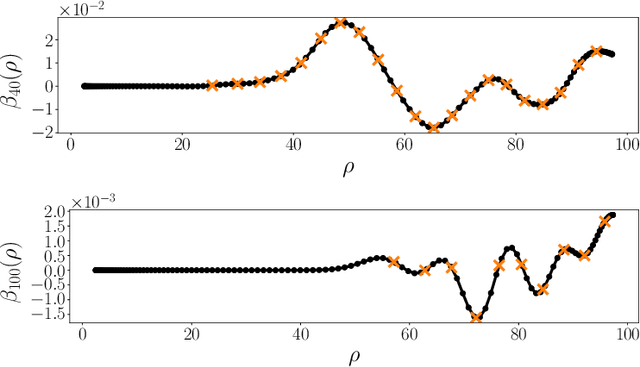
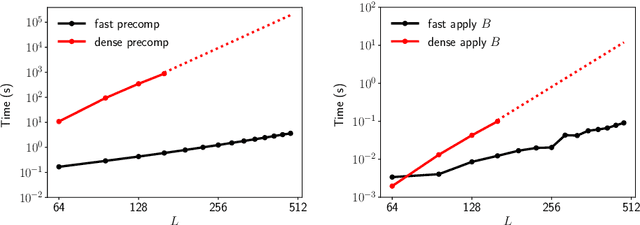
We present a fast and numerically accurate method for expanding digitized $L \times L$ images representing functions on $[-1,1]^2$ supported on the disk $\{x \in \mathbb{R}^2 : |x|<1\}$ in the harmonics (Dirichlet Laplacian eigenfunctions) on the disk. Our method runs in $\mathcal{O}(L^2 \log L)$ operations. This basis is also known as the Fourier-Bessel basis and it has several computational advantages: it is orthogonal, ordered by frequency, and steerable in the sense that images expanded in the basis can be rotated by applying a diagonal transform to the coefficients. Moreover, we show that convolution with radial functions can also be efficiently computed by applying a diagonal transform to the coefficients.

A Molecular Prior Distribution for Bayesian Inference Based on Wilson Statistics

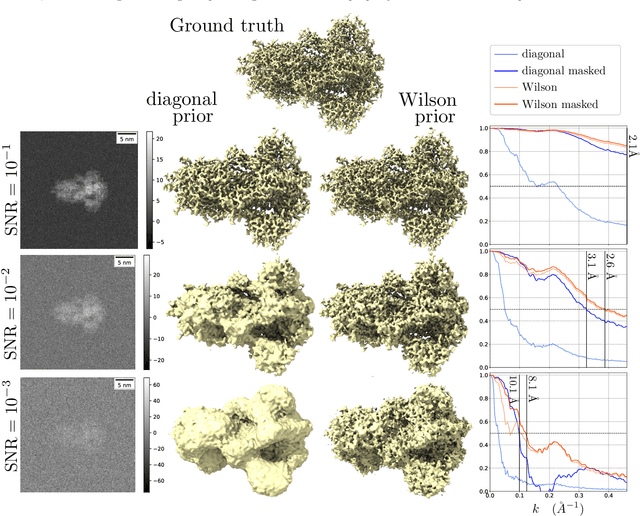
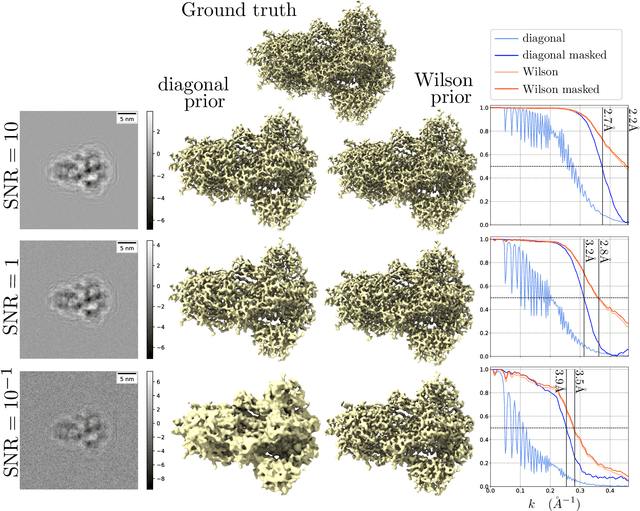
Background and Objective: Wilson statistics describe well the power spectrum of proteins at high frequencies. Therefore, it has found several applications in structural biology, e.g., it is the basis for sharpening steps used in cryogenic electron microscopy (cryo-EM). A recent paper gave the first rigorous proof of Wilson statistics based on a formalism of Wilson's original argument. This new analysis also leads to statistical estimates of the scattering potential of proteins that reveal a correlation between neighboring Fourier coefficients. Here we exploit these estimates to craft a novel prior that can be used for Bayesian inference of molecular structures. Methods: We describe the properties of the prior and the computation of its hyperparameters. We then evaluate the prior on two synthetic linear inverse problems, and compare against a popular prior in cryo-EM reconstruction at a range of SNRs. Results: We show that the new prior effectively suppresses noise and fills-in low SNR regions in the spectral domain. Furthermore, it improves the resolution of estimates on the problems considered for a wide range of SNR and produces Fourier Shell Correlation curves that are insensitive to masking effects. Conclusions: We analyze the assumptions in the model, discuss relations to other regularization strategies, and postulate on potential implications for structure determination in cryo-EM.

Ab-initio Contrast Estimation and Denoising of Cryo-EM Images

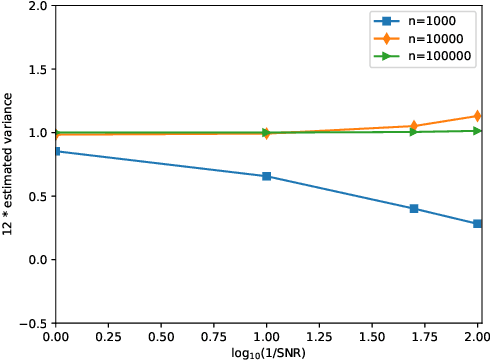
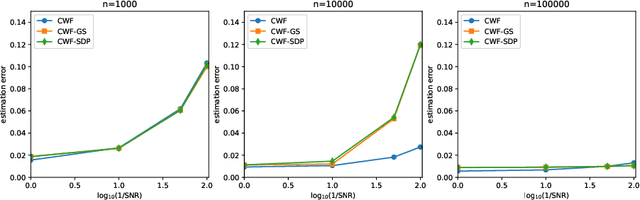
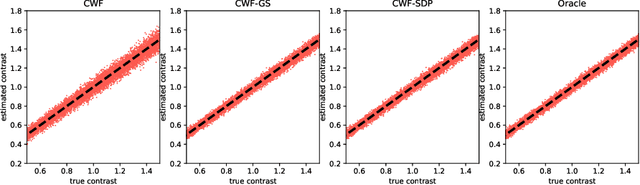
Background and Objective: The contrast of cryo-EM images vary from one to another, primarily due to the uneven thickness of ice layers. The variation of contrast can affect the quality of 2-D class averaging, 3-D ab-initio modeling, and 3-D heterogeneity analysis. Contrast estimation is currently performed during 3-D iterative refinement. As a result, the estimates are not available for class averaging and ab-initio modeling. However, these methods require good initial estimates of 3-D volumes and 3-D rotations of molecules. This paper aims to solve the contrast estimation problem in the ab-initio stage, without estimating the 3-D volume. Methods: The key observation underlying our analysis is that the 2-D covariance matrix of the raw images is related to the covariance of the underlying clean images, the noise variance, and the contrast variability between images. We show that the contrast variability can be derived from the 2-D covariance matrix and use the existing Covariance Wiener Filtering (CWF) framework to estimate it. We also demonstrate a modification of CWF to estimate the contrast of individual images. Results: Our method improves the contrast estimation by a large margin, compared to the previous CWF method. Its estimation accuracy is often comparable to that of an oracle that knows the ground truth covariance of the clean images. The more accurate contrast estimation also improves the quality of image denoising as demonstrated in both synthetic and experimental datasets. Conclusions: This paper proposes an effective method for contrast estimation directly from noisy images without using any 3-D volume information. It enables contrast correction in the earlier stage of single particle analysis, and may improve the accuracy of downstream processing.

An approximate expectation-maximization for two-dimensional multi-target detection

We consider the two-dimensional multi-target detection (MTD) problem of estimating a target image from a noisy measurement that contains multiple copies of the image, each randomly rotated and translated. The MTD model serves as a mathematical abstraction of the structure reconstruction problem in single-particle cryo-electron microscopy, the chief motivation of this study. We focus on high noise regimes, where accurate detection of image occurrences within a measurement is impossible. To estimate the image, we develop an expectation-maximization framework that aims to maximize an approximation of the likelihood function. We demonstrate image recovery in highly noisy environments, and show that our framework outperforms the previously studied autocorrelation analysis in a wide range of parameters. The code to reproduce all numerical experiments is publicly available at https://github.com/krshay/MTD-2D-EM.