Bayesian Optimization on Networks

This paper studies optimization on networks modeled as metric graphs. Motivated by applications where the objective function is expensive to evaluate or only available as a black box, we develop Bayesian optimization algorithms that sequentially update a Gaussian process surrogate model of the objective to guide the acquisition of query points. To ensure that the surrogates are tailored to the network's geometry, we adopt Whittle-Mat\'ern Gaussian process prior models defined via stochastic partial differential equations on metric graphs. In addition to establishing regret bounds for optimizing sufficiently smooth objective functions, we analyze the practical case in which the smoothness of the objective is unknown and the Whittle-Mat\'ern prior is represented using finite elements. Numerical results demonstrate the effectiveness of our algorithms for optimizing benchmark objective functions on a synthetic metric graph and for Bayesian inversion via maximum a posteriori estimation on a telecommunication network.

Hierarchical Sequence Iteration for Heterogeneous Question Answering

Retrieval-augmented generation (RAG) remains brittle on multi-step questions and heterogeneous evidence sources, trading accuracy against latency and token/tool budgets. This paper introducesHierarchical Sequence (HSEQ) Iteration for Heterogeneous Question Answering, a unified framework that (i) linearize documents, tables, and knowledge graphs into a reversible hierarchical sequence with lightweight structural tags, and (ii) perform structure-aware iteration to collect just-enough evidence before answer synthesis. A Head Agent provides guidance that leads retrieval, while an Iteration Agent selects and expands HSeq via structure-respecting actions (e.g., parent/child hops, table row/column neighbors, KG relations); Finally the head agent composes canonicalized evidence to genearte the final answer, with an optional refinement loop to resolve detected contradictions. Experiments on HotpotQA (text), HybridQA/TAT-QA (table+text), and MetaQA (KG) show consistent EM/F1 gains over strong single-pass, multi-hop, and agentic RAG baselines with high efficiency. Besides, HSEQ exhibits three key advantages: (1) a format-agnostic unification that enables a single policy to operate across text, tables, and KGs without per-dataset specialization; (2) guided, budget-aware iteration that reduces unnecessary hops, tool calls, and tokens while preserving accuracy; and (3) evidence canonicalization for reliable QA, improving answers consistency and auditability.

Divide by Question, Conquer by Agent: SPLIT-RAG with Question-Driven Graph Partitioning

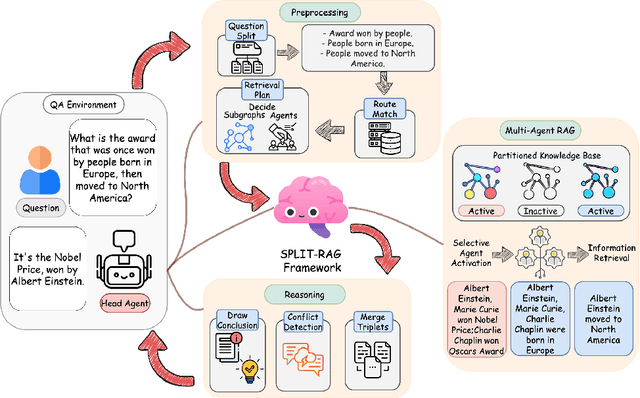
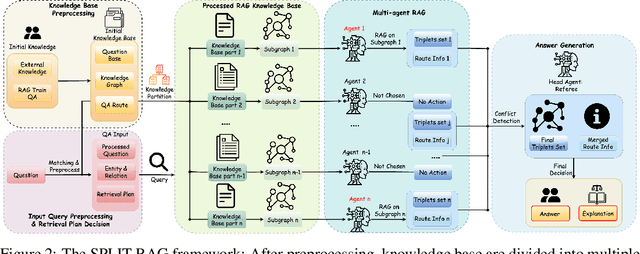
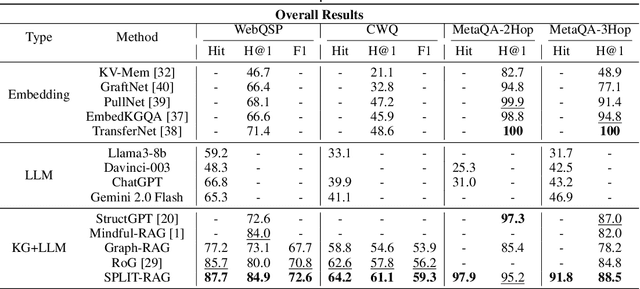
Retrieval-Augmented Generation (RAG) systems empower large language models (LLMs) with external knowledge, yet struggle with efficiency-accuracy trade-offs when scaling to large knowledge graphs. Existing approaches often rely on monolithic graph retrieval, incurring unnecessary latency for simple queries and fragmented reasoning for complex multi-hop questions. To address these challenges, this paper propose SPLIT-RAG, a multi-agent RAG framework that addresses these limitations with question-driven semantic graph partitioning and collaborative subgraph retrieval. The innovative framework first create Semantic Partitioning of Linked Information, then use the Type-Specialized knowledge base to achieve Multi-Agent RAG. The attribute-aware graph segmentation manages to divide knowledge graphs into semantically coherent subgraphs, ensuring subgraphs align with different query types, while lightweight LLM agents are assigned to partitioned subgraphs, and only relevant partitions are activated during retrieval, thus reduce search space while enhancing efficiency. Finally, a hierarchical merging module resolves inconsistencies across subgraph-derived answers through logical verifications. Extensive experimental validation demonstrates considerable improvements compared to existing approaches.

KG-IRAG: A Knowledge Graph-Based Iterative Retrieval-Augmented Generation Framework for Temporal Reasoning

Graph Retrieval-Augmented Generation (GraphRAG) has proven highly effective in enhancing the performance of Large Language Models (LLMs) on tasks that require external knowledge. By leveraging Knowledge Graphs (KGs), GraphRAG improves information retrieval for complex reasoning tasks, providing more precise and comprehensive retrieval and generating more accurate responses to QAs. However, most RAG methods fall short in addressing multi-step reasoning, particularly when both information extraction and inference are necessary. To address this limitation, this paper presents Knowledge Graph-Based Iterative Retrieval-Augmented Generation (KG-IRAG), a novel framework that integrates KGs with iterative reasoning to improve LLMs' ability to handle queries involving temporal and logical dependencies. Through iterative retrieval steps, KG-IRAG incrementally gathers relevant data from external KGs, enabling step-by-step reasoning. The proposed approach is particularly suited for scenarios where reasoning is required alongside dynamic temporal data extraction, such as determining optimal travel times based on weather conditions or traffic patterns. Experimental results show that KG-IRAG improves accuracy in complex reasoning tasks by effectively integrating external knowledge with iterative, logic-based retrieval. Additionally, three new datasets: weatherQA-Irish, weatherQA-Sydney, and trafficQA-TFNSW, are formed to evaluate KG-IRAG's performance, demonstrating its potential beyond traditional RAG applications.

Model-free Estimation of Latent Structure via Multiscale Nonparametric Maximum Likelihood

Multivariate distributions often carry latent structures that are difficult to identify and estimate, and which better reflect the data generating mechanism than extrinsic structures exhibited simply by the raw data. In this paper, we propose a model-free approach for estimating such latent structures whenever they are present, without assuming they exist a priori. Given an arbitrary density $p_0$, we construct a multiscale representation of the density and propose data-driven methods for selecting representative models that capture meaningful discrete structure. Our approach uses a nonparametric maximum likelihood estimator to estimate the latent structure at different scales and we further characterize their asymptotic limits. By carrying out such a multiscale analysis, we obtain coarseto-fine structures inherent in the original distribution, which are integrated via a model selection procedure to yield an interpretable discrete representation of it. As an application, we design a clustering algorithm based on the proposed procedure and demonstrate its effectiveness in capturing a wide range of latent structures.

SSTKG: Simple Spatio-Temporal Knowledge Graph for Intepretable and Versatile Dynamic Information Embedding

Knowledge graphs (KGs) have been increasingly employed for link prediction and recommendation using real-world datasets. However, the majority of current methods rely on static data, neglecting the dynamic nature and the hidden spatio-temporal attributes of real-world scenarios. This often results in suboptimal predictions and recommendations. Although there are effective spatio-temporal inference methods, they face challenges such as scalability with large datasets and inadequate semantic understanding, which impede their performance. To address these limitations, this paper introduces a novel framework - Simple Spatio-Temporal Knowledge Graph (SSTKG), for constructing and exploring spatio-temporal KGs. To integrate spatial and temporal data into KGs, our framework exploited through a new 3-step embedding method. Output embeddings can be used for future temporal sequence prediction and spatial information recommendation, providing valuable insights for various applications such as retail sales forecasting and traffic volume prediction. Our framework offers a simple but comprehensive way to understand the underlying patterns and trends in dynamic KG, thereby enhancing the accuracy of predictions and the relevance of recommendations. This work paves the way for more effective utilization of spatio-temporal data in KGs, with potential impacts across a wide range of sectors.

Gaussian Process Regression under Computational and Epistemic Misspecification

Gaussian process regression is a classical kernel method for function estimation and data interpolation. In large data applications, computational costs can be reduced using low-rank or sparse approximations of the kernel. This paper investigates the effect of such kernel approximations on the interpolation error. We introduce a unified framework to analyze Gaussian process regression under important classes of computational misspecification: Karhunen-Lo\`eve expansions that result in low-rank kernel approximations, multiscale wavelet expansions that induce sparsity in the covariance matrix, and finite element representations that induce sparsity in the precision matrix. Our theory also accounts for epistemic misspecification in the choice of kernel parameters.

Alignment of Density Maps in Wasserstein Distance

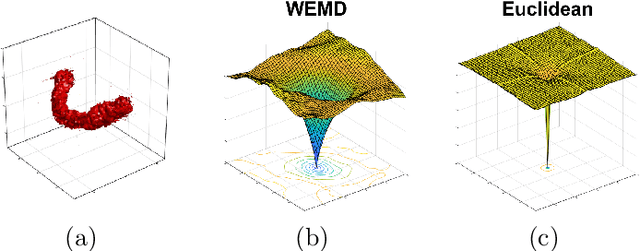
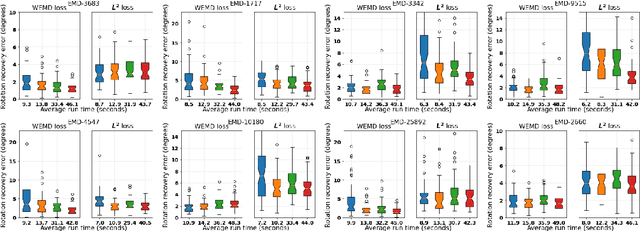
In this paper we propose an algorithm for aligning three-dimensional objects when represented as density maps, motivated by applications in cryogenic electron microscopy. The algorithm is based on minimizing the 1-Wasserstein distance between the density maps after a rigid transformation. The induced loss function enjoys a more benign landscape than its Euclidean counterpart and Bayesian optimization is employed for computation. Numerical experiments show improved accuracy and efficiency over existing algorithms on the alignment of real protein molecules. In the context of aligning heterogeneous pairs, we illustrate a potential need for new distance functions.

Mathematical Foundations of Graph-Based Bayesian Semi-Supervised Learning

In recent decades, science and engineering have been revolutionized by a momentous growth in the amount of available data. However, despite the unprecedented ease with which data are now collected and stored, labeling data by supplementing each feature with an informative tag remains to be challenging. Illustrative tasks where the labeling process requires expert knowledge or is tedious and time-consuming include labeling X-rays with a diagnosis, protein sequences with a protein type, texts by their topic, tweets by their sentiment, or videos by their genre. In these and numerous other examples, only a few features may be manually labeled due to cost and time constraints. How can we best propagate label information from a small number of expensive labeled features to a vast number of unlabeled ones? This is the question addressed by semi-supervised learning (SSL). This article overviews recent foundational developments on graph-based Bayesian SSL, a probabilistic framework for label propagation using similarities between features. SSL is an active research area and a thorough review of the extant literature is beyond the scope of this article. Our focus will be on topics drawn from our own research that illustrate the wide range of mathematical tools and ideas that underlie the rigorous study of the statistical accuracy and computational efficiency of graph-based Bayesian SSL.

Uniform Consistency in Nonparametric Mixture Models

We study uniform consistency in nonparametric mixture models as well as closely related mixture of regression (also known as mixed regression) models, where the regression functions are allowed to be nonparametric and the error distributions are assumed to be convolutions of a Gaussian density. We construct uniformly consistent estimators under general conditions while simultaneously highlighting several pain points in extending existing pointwise consistency results to uniform results. The resulting analysis turns out to be nontrivial, and several novel technical tools are developed along the way. In the case of mixed regression, we prove $L^1$ convergence of the regression functions while allowing for the component regression functions to intersect arbitrarily often, which presents additional technical challenges. We also consider generalizations to general (i.e. non-convolutional) nonparametric mixtures.