Fast expansion into harmonics on the disk: a steerable basis with fast radial convolutions
Paper and Code
Jul 27, 2022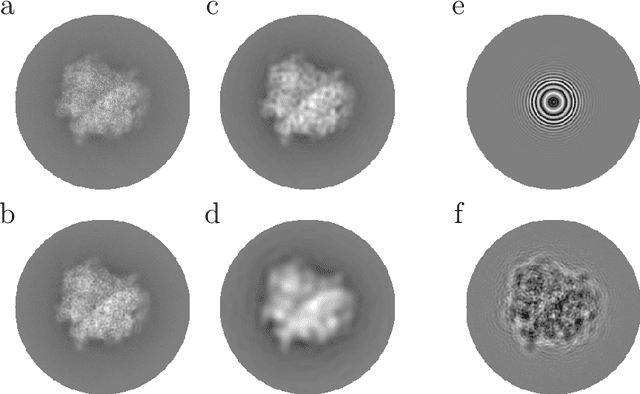
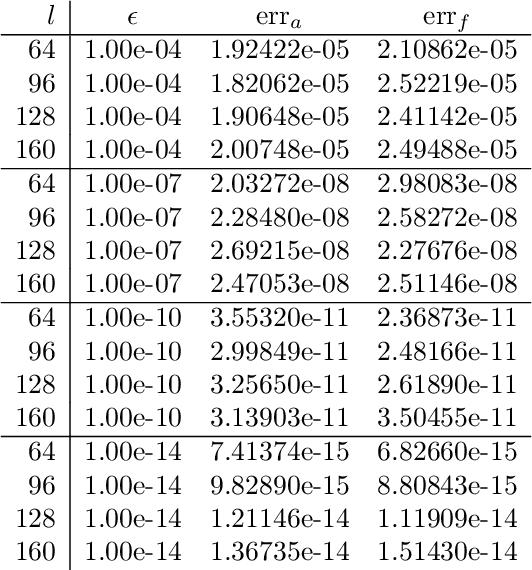
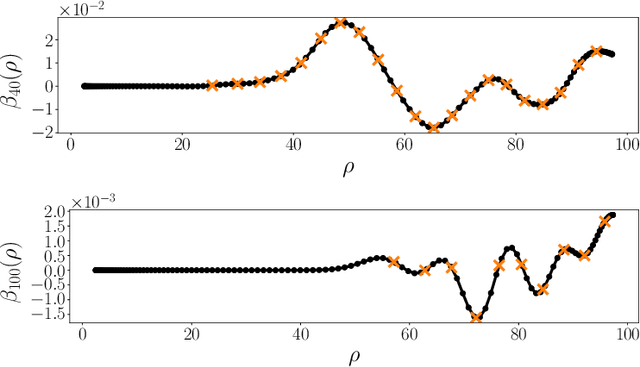
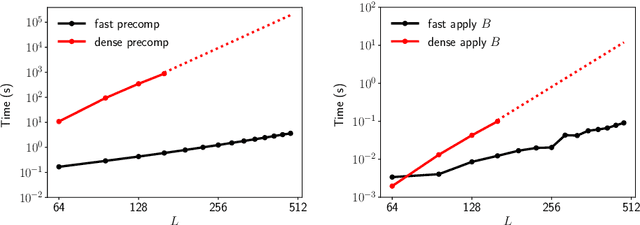
We present a fast and numerically accurate method for expanding digitized $L \times L$ images representing functions on $[-1,1]^2$ supported on the disk $\{x \in \mathbb{R}^2 : |x|<1\}$ in the harmonics (Dirichlet Laplacian eigenfunctions) on the disk. Our method runs in $\mathcal{O}(L^2 \log L)$ operations. This basis is also known as the Fourier-Bessel basis and it has several computational advantages: it is orthogonal, ordered by frequency, and steerable in the sense that images expanded in the basis can be rotated by applying a diagonal transform to the coefficients. Moreover, we show that convolution with radial functions can also be efficiently computed by applying a diagonal transform to the coefficients.
* 19 pages, 4 figures, 1 table
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge