Diagonally-Weighted Generalized Method of Moments Estimation for Gaussian Mixture Modeling

Since Pearson [Philosophical Transactions of the Royal Society of London. A, 185 (1894), pp. 71-110] first applied the method of moments (MM) for modeling data as a mixture of one-dimensional Gaussians, moment-based estimation methods have proliferated. Among these methods, the generalized method of moments (GMM) improves the statistical efficiency of MM by weighting the moments appropriately. However, the computational complexity and storage complexity of MM and GMM grow exponentially with the dimension, making these methods impractical for high-dimensional data or when higher-order moments are required. Such computational bottlenecks are more severe in GMM since it additionally requires estimating a large weighting matrix. To overcome these bottlenecks, we propose the diagonally-weighted GMM (DGMM), which achieves a balance among statistical efficiency, computational complexity, and numerical stability. We apply DGMM to study the parameter estimation problem for weakly separated heteroscedastic low-rank Gaussian mixtures and design a computationally efficient and numerically stable algorithm that obtains the DGMM estimator without explicitly computing or storing the moment tensors. We implement the proposed algorithm and empirically validate the advantages of DGMM: in numerical studies, DGMM attains smaller estimation errors while requiring substantially shorter runtime than MM and GMM. The code and data will be available upon publication at https://github.com/liu-lzhang/dgmm.

The beltway problem over orthogonal groups

The classical beltway problem entails recovering a set of points from their unordered pairwise distances on the circle. This problem can be viewed as a special case of the crystallographic phase retrieval problem of recovering a sparse signal from its periodic autocorrelation. Based on this interpretation, and motivated by cryo-electron microscopy, we suggest a natural generalization to orthogonal groups: recovering a sparse signal, up to an orthogonal transformation, from its autocorrelation over the orthogonal group. If the support of the signal is collision-free, we bound the number of solutions to the beltway problem over orthogonal groups, and prove that this bound is exactly one when the support of the signal is radially collision-free (i.e., the support points have distinct magnitudes). We also prove that if the pairwise products of the signal's weights are distinct, then the autocorrelation determines the signal uniquely, up to an orthogonal transformation. We conclude the paper by considering binary signals and show that in this case, the collision-free condition need not be sufficient to determine signals up to orthogonal transformation.

Moment-based metrics for molecules computable from cryo-EM images

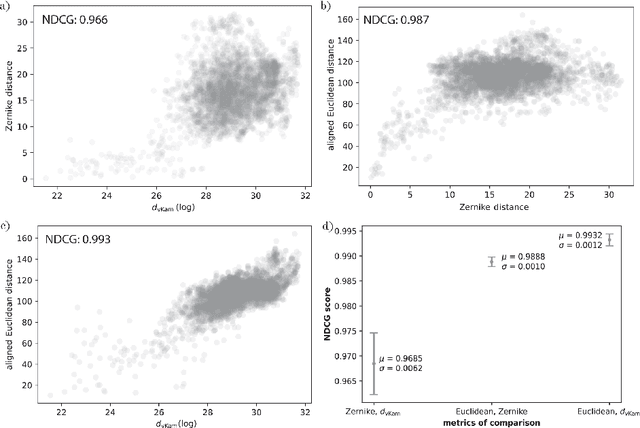
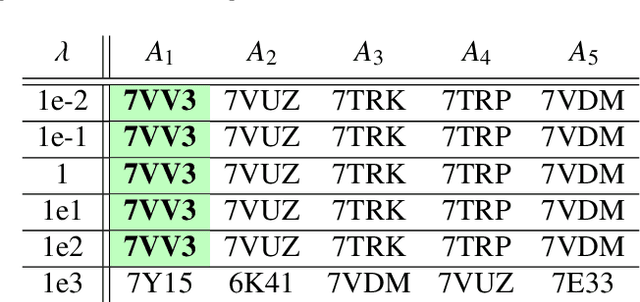
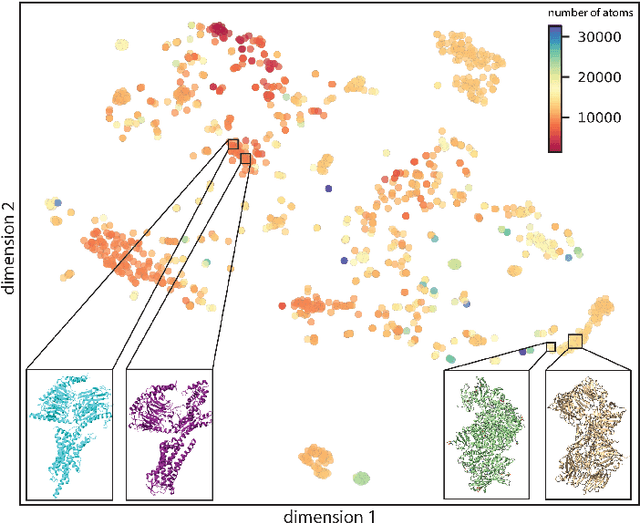
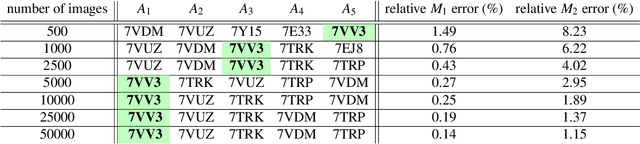
Single particle cryogenic electron microscopy (cryo-EM) is an imaging technique capable of recovering the high-resolution 3-D structure of biological macromolecules from many noisy and randomly oriented projection images. One notable approach to 3-D reconstruction, known as Kam's method, relies on the moments of the 2-D images. Inspired by Kam's method, we introduce a rotationally invariant metric between two molecular structures, which does not require 3-D alignment. Further, we introduce a metric between a stack of projection images and a molecular structure, which is invariant to rotations and reflections and does not require performing 3-D reconstruction. Additionally, the latter metric does not assume a uniform distribution of viewing angles. We demonstrate uses of the new metrics on synthetic and experimental datasets, highlighting their ability to measure structural similarity.

Fast expansion into harmonics on the disk: a steerable basis with fast radial convolutions

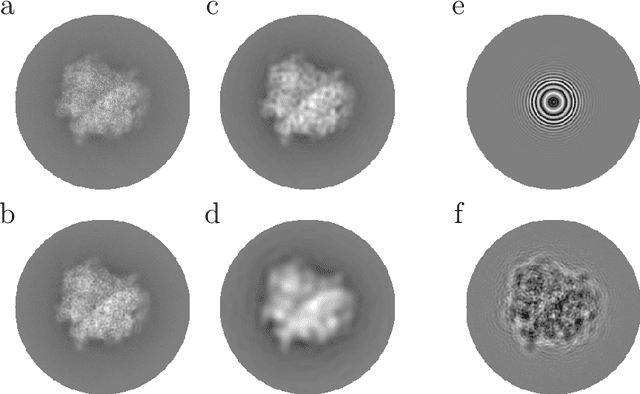
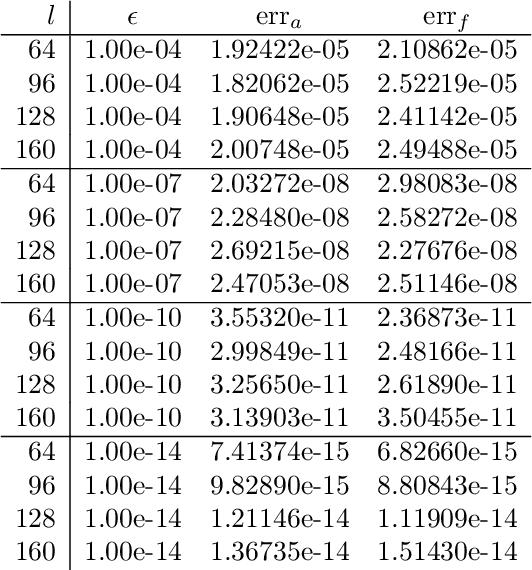
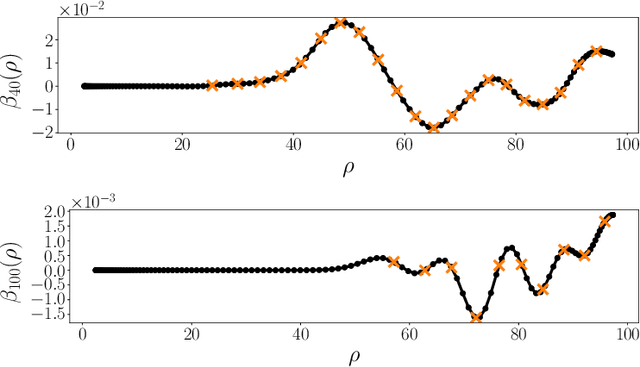
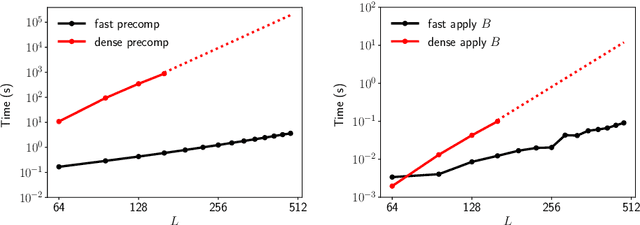
We present a fast and numerically accurate method for expanding digitized $L \times L$ images representing functions on $[-1,1]^2$ supported on the disk $\{x \in \mathbb{R}^2 : |x|<1\}$ in the harmonics (Dirichlet Laplacian eigenfunctions) on the disk. Our method runs in $\mathcal{O}(L^2 \log L)$ operations. This basis is also known as the Fourier-Bessel basis and it has several computational advantages: it is orthogonal, ordered by frequency, and steerable in the sense that images expanded in the basis can be rotated by applying a diagonal transform to the coefficients. Moreover, we show that convolution with radial functions can also be efficiently computed by applying a diagonal transform to the coefficients.

An optimal scheduled learning rate for a randomized Kaczmarz algorithm

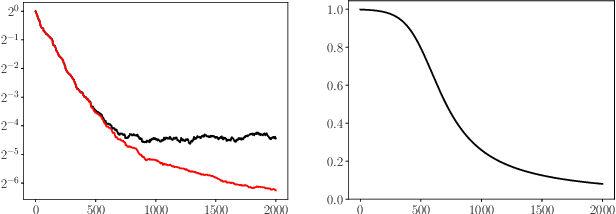
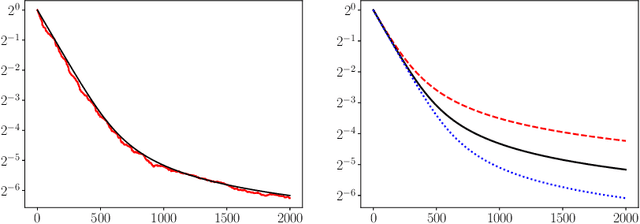
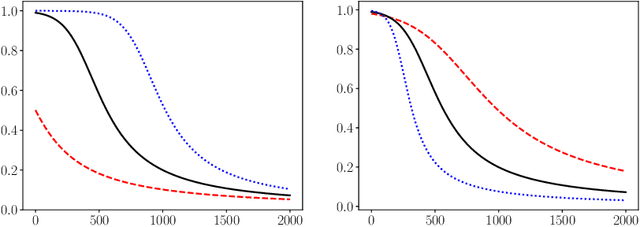
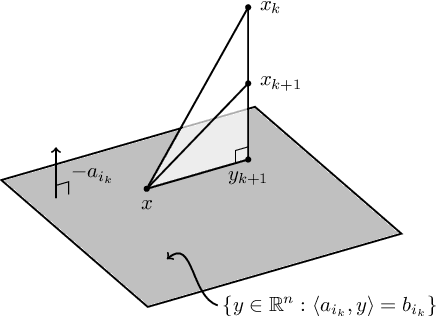
We study how the learning rate affects the performance of a relaxed randomized Kaczmarz algorithm for solving $A x \approx b + \varepsilon$, where $A x =b$ is a consistent linear system and $\varepsilon$ has independent mean zero random entries. We derive a learning rate schedule which optimizes a bound on the expected error that is sharp in certain cases; in contrast to the exponential convergence of the standard randomized Kaczmarz algorithm, our optimized bound involves the reciprocal of the Lambert-$W$ function of an exponential.

Sparse multi-reference alignment: sample complexity and computational hardness

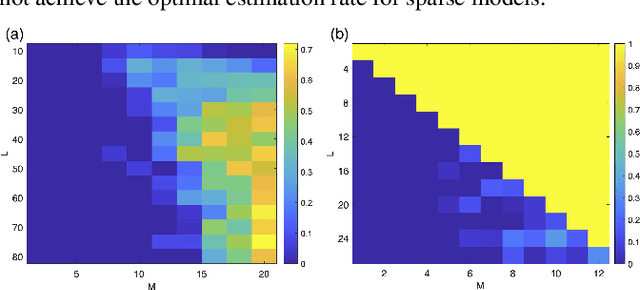
Motivated by the problem of determining the atomic structure of macromolecules using single-particle cryo-electron microscopy (cryo-EM), we study the sample and computational complexities of the sparse multi-reference alignment (MRA) model: the problem of estimating a sparse signal from its noisy, circularly shifted copies. Based on its tight connection to the crystallographic phase retrieval problem, we establish that if the number of observations is proportional to the square of the variance of the noise, then the sparse MRA problem is statistically feasible for sufficiently sparse signals. To investigate its computational hardness, we consider three types of computational frameworks: projection-based algorithms, bispectrum inversion, and convex relaxations. We show that a state-of-the-art projection-based algorithm achieves the optimal estimation rate, but its computational complexity is exponential in the sparsity level. The bispectrum framework provides a statistical-computational trade-off: it requires more observations (so its estimation rate is suboptimal), but its computational load is provably polynomial in the signal's length. The convex relaxation approach provides polynomial time algorithms (with a large exponent) that recover sufficiently sparse signals at the optimal estimation rate. We conclude the paper by discussing potential statistical and algorithmic implications for cryo-EM.