An optimal scheduled learning rate for a randomized Kaczmarz algorithm
Paper and Code
Apr 04, 2022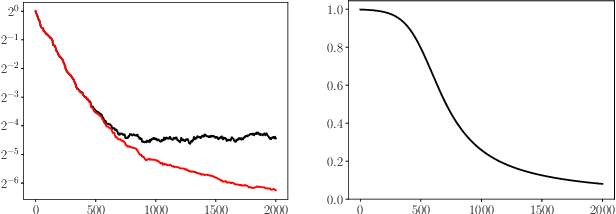
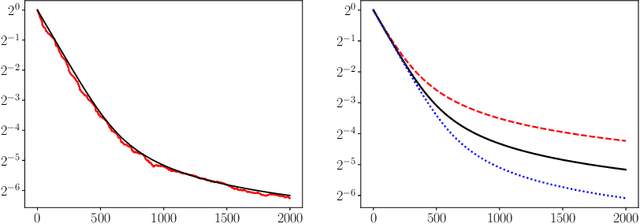
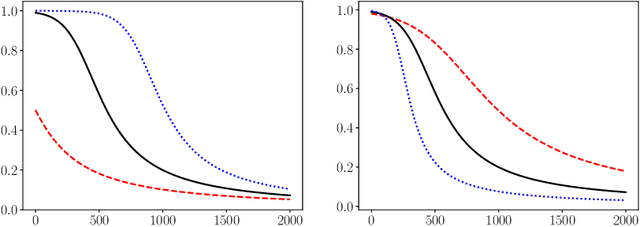
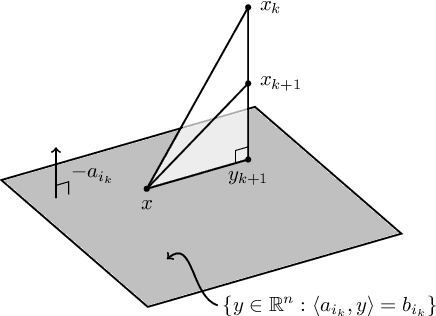
We study how the learning rate affects the performance of a relaxed randomized Kaczmarz algorithm for solving $A x \approx b + \varepsilon$, where $A x =b$ is a consistent linear system and $\varepsilon$ has independent mean zero random entries. We derive a learning rate schedule which optimizes a bound on the expected error that is sharp in certain cases; in contrast to the exponential convergence of the standard randomized Kaczmarz algorithm, our optimized bound involves the reciprocal of the Lambert-$W$ function of an exponential.
* 16 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge