Outlier Removal in Cryo-EM via Radial Profiles

The process of particle picking, a crucial step in cryo-electron microscopy (cryo-EM) image analysis, often encounters challenges due to outliers, leading to inaccuracies in downstream processing. In response to this challenge, this research introduces an additional automated step to reduce the number of outliers identified by the particle picker. The proposed method enhances both the accuracy and efficiency of particle picking, thereby reducing the overall running time and the necessity for expert intervention in the process. Experimental results demonstrate the effectiveness of the proposed approach in mitigating outlier inclusion and its potential to enhance cryo-EM data analysis pipelines significantly. This work contributes to the ongoing advancement of automated cryo-EM image processing methods, offering novel insights and solutions to challenges in structural biology research.

Wavelets Are All You Need for Autoregressive Image Generation

In this paper, we take a new approach to autoregressive image generation that is based on two main ingredients. The first is wavelet image coding, which allows to tokenize the visual details of an image from coarse to fine details by ordering the information starting with the most significant bits of the most significant wavelet coefficients. The second is a variant of a language transformer whose architecture is re-designed and optimized for token sequences in this 'wavelet language'. The transformer learns the significant statistical correlations within a token sequence, which are the manifestations of well-known correlations between the wavelet subbands at various resolutions. We show experimental results with conditioning on the generation process.

Efficient Trajectory Inference in Wasserstein Space Using Consecutive Averaging

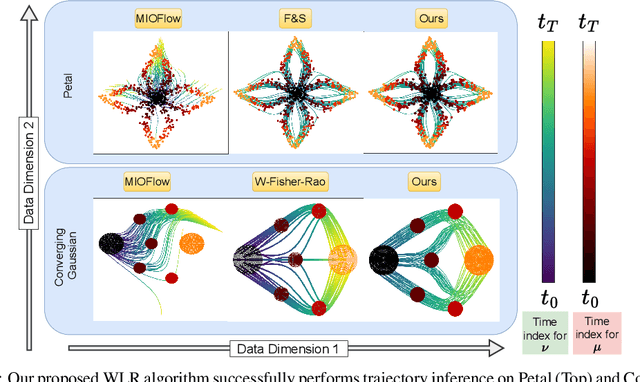
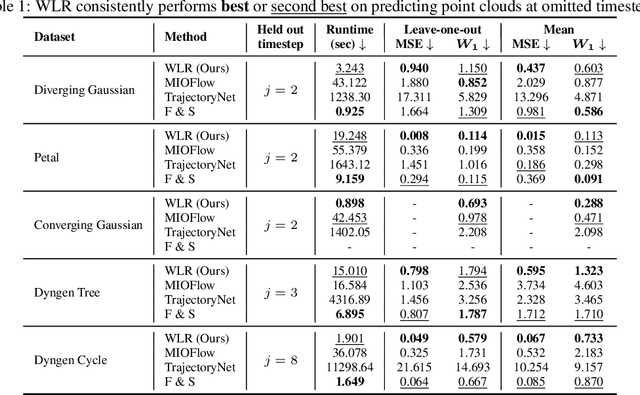
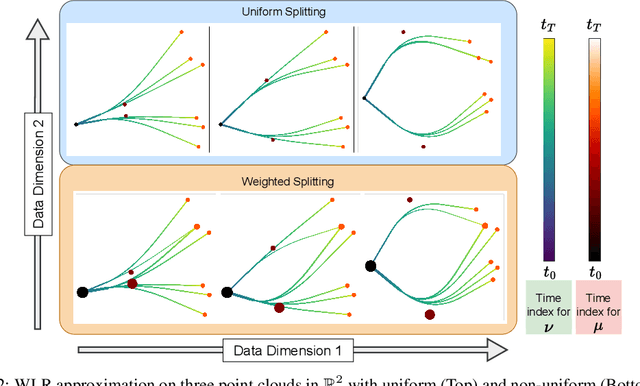
Capturing data from dynamic processes through cross-sectional measurements is seen in many fields such as computational biology. Trajectory inference deals with the challenge of reconstructing continuous processes from such observations. In this work, we propose methods for B-spline approximation and interpolation of point clouds through consecutive averaging that is instrinsic to the Wasserstein space. Combining subdivision schemes with optimal transport-based geodesic, our methods carry out trajectory inference at a chosen level of precision and smoothness, and can automatically handle scenarios where particles undergo division over time. We rigorously evaluate our method by providing convergence guarantees and testing it on simulated cell data characterized by bifurcations and merges, comparing its performance against state-of-the-art trajectory inference and interpolation methods. The results not only underscore the effectiveness of our method in inferring trajectories, but also highlight the benefit of performing interpolation and approximation that respect the inherent geometric properties of the data.

Function Extrapolation with Neural Networks and Its Application for Manifolds

This paper addresses the problem of accurately estimating a function on one domain when only its discrete samples are available on another domain. To answer this challenge, we utilize a neural network, which we train to incorporate prior knowledge of the function. In addition, by carefully analyzing the problem, we obtain a bound on the error over the extrapolation domain and define a condition number for this problem that quantifies the level of difficulty of the setup. Compared to other machine learning methods that provide time series prediction, such as transformers, our approach is suitable for setups where the interpolation and extrapolation regions are general subdomains and, in particular, manifolds. In addition, our construction leads to an improved loss function that helps us boost the accuracy and robustness of our neural network. We conduct comprehensive numerical tests and comparisons of our extrapolation versus standard methods. The results illustrate the effectiveness of our approach in various scenarios.

Deep Neural-network Prior for Orbit Recovery from Method of Moments

Orbit recovery problems are a class of problems that often arise in practice and in various forms. In these problems, we aim to estimate an unknown function after being distorted by a group action and observed via a known operator. Typically, the observations are contaminated with a non-trivial level of noise. Two particular orbit recovery problems of interest in this paper are multireference alignment and single-particle cryo-EM modeling. In order to suppress the noise, we suggest using the method of moments approach for both problems while introducing deep neural network priors. In particular, our neural networks should output the signals and the distribution of group elements, with moments being the input. In the multireference alignment case, we demonstrate the advantage of using the NN to accelerate the convergence for the reconstruction of signals from the moments. Finally, we use our method to reconstruct simulated and biological volumes in the cryo-EM setting.

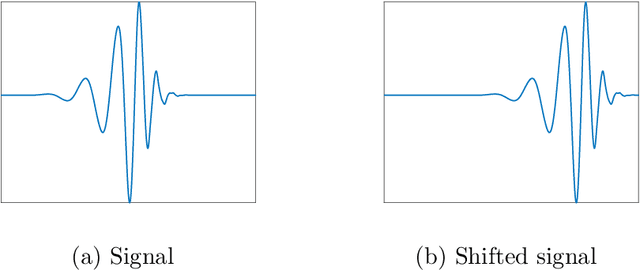
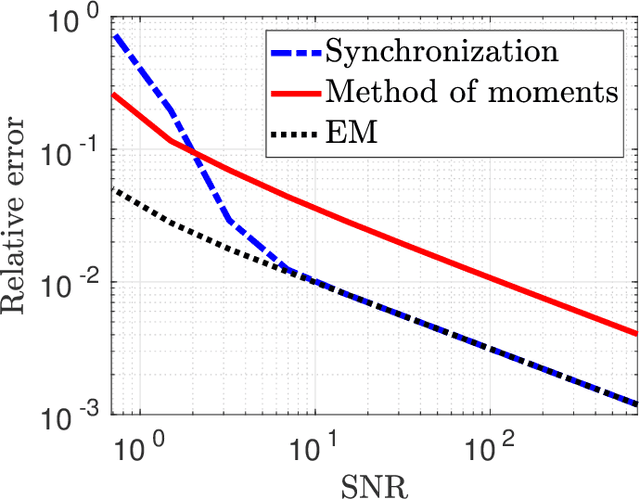
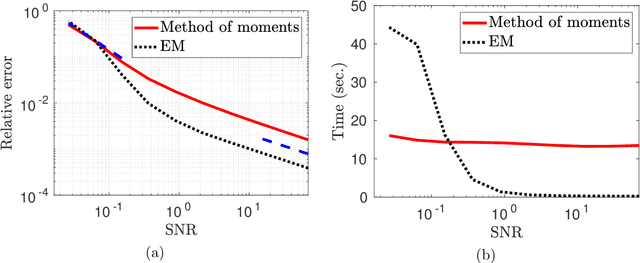
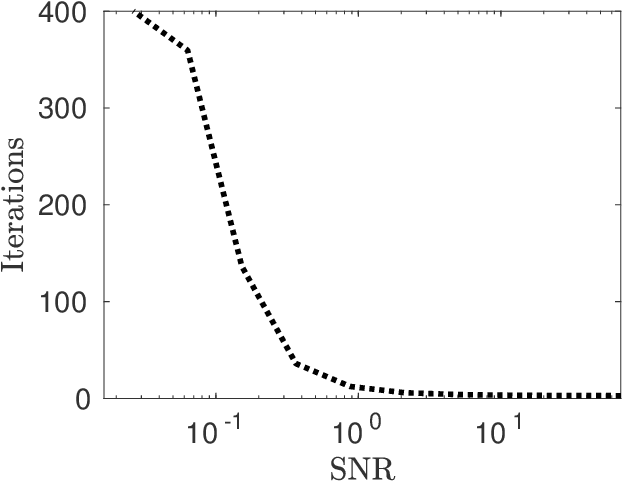
Dihedral multi-reference alignment

We study the dihedral multi-reference alignment problem of estimating the orbit of a signal from multiple noisy observations of the signal, translated by random elements of the dihedral group. We show that if the group elements are drawn from a generic distribution, the orbit of a generic signal is uniquely determined from the second moment of the observations. This implies that the optimal estimation rate in the high noise regime is proportional to the square of the variance of the noise. This is the first result of this type for multi-reference alignment over a non-abelian group with a non-uniform distribution of group elements. Based on tools from invariant theory and algebraic geometry, we also delineate conditions for unique orbit recovery for multi-reference alignment models over finite groups (namely, when the dihedral group is replaced by a general finite group) when the group elements are drawn from a generic distribution. Finally, we design and study numerically three computational frameworks for estimating the signal based on group synchronization, expectation-maximization, and the method of moments.

Compactification of the Rigid Motions Group in Image Processing

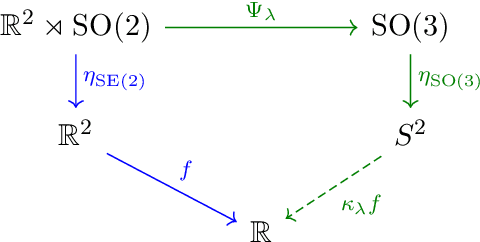
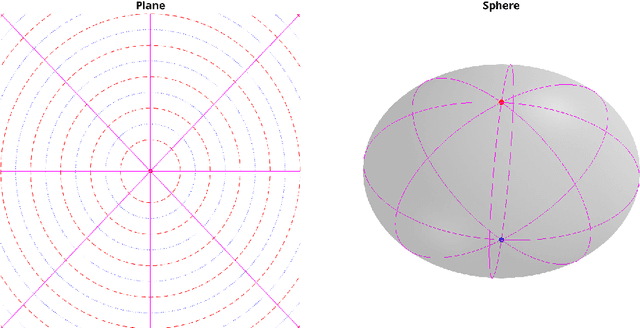
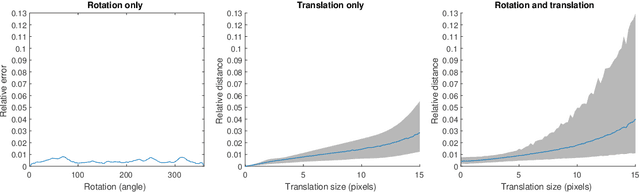
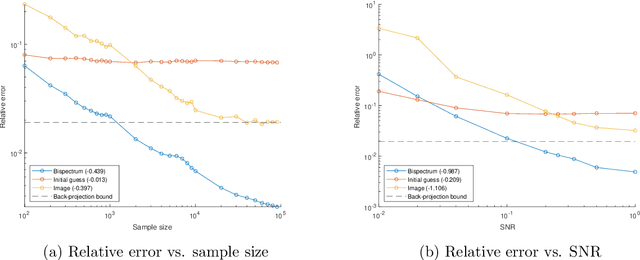
Image processing problems in general, and in particular in the field of single-particle cryo-electron microscopy, often require considering images up to their rotations and translations. Such problems were tackled successfully when considering images up to rotations only, using quantities which are invariant to the action of rotations on images. Extending these methods to cases where translations are involved is more complicated. Here we present a computationally feasible and theoretically sound approximate invariant to the action of rotations and translations on images. It allows one to approximately reduce image processing problems to similar problems over the sphere, a compact domain acted on by the group of 3D rotations, a compact group. We show that this invariant is induced by a family of mappings deforming, and thereby compactifying, the group structure of rotations and translations of the plane, i.e., the group of rigid motions, into the group of 3D rotations. Furthermore, we demonstrate its viability in two image processing tasks: multi-reference alignment and classification. To our knowledge, this is the first instance of a quantity that is either exactly or approximately invariant to rotations and translations of images that both rests on a sound theoretical foundation and also applicable in practice.

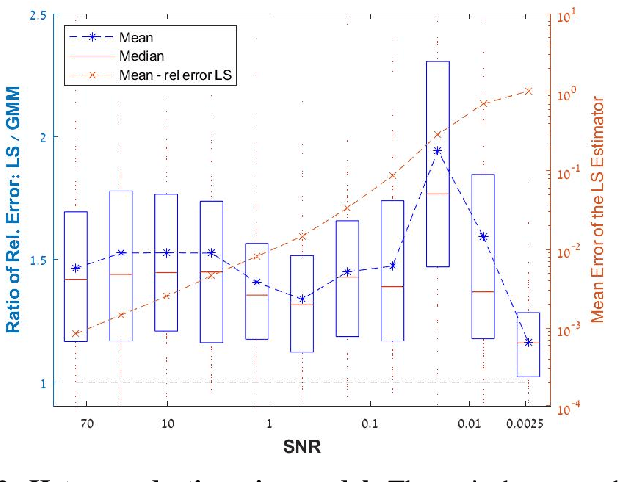
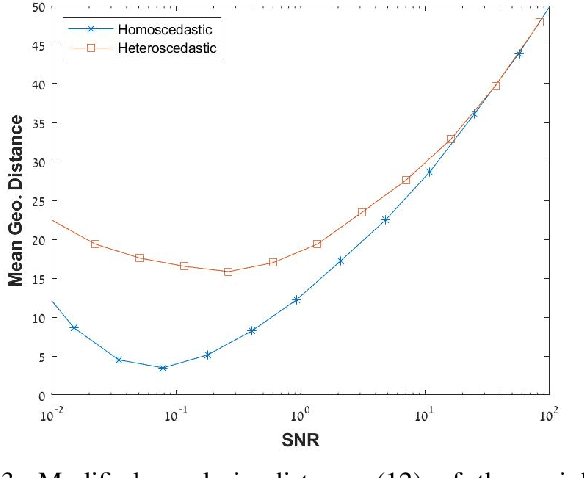
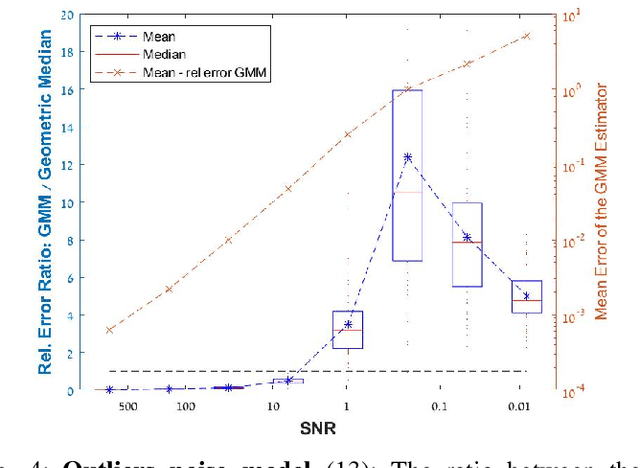
The generalized method of moments for multi-reference alignment

This paper studies the application of the generalized method of moments (GMM) to multi-reference alignment (MRA): the problem of estimating a signal from its circularly-translated and noisy copies. We begin by proving that the GMM estimator maintains its asymptotic optimality for statistical models with group symmetry, including MRA. Then, we conduct a comprehensive numerical study and show that the GMM substantially outperforms the classical method of moments, whose application to MRA has been studied thoroughly in the literature. We also formulate the GMM to estimate a three-dimensional molecular structure using cryo-electron microscopy and present numerical results on simulated data.

An algorithm for improving Non-Local Means operators via low-rank approximation

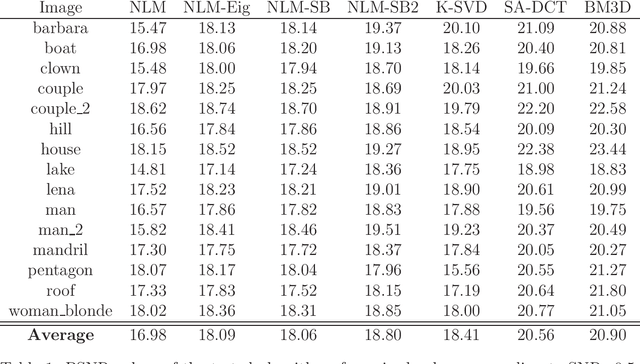
We present a method for improving a Non Local Means operator by computing its low-rank approximation. The low-rank operator is constructed by applying a filter to the spectrum of the original Non Local Means operator. This results in an operator which is less sensitive to noise while preserving important properties of the original operator. The method is efficiently implemented based on Chebyshev polynomials and is demonstrated on the application of natural images denoising. For this application, we provide a comprehensive comparison of our method with leading denoising methods.