Matrix Denoising with Partial Noise Statistics: Optimal Singular Value Shrinkage of Spiked F-Matrices

We study the problem of estimating a large, low-rank matrix corrupted by additive noise of unknown covariance, assuming one has access to additional side information in the form of noise-only measurements. We study the Whiten-Shrink-reColor (WSC) workflow, where a "noise covariance whitening" transformation is applied to the observations, followed by appropriate singular value shrinkage and a "noise covariance re-coloring" transformation. We show that under the mean square error loss, a unique, asymptotically optimal shrinkage nonlinearity exists for the WSC denoising workflow, and calculate it in closed form. To this end, we calculate the asymptotic eigenvector rotation of the random spiked F-matrix ensemble, a result which may be of independent interest. With sufficiently many pure-noise measurements, our optimally-tuned WSC denoising workflow outperforms, in mean square error, matrix denoising algorithms based on optimal singular value shrinkage which do not make similar use of noise-only side information; numerical experiments show that our procedure's relative performance is particularly strong in challenging statistical settings with high dimensionality and large degree of heteroscedasticity.

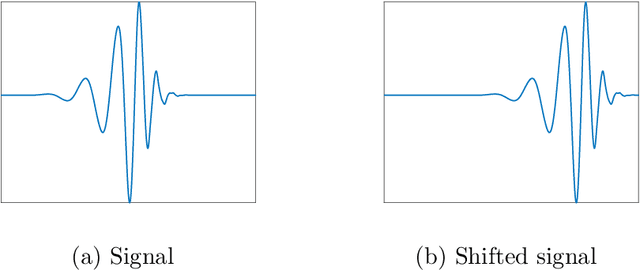
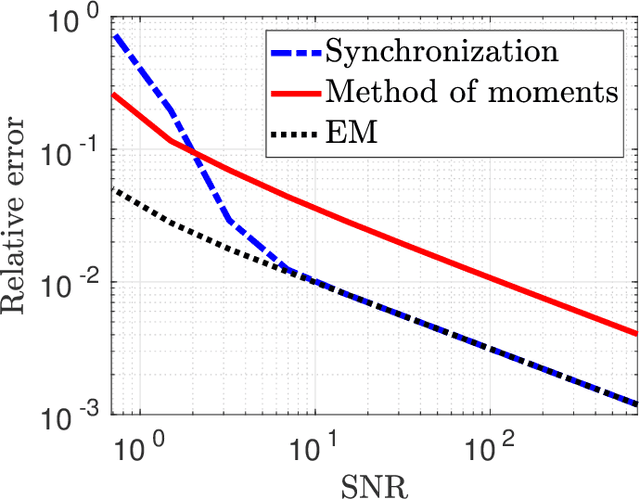
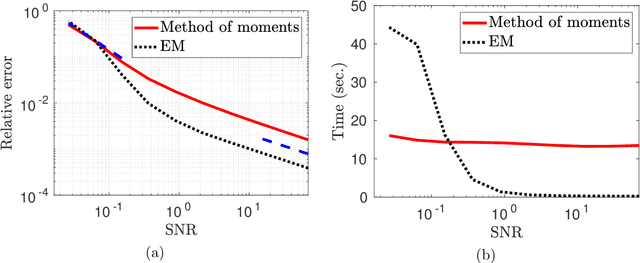
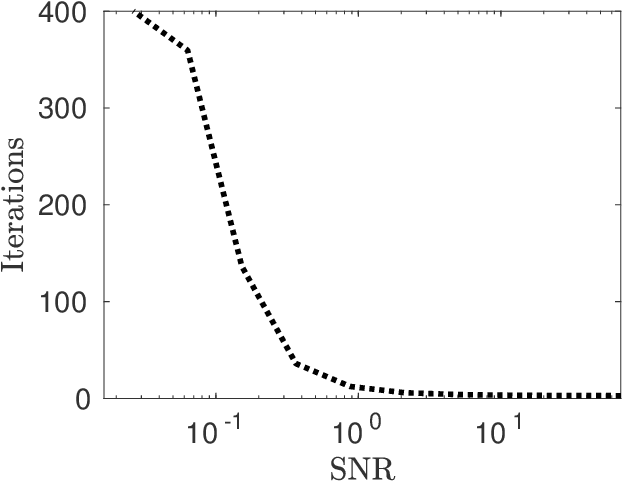
Dihedral multi-reference alignment

We study the dihedral multi-reference alignment problem of estimating the orbit of a signal from multiple noisy observations of the signal, translated by random elements of the dihedral group. We show that if the group elements are drawn from a generic distribution, the orbit of a generic signal is uniquely determined from the second moment of the observations. This implies that the optimal estimation rate in the high noise regime is proportional to the square of the variance of the noise. This is the first result of this type for multi-reference alignment over a non-abelian group with a non-uniform distribution of group elements. Based on tools from invariant theory and algebraic geometry, we also delineate conditions for unique orbit recovery for multi-reference alignment models over finite groups (namely, when the dihedral group is replaced by a general finite group) when the group elements are drawn from a generic distribution. Finally, we design and study numerically three computational frameworks for estimating the signal based on group synchronization, expectation-maximization, and the method of moments.

Properties of Laplacian Pyramids for Extension and Denoising

We analyze the Laplacian pyramids algorithm of Rabin and Coifman for extending and denoising a function sampled on a discrete set of points. We provide mild conditions under which the algorithm converges, and prove stability bounds on the extended function. We also consider the iterative application of truncated Laplacian pyramids kernels for denoising signals by non-local means.

Matrix denoising for weighted loss functions and heterogeneous signals

We consider the problem of recovering a low-rank matrix from a noisy observed matrix. Previous work has shown that the optimal method for recovery depends crucially on the choice of loss function. We use a family of weighted loss functions, which arise naturally in many settings such as heteroscedastic noise and missing data. Weighted loss functions are challenging to analyze because they are not orthogonally-invariant. We derive optimal spectral denoisers for these weighted loss functions. By combining different weights, we then use these optimal denoisers to construct a new denoiser that exploits heterogeneity in the signal matrix for more accurate recovery with unweighted loss.