Ranking of Multi-Response Experiment Treatments

We present a probabilistic ranking model to identify the optimal treatment in multiple-response experiments. In contemporary practice, treatments are applied over individuals with the goal of achieving multiple ideal properties on them simultaneously. However, often there are competing properties, and the optimality of one cannot be achieved without compromising the optimality of another. Typically, we still want to know which treatment is the overall best. In our framework, we first formulate overall optimality in terms of treatment ranks. Then we infer the latent ranking that allow us to report treatments from optimal to least optimal, provided ideal desirable properties. We demonstrate through simulations and real data analysis how we can achieve reliability of inferred ranks in practice. We adopt a Bayesian approach and derive an associated Markov Chain Monte Carlo algorithm to fit our model to data. Finally, we discuss the prospects of adoption of our method as a standard tool for experiment evaluation in trials-based research.

Matrix Denoising with Partial Noise Statistics: Optimal Singular Value Shrinkage of Spiked F-Matrices

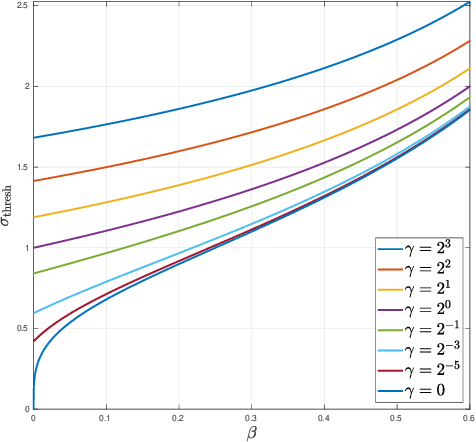
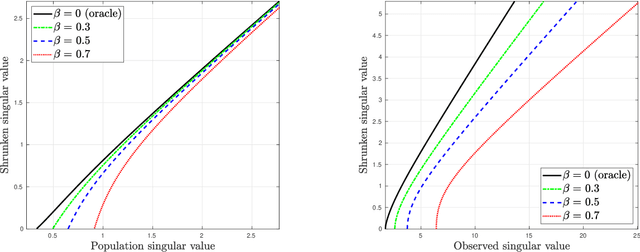
We study the problem of estimating a large, low-rank matrix corrupted by additive noise of unknown covariance, assuming one has access to additional side information in the form of noise-only measurements. We study the Whiten-Shrink-reColor (WSC) workflow, where a "noise covariance whitening" transformation is applied to the observations, followed by appropriate singular value shrinkage and a "noise covariance re-coloring" transformation. We show that under the mean square error loss, a unique, asymptotically optimal shrinkage nonlinearity exists for the WSC denoising workflow, and calculate it in closed form. To this end, we calculate the asymptotic eigenvector rotation of the random spiked F-matrix ensemble, a result which may be of independent interest. With sufficiently many pure-noise measurements, our optimally-tuned WSC denoising workflow outperforms, in mean square error, matrix denoising algorithms based on optimal singular value shrinkage which do not make similar use of noise-only side information; numerical experiments show that our procedure's relative performance is particularly strong in challenging statistical settings with high dimensionality and large degree of heteroscedasticity.

LOCA: LOcal Conformal Autoencoder for standardized data coordinates

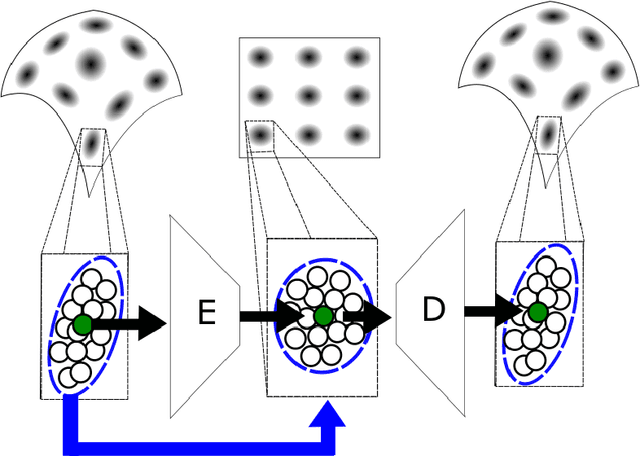
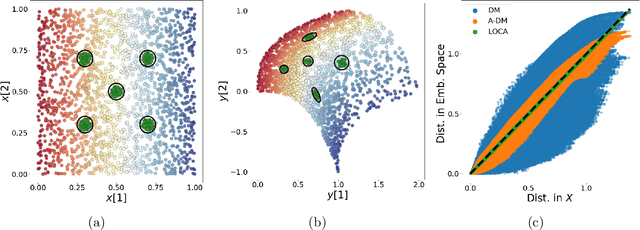
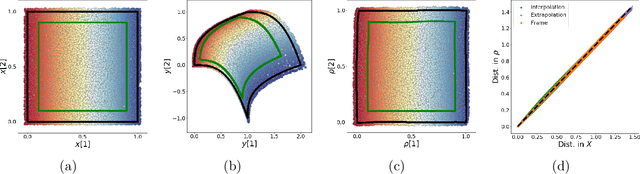
We propose a deep-learning based method for obtaining standardized data coordinates from scientific measurements.Data observations are modeled as samples from an unknown, non-linear deformation of an underlying Riemannian manifold, which is parametrized by a few normalized latent variables. By leveraging a repeated measurement sampling strategy, we present a method for learning an embedding in $\mathbb{R}^d$ that is isometric to the latent variables of the manifold. These data coordinates, being invariant under smooth changes of variables, enable matching between different instrumental observations of the same phenomenon. Our embedding is obtained using a LOcal Conformal Autoencoder (LOCA), an algorithm that constructs an embedding to rectify deformations by using a local z-scoring procedure while preserving relevant geometric information. We demonstrate the isometric embedding properties of LOCA on various model settings and observe that it exhibits promising interpolation and extrapolation capabilities. Finally, we apply LOCA to single-site Wi-Fi localization data, and to $3$-dimensional curved surface estimation based on a $2$-dimensional projection.

Optimal Shrinkage of Singular Values Under Random Data Contamination

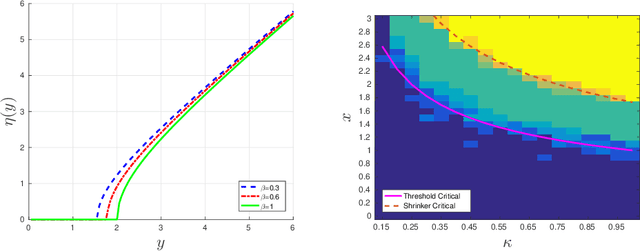
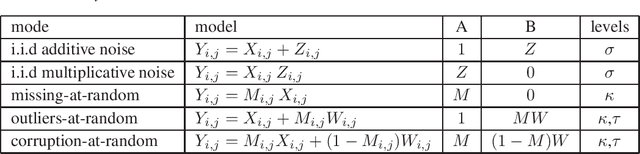
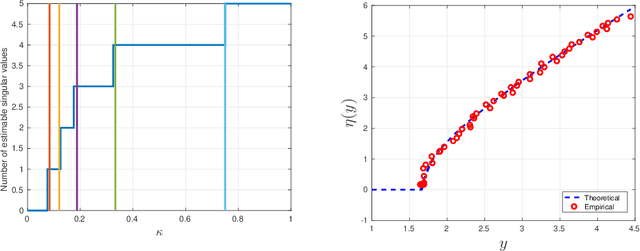
A low rank matrix X has been contaminated by uniformly distributed noise, missing values, outliers and corrupt entries. Reconstruction of X from the singular values and singular vectors of the contaminated matrix Y is a key problem in machine learning, computer vision and data science. In this paper we show that common contamination models (including arbitrary combinations of uniform noise,missing values, outliers and corrupt entries) can be described efficiently using a single framework. We develop an asymptotically optimal algorithm that estimates X by manipulation of the singular values of Y , which applies to any of the contamination models considered. Finally, we find an explicit signal-to-noise cutoff, below which estimation of X from the singular value decomposition of Y must fail, in a well-defined sense.

ReFACTor: Practical Low-Rank Matrix Estimation Under Column-Sparsity

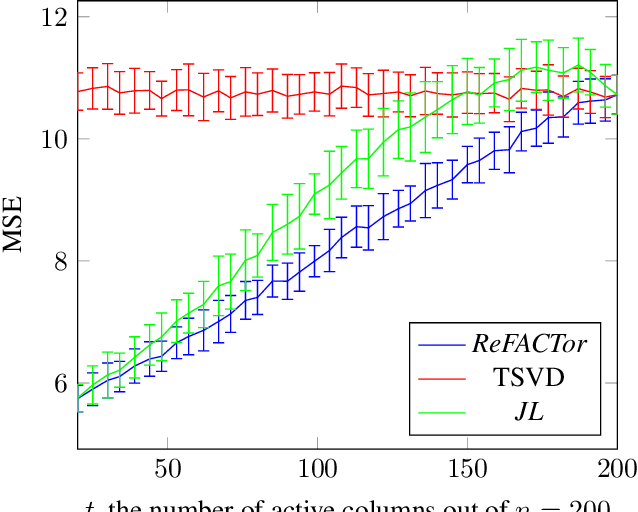
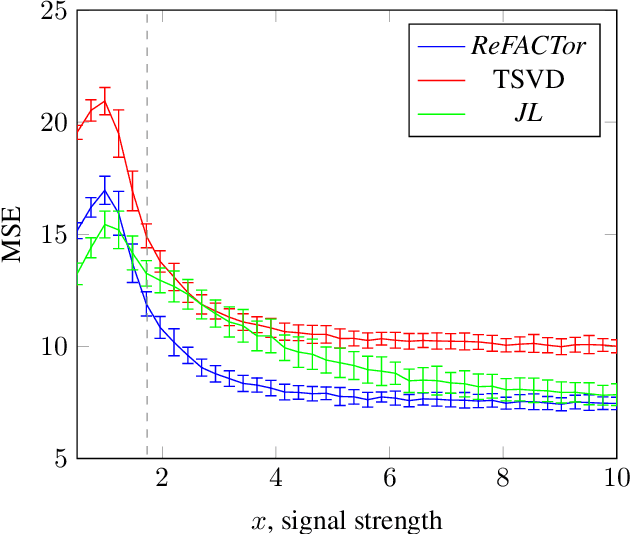
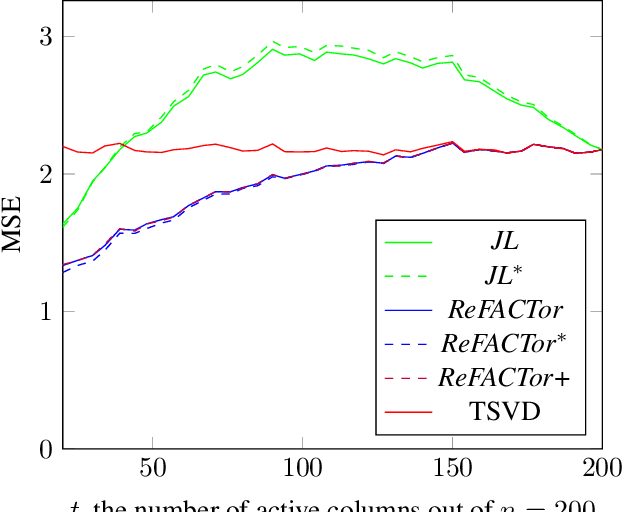
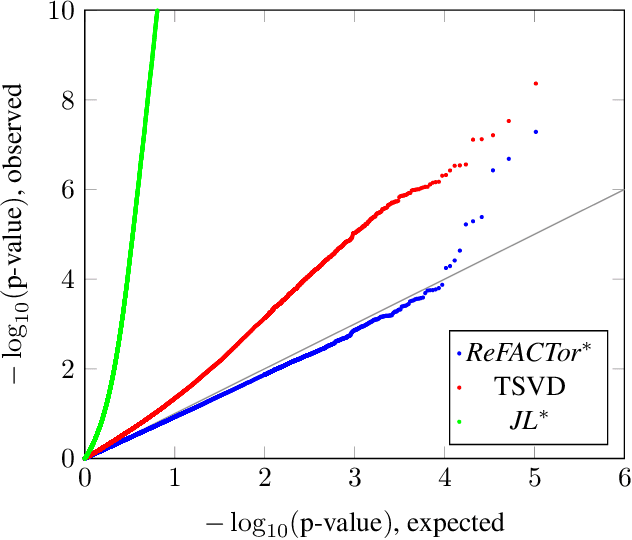
Various problems in data analysis and statistical genetics call for recovery of a column-sparse, low-rank matrix from noisy observations. We propose ReFACTor, a simple variation of the classical Truncated Singular Value Decomposition (TSVD) algorithm. In contrast to previous sparse principal component analysis (PCA) algorithms, our algorithm can provably reveal a low-rank signal matrix better, and often significantly better, than the widely used TSVD, making it the algorithm of choice whenever column-sparsity is suspected. Empirically, we observe that ReFACTor consistently outperforms TSVD even when the underlying signal is not sparse, suggesting that it is generally safe to use ReFACTor instead of TSVD and PCA. The algorithm is extremely simple to implement and its running time is dominated by the runtime of PCA, making it as practical as standard principal component analysis.

The Maximum Entropy Relaxation Path

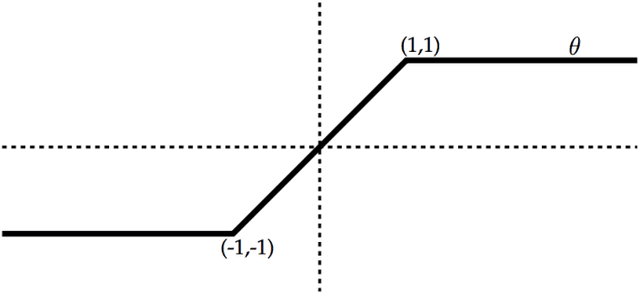
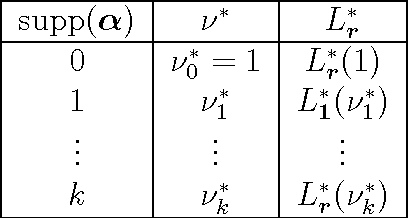
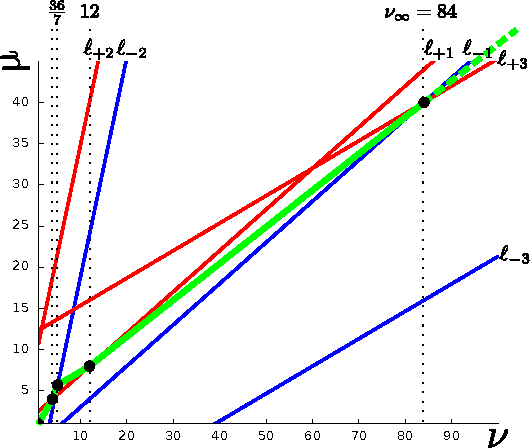
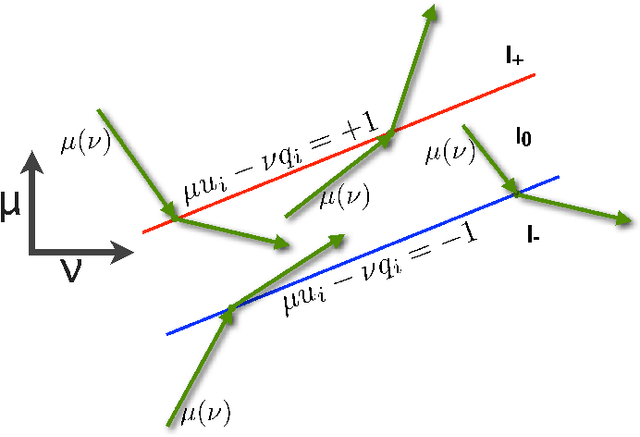
The relaxed maximum entropy problem is concerned with finding a probability distribution on a finite set that minimizes the relative entropy to a given prior distribution, while satisfying relaxed max-norm constraints with respect to a third observed multinomial distribution. We study the entire relaxation path for this problem in detail. We show existence and a geometric description of the relaxation path. Specifically, we show that the maximum entropy relaxation path admits a planar geometric description as an increasing, piecewise linear function in the inverse relaxation parameter. We derive fast algorithms for tracking the path. In various realistic settings, our algorithms require $O(n\log(n))$ operations for probability distributions on $n$ points, making it possible to handle large problems. Once the path has been recovered, we show that given a validation set, the family of admissible models is reduced from an infinite family to a small, discrete set. We demonstrate the merits of our approach in experiments with synthetic data and discuss its potential for the estimation of compact n-gram language models.