The Maximum Entropy Relaxation Path
Paper and Code
Nov 07, 2013
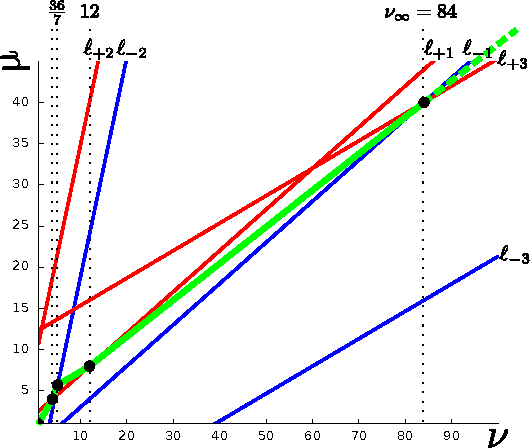
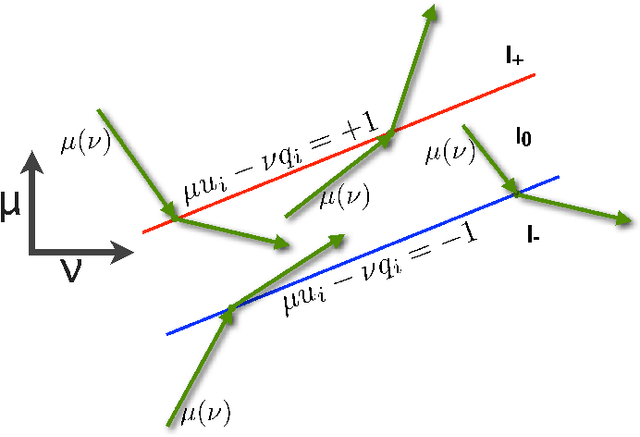
The relaxed maximum entropy problem is concerned with finding a probability distribution on a finite set that minimizes the relative entropy to a given prior distribution, while satisfying relaxed max-norm constraints with respect to a third observed multinomial distribution. We study the entire relaxation path for this problem in detail. We show existence and a geometric description of the relaxation path. Specifically, we show that the maximum entropy relaxation path admits a planar geometric description as an increasing, piecewise linear function in the inverse relaxation parameter. We derive fast algorithms for tracking the path. In various realistic settings, our algorithms require $O(n\log(n))$ operations for probability distributions on $n$ points, making it possible to handle large problems. Once the path has been recovered, we show that given a validation set, the family of admissible models is reduced from an infinite family to a small, discrete set. We demonstrate the merits of our approach in experiments with synthetic data and discuss its potential for the estimation of compact n-gram language models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge