Yoram Singer
AT&T Research
Second Order Optimization Made Practical
Feb 20, 2020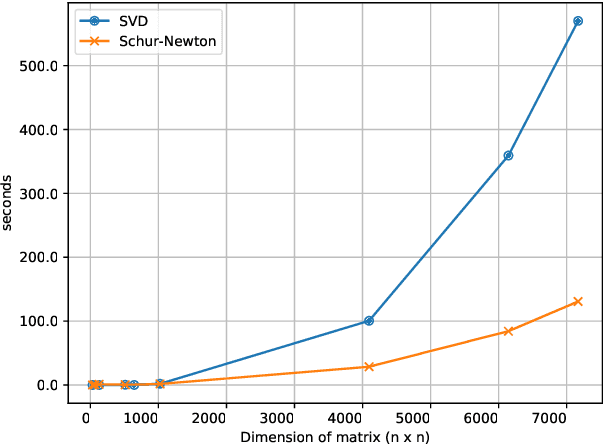

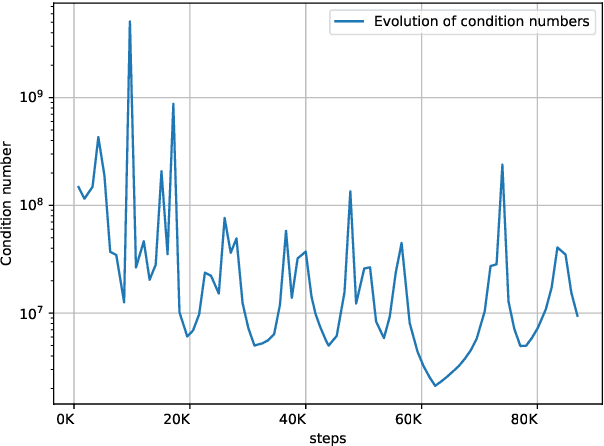

Abstract:Optimization in machine learning, both theoretical and applied, is presently dominated by first-order gradient methods such as stochastic gradient descent. Second-order optimization methods that involve second-order derivatives and/or second-order statistics of the data have become far less prevalent despite strong theoretical properties, due to their prohibitive computation, memory and communication costs. In an attempt to bridge this gap between theoretical and practical optimization, we present a proof-of-concept distributed system implementation of a second-order preconditioned method (specifically, a variant of full-matrix Adagrad), that along with a few yet critical algorithmic and numerical improvements, provides significant practical gains in convergence on state-of-the-art deep models and gives rise to actual wall-time improvements in practice compared to conventional first-order methods. Our design effectively utilizes the prevalent heterogeneous hardware architecture for training deep models which consists of a multicore CPU coupled with multiple accelerator units. We demonstrate superior performance on very large learning problems in machine translation where our distributed implementation runs considerably faster than existing gradient-based methods.
Proximity Preserving Binary Code using Signed Graph-Cut
Feb 05, 2020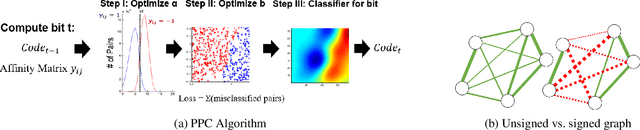
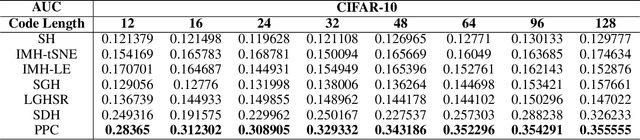

Abstract:We introduce a binary embedding framework, called Proximity Preserving Code (PPC), which learns similarity and dissimilarity between data points to create a compact and affinity-preserving binary code. This code can be used to apply fast and memory-efficient approximation to nearest-neighbor searches. Our framework is flexible, enabling different proximity definitions between data points. In contrast to previous methods that extract binary codes based on unsigned graph partitioning, our system models the attractive and repulsive forces in the data by incorporating positive and negative graph weights. The proposed framework is shown to boil down to finding the minimal cut of a signed graph, a problem known to be NP-hard. We offer an efficient approximation and achieve superior results by constructing the code bit after bit. We show that the proposed approximation is superior to the commonly used spectral methods with respect to both accuracy and complexity. Thus, it is useful for many other problems that can be translated into signed graph cut.
Convolutional Bipartite Attractor Networks
Jun 15, 2019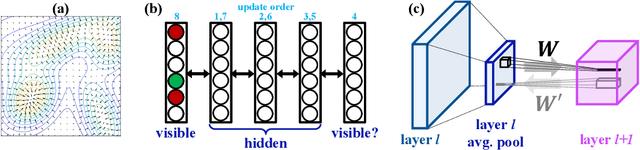


Abstract:In human perception and cognition, the fundamental operation that brains perform is interpretation: constructing coherent neural states from noisy, incomplete, and intrinsically ambiguous evidence. The problem of interpretation is well matched to an early and often overlooked architecture, the attractor network---a recurrent neural network that performs constraint satisfaction, imputation of missing features, and clean up of noisy data via energy minimization dynamics. We revisit attractor nets in light of modern deep learning methods, and propose a convolutional bipartite architecture with a novel training loss, activation function, and connectivity constraints. We tackle problems much larger than have been previously explored with attractor nets and demonstrate their potential for image denoising, completion, and super-resolution. We argue that this architecture is better motivated than ever-deeper feedforward models and is a viable alternative to more costly sampling-based methods on a range of supervised and unsupervised tasks.
Identity Crisis: Memorization and Generalization under Extreme Overparameterization
Feb 15, 2019


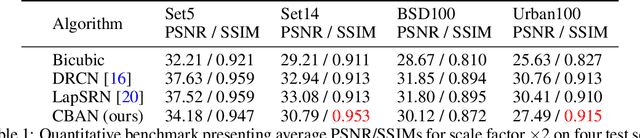
Abstract:We study the interplay between memorization and generalization of overparametrized networks in the extreme case of a single training example. The learning task is to predict an output which is as similar as possible to the input. We examine both fully-connected and convolutional networks that are initialized randomly and then trained to minimize the reconstruction error. The trained networks take one of the two forms: the constant function ("memorization") and the identity function ("generalization"). We show that different architectures exhibit vastly different inductive bias towards memorization and generalization. An important consequence of our study is that even in extreme cases of overparameterization, deep learning can result in proper generalization.
Are All Layers Created Equal?
Feb 12, 2019
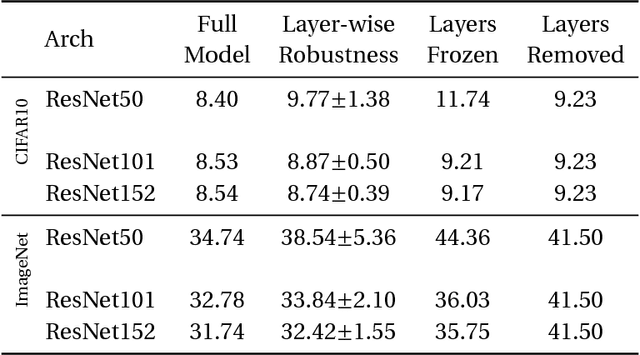
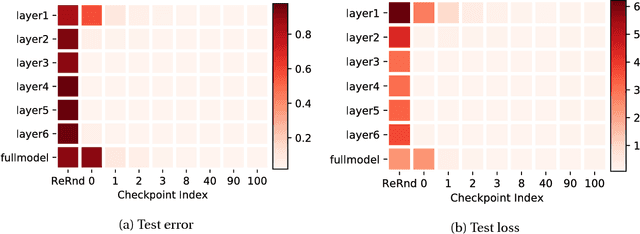
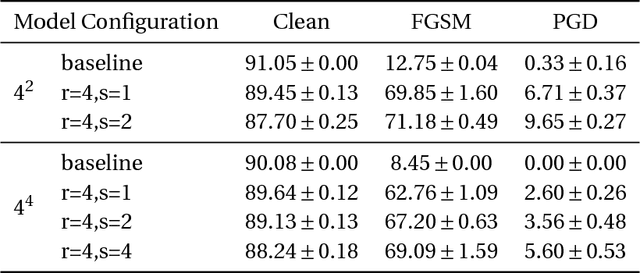
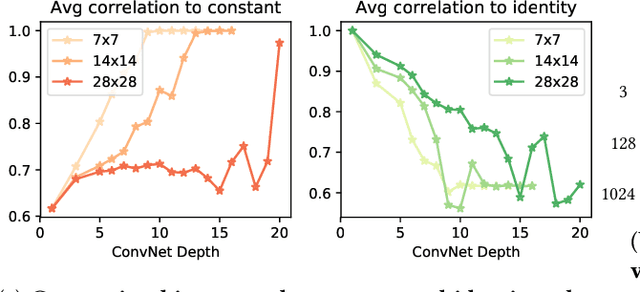
Abstract:Understanding learning and generalization of deep architectures has been a major research objective in the recent years with notable theoretical progress. A main focal point of generalization studies stems from the success of excessively large networks which defy the classical wisdom of uniform convergence and learnability. We study empirically the layer-wise functional structure of overparameterized deep models. We provide evidence for the heterogeneous characteristic of layers. To do so, we introduce the notion of (post training) re-initialization and re-randomization robustness. We show that layers can be categorized into either `robust' or `critical'. In contrast to critical layers, resetting the robust layers to their initial value has no negative consequence, and in many cases they barely change throughout training. Our study provides further evidence that mere parameter counting or norm accounting is too coarse in studying generalization of deep models, and flatness or robustness analysis of the model parameters needs to respect the network architectures.
Exponentiated Gradient Meets Gradient Descent
Feb 05, 2019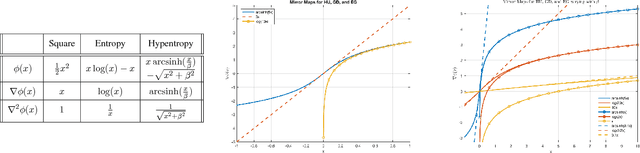
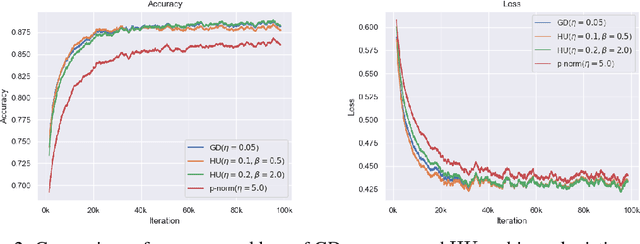
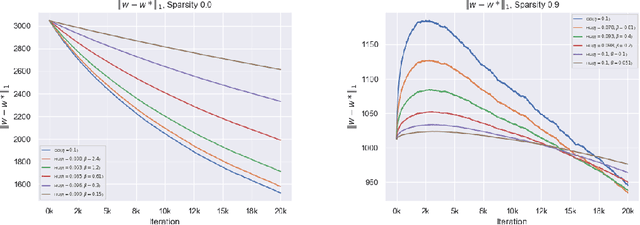
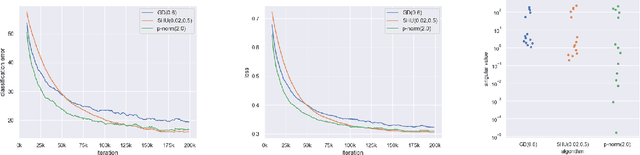
Abstract:The (stochastic) gradient descent and the multiplicative update method are probably the most popular algorithms in machine learning. We introduce and study a new regularization which provides a unification of the additive and multiplicative updates. This regularization is derived from an hyperbolic analogue of the entropy function, which we call hypentropy. It is motivated by a natural extension of the multiplicative update to negative numbers. The hypentropy has a natural spectral counterpart which we use to derive a family of matrix-based updates that bridge gradient methods and the multiplicative method for matrices. While the latter is only applicable to positive semi-definite matrices, the spectral hypentropy method can naturally be used with general rectangular matrices. We analyze the new family of updates by deriving tight regret bounds. We study empirically the applicability of the new update for settings such as multiclass learning, in which the parameters constitute a general rectangular matrix.
Memory-Efficient Adaptive Optimization for Large-Scale Learning
Jan 30, 2019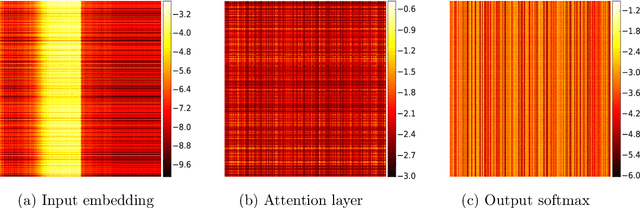
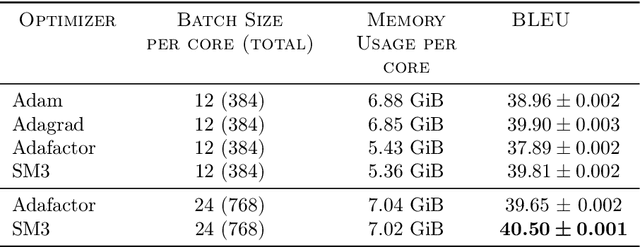
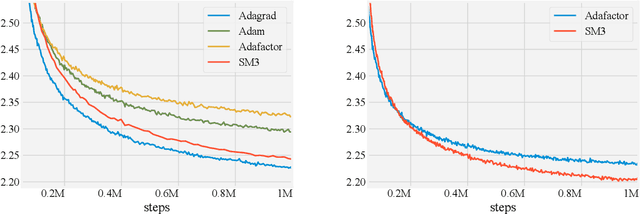
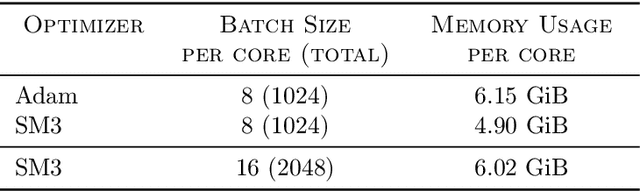
Abstract:Adaptive gradient-based optimizers such as AdaGrad and Adam are among the methods of choice in modern machine learning. These methods maintain second-order statistics of each parameter, thus doubling the memory footprint of the optimizer. In behemoth-size applications, this memory overhead restricts the size of the model being used as well as the number of examples in a mini-batch. We describe a novel, simple, and flexible adaptive optimization method with sublinear memory cost that retains the benefits of per-parameter adaptivity while allowing for larger models and mini-batches. We give convergence guarantees for our method and demonstrate its effectiveness in training very large deep models.
The Well Tempered Lasso
Jun 08, 2018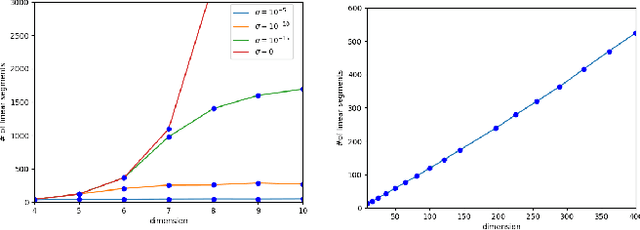
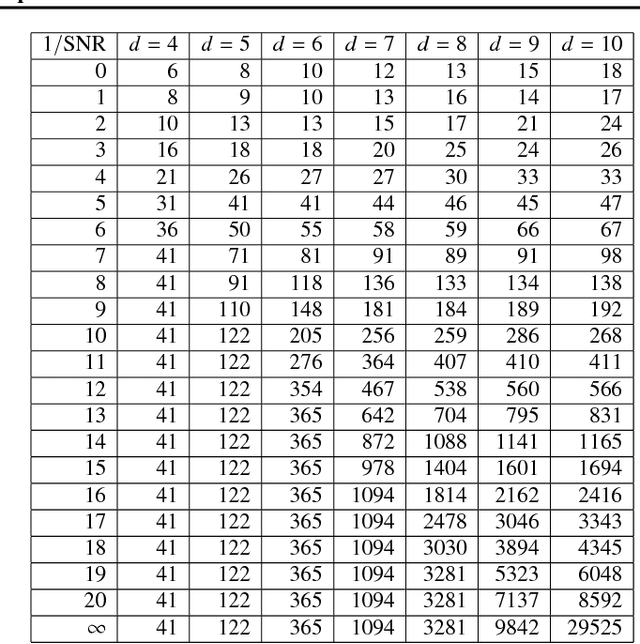
Abstract:We study the complexity of the entire regularization path for least squares regression with 1-norm penalty, known as the Lasso. Every regression parameter in the Lasso changes linearly as a function of the regularization value. The number of changes is regarded as the Lasso's complexity. Experimental results using exact path following exhibit polynomial complexity of the Lasso in the problem size. Alas, the path complexity of the Lasso on artificially designed regression problems is exponential. We use smoothed analysis as a mechanism for bridging the gap between worst case settings and the de facto low complexity. Our analysis assumes that the observed data has a tiny amount of intrinsic noise. We then prove that the Lasso's complexity is polynomial in the problem size. While building upon the seminal work of Spielman and Teng on smoothed complexity, our analysis is morally different as it is divorced from specific path following algorithms. We verify the validity of our analysis in experiments with both worst case settings and real datasets. The empirical results we obtain closely match our analysis.
Shampoo: Preconditioned Stochastic Tensor Optimization
Mar 02, 2018
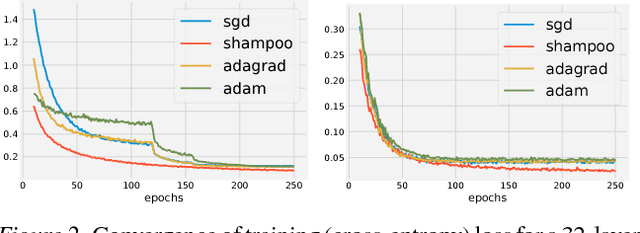
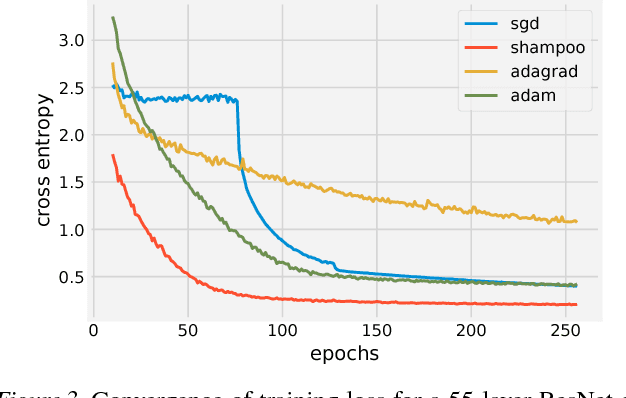
Abstract:Preconditioned gradient methods are among the most general and powerful tools in optimization. However, preconditioning requires storing and manipulating prohibitively large matrices. We describe and analyze a new structure-aware preconditioning algorithm, called Shampoo, for stochastic optimization over tensor spaces. Shampoo maintains a set of preconditioning matrices, each of which operates on a single dimension, contracting over the remaining dimensions. We establish convergence guarantees in the stochastic convex setting, the proof of which builds upon matrix trace inequalities. Our experiments with state-of-the-art deep learning models show that Shampoo is capable of converging considerably faster than commonly used optimizers. Although it involves a more complex update rule, Shampoo's runtime per step is comparable to that of simple gradient methods such as SGD, AdaGrad, and Adam.
A Unified Approach to Adaptive Regularization in Online and Stochastic Optimization
Jun 20, 2017Abstract:We describe a framework for deriving and analyzing online optimization algorithms that incorporate adaptive, data-dependent regularization, also termed preconditioning. Such algorithms have been proven useful in stochastic optimization by reshaping the gradients according to the geometry of the data. Our framework captures and unifies much of the existing literature on adaptive online methods, including the AdaGrad and Online Newton Step algorithms as well as their diagonal versions. As a result, we obtain new convergence proofs for these algorithms that are substantially simpler than previous analyses. Our framework also exposes the rationale for the different preconditioned updates used in common stochastic optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge