Are All Layers Created Equal?

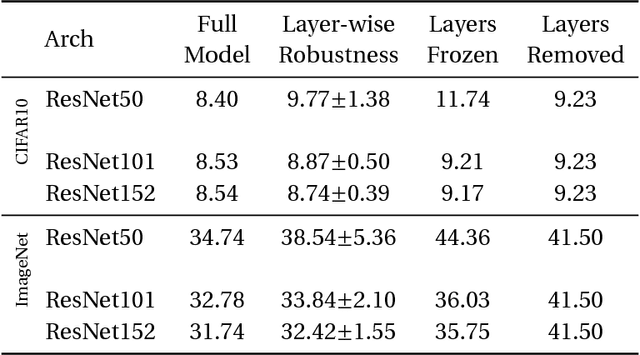
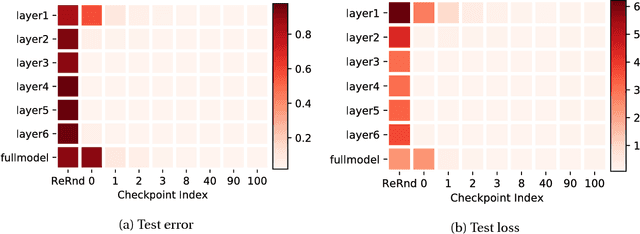
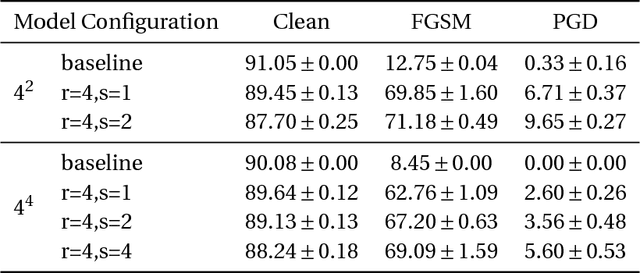
Understanding learning and generalization of deep architectures has been a major research objective in the recent years with notable theoretical progress. A main focal point of generalization studies stems from the success of excessively large networks which defy the classical wisdom of uniform convergence and learnability. We study empirically the layer-wise functional structure of overparameterized deep models. We provide evidence for the heterogeneous characteristic of layers. To do so, we introduce the notion of (post training) re-initialization and re-randomization robustness. We show that layers can be categorized into either `robust' or `critical'. In contrast to critical layers, resetting the robust layers to their initial value has no negative consequence, and in many cases they barely change throughout training. Our study provides further evidence that mere parameter counting or norm accounting is too coarse in studying generalization of deep models, and flatness or robustness analysis of the model parameters needs to respect the network architectures.