Vineet Gupta
A Computationally Efficient Sparsified Online Newton Method
Nov 16, 2023Abstract:Second-order methods hold significant promise for enhancing the convergence of deep neural network training; however, their large memory and computational demands have limited their practicality. Thus there is a need for scalable second-order methods that can efficiently train large models. In this paper, we introduce the Sparsified Online Newton (SONew) method, a memory-efficient second-order algorithm that yields a sparsified yet effective preconditioner. The algorithm emerges from a novel use of the LogDet matrix divergence measure; we combine it with sparsity constraints to minimize regret in the online convex optimization framework. Empirically, we test our method on large scale benchmarks of up to 1B parameters. We achieve up to 30% faster convergence, 3.4% relative improvement in validation performance, and 80% relative improvement in training loss, in comparison to memory efficient optimizers including first order methods. Powering the method is a surprising fact -- imposing structured sparsity patterns, like tridiagonal and banded structure, requires little to no overhead, making it as efficient and parallelizable as first-order methods. In wall-clock time, tridiagonal SONew is only about 3% slower per step than first-order methods but gives overall gains due to much faster convergence. In contrast, one of the state-of-the-art (SOTA) memory-intensive second-order methods, Shampoo, is unable to scale to large benchmarks. Additionally, while Shampoo necessitates significant engineering efforts to scale to large benchmarks, SONew offers a more straightforward implementation, increasing its practical appeal. SONew code is available at: https://github.com/devvrit/SONew
Using Foundation Models to Detect Policy Violations with Minimal Supervision
Jun 09, 2023Abstract:Foundation models, i.e. large neural networks pre-trained on large text corpora, have revolutionized NLP. They can be instructed directly (e.g. (arXiv:2005.14165)) - this is called hard prompting - and they can be tuned using very little data (e.g. (arXiv:2104.08691)) - this technique is called soft prompting. We seek to leverage their capabilities to detect policy violations. Our contributions are: We identify a hard prompt that adapts chain-of-thought prompting to policy violation tasks. This prompt produces policy violation classifications, along with extractive explanations that justify the classification. We compose the hard-prompts with soft prompt tuning to produce a classifier that attains high accuracy with very little supervision; the same classifier also produces explanations. Though the supervision only acts on the classifications, we find that the modified explanations remain consistent with the (tuned) model's response. Along the way, we identify several unintuitive aspects of foundation models. For instance, adding an example from a specific class can actually reduce predictions of that class, and separately, the effects of tokenization on scoring etc. Based on our technical results, we identify a simple workflow for product teams to quickly develop effective policy violation detectors.
Large-Scale Differentially Private BERT
Aug 03, 2021



Abstract:In this work, we study the large-scale pretraining of BERT-Large with differentially private SGD (DP-SGD). We show that combined with a careful implementation, scaling up the batch size to millions (i.e., mega-batches) improves the utility of the DP-SGD step for BERT; we also enhance its efficiency by using an increasing batch size schedule. Our implementation builds on the recent work of [SVK20], who demonstrated that the overhead of a DP-SGD step is minimized with effective use of JAX [BFH+18, FJL18] primitives in conjunction with the XLA compiler [XLA17]. Our implementation achieves a masked language model accuracy of 60.5% at a batch size of 2M, for $\epsilon = 5.36$. To put this number in perspective, non-private BERT models achieve an accuracy of $\sim$70%.
Second Order Optimization Made Practical
Feb 20, 2020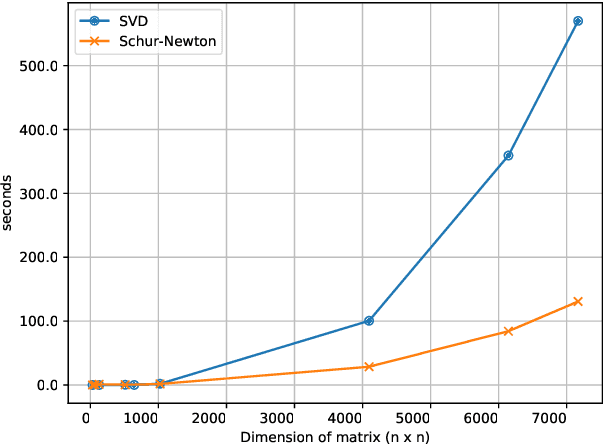

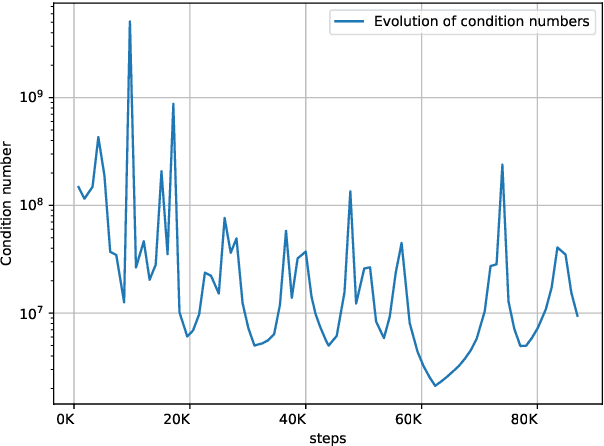

Abstract:Optimization in machine learning, both theoretical and applied, is presently dominated by first-order gradient methods such as stochastic gradient descent. Second-order optimization methods that involve second-order derivatives and/or second-order statistics of the data have become far less prevalent despite strong theoretical properties, due to their prohibitive computation, memory and communication costs. In an attempt to bridge this gap between theoretical and practical optimization, we present a proof-of-concept distributed system implementation of a second-order preconditioned method (specifically, a variant of full-matrix Adagrad), that along with a few yet critical algorithmic and numerical improvements, provides significant practical gains in convergence on state-of-the-art deep models and gives rise to actual wall-time improvements in practice compared to conventional first-order methods. Our design effectively utilizes the prevalent heterogeneous hardware architecture for training deep models which consists of a multicore CPU coupled with multiple accelerator units. We demonstrate superior performance on very large learning problems in machine translation where our distributed implementation runs considerably faster than existing gradient-based methods.
Memory-Efficient Adaptive Optimization for Large-Scale Learning
Jan 30, 2019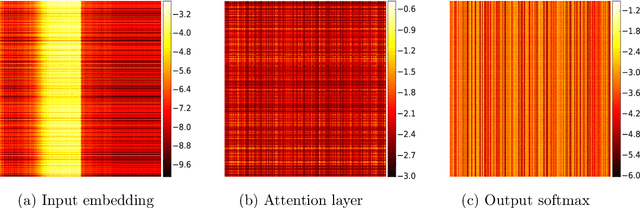
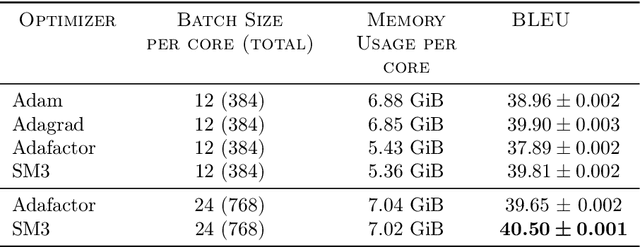
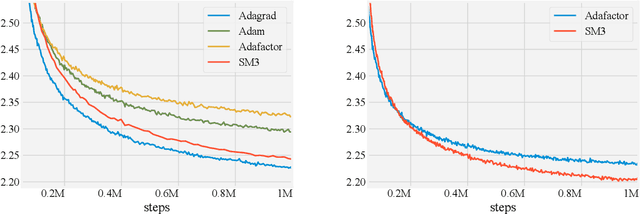
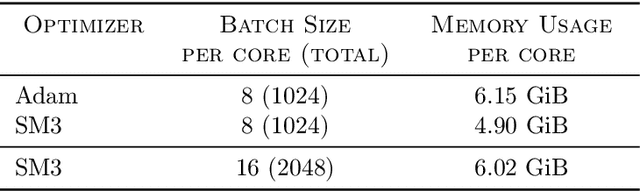
Abstract:Adaptive gradient-based optimizers such as AdaGrad and Adam are among the methods of choice in modern machine learning. These methods maintain second-order statistics of each parameter, thus doubling the memory footprint of the optimizer. In behemoth-size applications, this memory overhead restricts the size of the model being used as well as the number of examples in a mini-batch. We describe a novel, simple, and flexible adaptive optimization method with sublinear memory cost that retains the benefits of per-parameter adaptivity while allowing for larger models and mini-batches. We give convergence guarantees for our method and demonstrate its effectiveness in training very large deep models.
The Singular Values of Convolutional Layers
May 26, 2018



Abstract:We characterize the singular values of the linear transformation associated with a convolution applied to a two-dimensional feature map with multiple channels. Our characterization enables efficient computation of the singular values of convolutional layers used in popular deep neural network architectures. It also leads to an algorithm for projecting a convolutional layer onto the set of layers obeying a bound on the operator norm of the layer. We show that this is an effective regularizer; periodically applying these projections during training improves the test error of a residual network on CIFAR-10 from 6.2\% to 5.3\%.
Shampoo: Preconditioned Stochastic Tensor Optimization
Mar 02, 2018
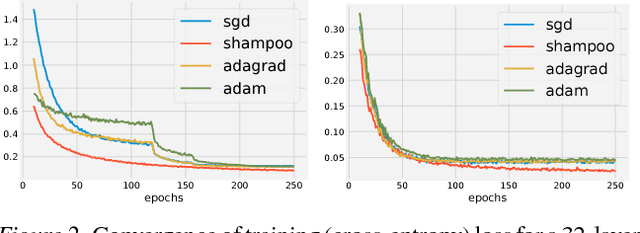
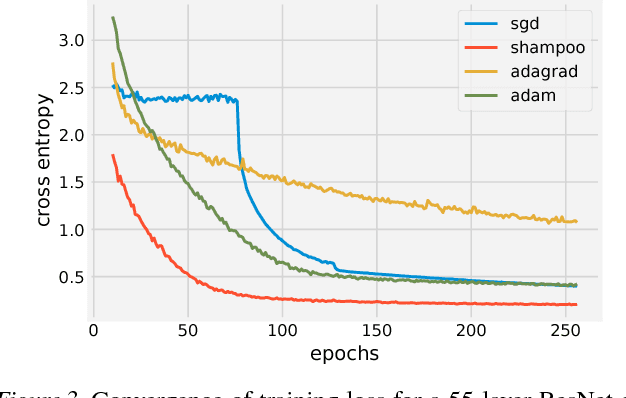
Abstract:Preconditioned gradient methods are among the most general and powerful tools in optimization. However, preconditioning requires storing and manipulating prohibitively large matrices. We describe and analyze a new structure-aware preconditioning algorithm, called Shampoo, for stochastic optimization over tensor spaces. Shampoo maintains a set of preconditioning matrices, each of which operates on a single dimension, contracting over the remaining dimensions. We establish convergence guarantees in the stochastic convex setting, the proof of which builds upon matrix trace inequalities. Our experiments with state-of-the-art deep learning models show that Shampoo is capable of converging considerably faster than commonly used optimizers. Although it involves a more complex update rule, Shampoo's runtime per step is comparable to that of simple gradient methods such as SGD, AdaGrad, and Adam.
A Unified Approach to Adaptive Regularization in Online and Stochastic Optimization
Jun 20, 2017Abstract:We describe a framework for deriving and analyzing online optimization algorithms that incorporate adaptive, data-dependent regularization, also termed preconditioning. Such algorithms have been proven useful in stochastic optimization by reshaping the gradients according to the geometry of the data. Our framework captures and unifies much of the existing literature on adaptive online methods, including the AdaGrad and Online Newton Step algorithms as well as their diagonal versions. As a result, we obtain new convergence proofs for these algorithms that are substantially simpler than previous analyses. Our framework also exposes the rationale for the different preconditioned updates used in common stochastic optimization methods.
Random Features for Compositional Kernels
Mar 22, 2017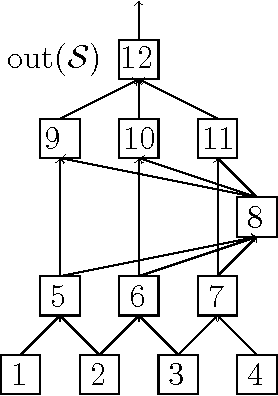
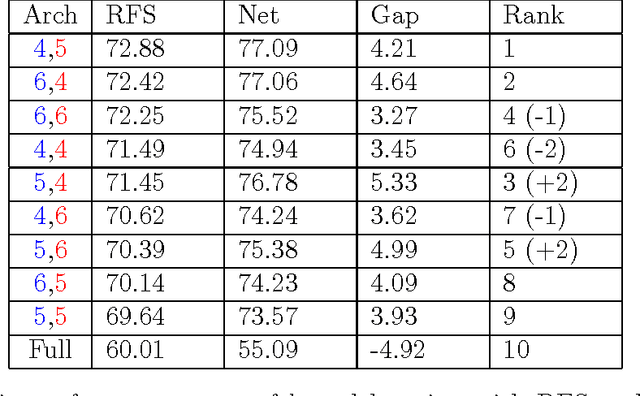
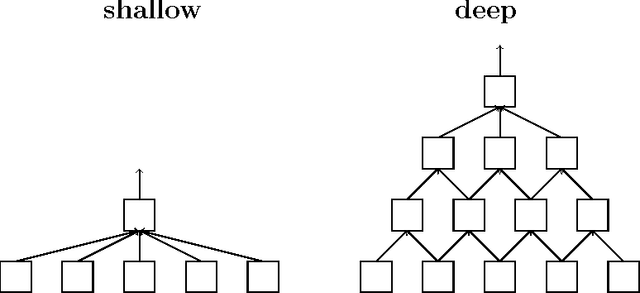
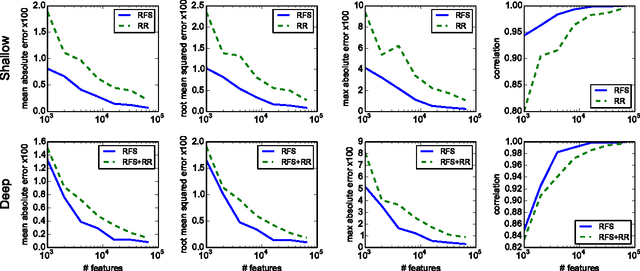
Abstract:We describe and analyze a simple random feature scheme (RFS) from prescribed compositional kernels. The compositional kernels we use are inspired by the structure of convolutional neural networks and kernels. The resulting scheme yields sparse and efficiently computable features. Each random feature can be represented as an algebraic expression over a small number of (random) paths in a composition tree. Thus, compositional random features can be stored compactly. The discrete nature of the generation process enables de-duplication of repeated features, further compacting the representation and increasing the diversity of the embeddings. Our approach complements and can be combined with previous random feature schemes.
Communicating Semantics: Reference by Description
Mar 07, 2016Abstract:Messages often refer to entities such as people, places and events. Correct identification of the intended reference is an essential part of communication. Lack of shared unique names often complicates entity reference. Shared knowledge can be used to construct uniquely identifying descriptive references for entities with ambiguous names. We introduce a mathematical model for `Reference by Description', derive results on the conditions under which, with high probability, programs can construct unambiguous references to most entities in the domain of discourse and provide empirical validation of these results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge