Gappy local conformal auto-encoders for heterogeneous data fusion: in praise of rigidity

Fusing measurements from multiple, heterogeneous, partial sources, observing a common object or process, poses challenges due to the increasing availability of numbers and types of sensors. In this work we propose, implement and validate an end-to-end computational pipeline in the form of a multiple-auto-encoder neural network architecture for this task. The inputs to the pipeline are several sets of partial observations, and the result is a globally consistent latent space, harmonizing (rigidifying, fusing) all measurements. The key enabler is the availability of multiple slightly perturbed measurements of each instance:, local measurement, "bursts", that allows us to estimate the local distortion induced by each instrument. We demonstrate the approach in a sequence of examples, starting with simple two-dimensional data sets and proceeding to a Wi-Fi localization problem and to the solution of a "dynamical puzzle" arising in spatio-temporal observations of the solutions of Partial Differential Equations.

Weakly Supervised Indoor Localization via Manifold Matching

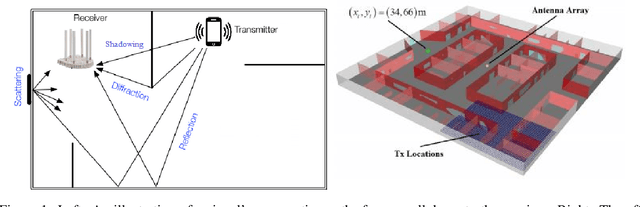
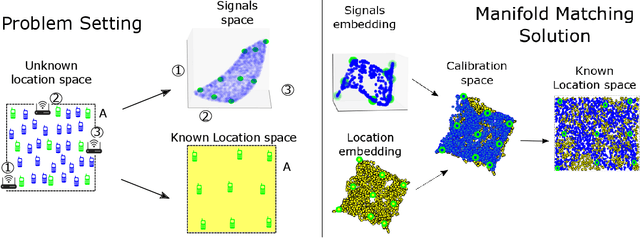
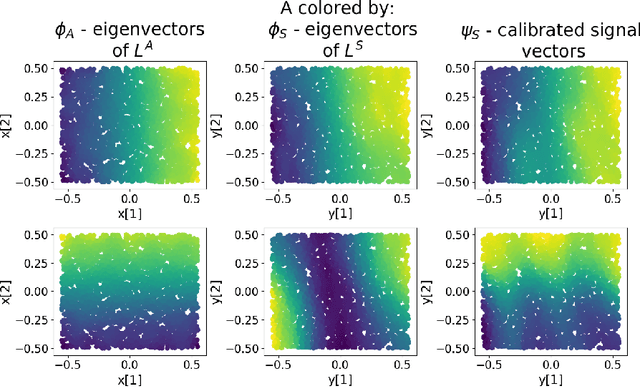
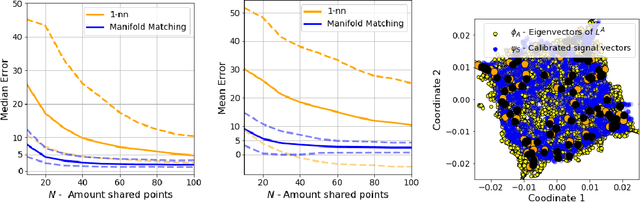
Inferring the location of a mobile device in an indoor setting is an open problem of utmost significance. A leading approach that does not require the deployment of expensive infrastructure is fingerprinting, where a classifier is trained to predict the location of a device based on its captured signal. The main caveat of this approach is that acquiring a sufficiently large and accurate training set may be prohibitively expensive. Here, we propose a weakly supervised method that only requires the location of a small number of devices. The localization is done by matching a low-dimensional spectral representation of the signals to a given sketch of the indoor environment. We test our approach on simulated and real data and show that it yields an accuracy of a few meters, which is on par with fully supervised approaches. The simplicity of our method and its accuracy with minimal supervision makes it ideal for implementation in indoor localization systems.

Let the Data Choose its Features: Differentiable Unsupervised Feature Selection

Scientific observations often consist of a large number of variables (features). Identifying a subset of meaningful features is often ignored in unsupervised learning, despite its potential for unraveling clear patterns hidden in the ambient space. In this paper, we present a method for unsupervised feature selection, tailored for the task of clustering. We propose a differentiable loss function which combines the graph Laplacian with a gating mechanism based on continuous approximation of Bernoulli random variables. The Laplacian is used to define a scoring term that favors low-frequency features, while the parameters of the Bernoulli variables are trained to enable selection of the most informative features. We mathematically motivate the proposed approach and demonstrate that in the high noise regime, it is crucial to compute the Laplacian on the gated inputs, rather than on the full feature set. Experimental demonstration of the efficacy of the proposed approach and its advantage over current baselines is provided using several real-world examples.

LOCA: LOcal Conformal Autoencoder for standardized data coordinates

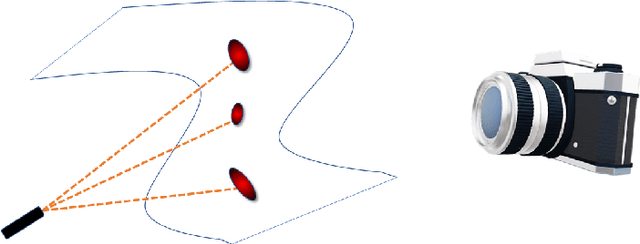
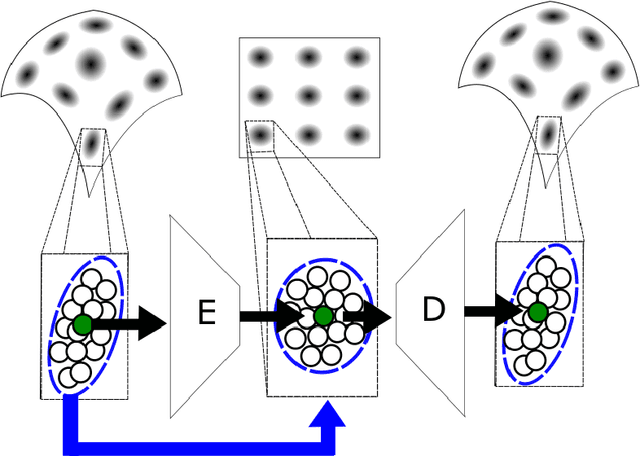
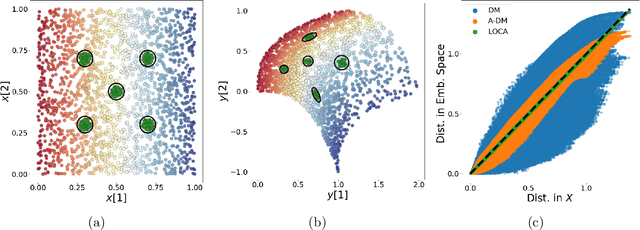
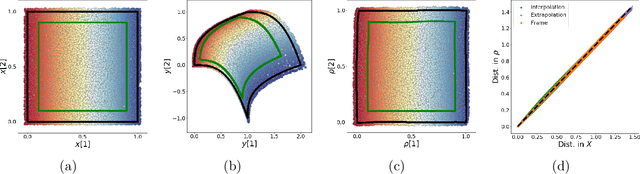
We propose a deep-learning based method for obtaining standardized data coordinates from scientific measurements.Data observations are modeled as samples from an unknown, non-linear deformation of an underlying Riemannian manifold, which is parametrized by a few normalized latent variables. By leveraging a repeated measurement sampling strategy, we present a method for learning an embedding in $\mathbb{R}^d$ that is isometric to the latent variables of the manifold. These data coordinates, being invariant under smooth changes of variables, enable matching between different instrumental observations of the same phenomenon. Our embedding is obtained using a LOcal Conformal Autoencoder (LOCA), an algorithm that constructs an embedding to rectify deformations by using a local z-scoring procedure while preserving relevant geometric information. We demonstrate the isometric embedding properties of LOCA on various model settings and observe that it exhibits promising interpolation and extrapolation capabilities. Finally, we apply LOCA to single-site Wi-Fi localization data, and to $3$-dimensional curved surface estimation based on a $2$-dimensional projection.

The Spectral Underpinning of word2vec

word2vec due to Mikolov \textit{et al.} (2013) is a word embedding method that is widely used in natural language processing. Despite its great success and frequent use, theoretical justification is still lacking. The main contribution of our paper is to propose a rigorous analysis of the highly nonlinear functional of word2vec. Our results suggest that word2vec may be primarily driven by an underlying spectral method. This insight may open the door to obtaining provable guarantees for word2vec. We support these findings by numerical simulations. One fascinating open question is whether the nonlinear properties of word2vec that are not captured by the spectral method are beneficial and, if so, by what mechanism.