Boosting Alignment for Post-Unlearning Text-to-Image Generative Models

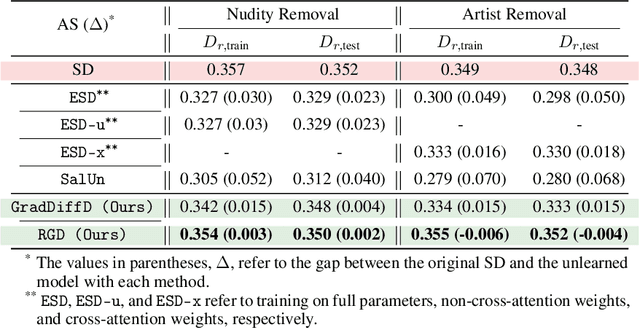
Large-scale generative models have shown impressive image-generation capabilities, propelled by massive data. However, this often inadvertently leads to the generation of harmful or inappropriate content and raises copyright concerns. Driven by these concerns, machine unlearning has become crucial to effectively purge undesirable knowledge from models. While existing literature has studied various unlearning techniques, these often suffer from either poor unlearning quality or degradation in text-image alignment after unlearning, due to the competitive nature of these objectives. To address these challenges, we propose a framework that seeks an optimal model update at each unlearning iteration, ensuring monotonic improvement on both objectives. We further derive the characterization of such an update. In addition, we design procedures to strategically diversify the unlearning and remaining datasets to boost performance improvement. Our evaluation demonstrates that our method effectively removes target classes from recent diffusion-based generative models and concepts from stable diffusion models while maintaining close alignment with the models' original trained states, thus outperforming state-of-the-art baselines. Our code will be made available at \url{https://github.com/reds-lab/Restricted_gradient_diversity_unlearning.git}.

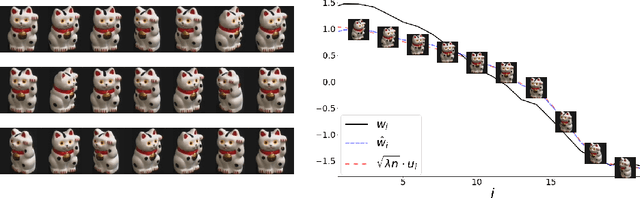
Exponential weight averaging as damped harmonic motion

The exponential moving average (EMA) is a commonly used statistic for providing stable estimates of stochastic quantities in deep learning optimization. Recently, EMA has seen considerable use in generative models, where it is computed with respect to the model weights, and significantly improves the stability of the inference model during and after training. While the practice of weight averaging at the end of training is well-studied and known to improve estimates of local optima, the benefits of EMA over the course of training is less understood. In this paper, we derive an explicit connection between EMA and a damped harmonic system between two particles, where one particle (the EMA weights) is drawn to the other (the model weights) via an idealized zero-length spring. We then leverage this physical analogy to analyze the effectiveness of EMA, and propose an improved training algorithm, which we call BELAY. Finally, we demonstrate theoretically and empirically several advantages enjoyed by BELAY over standard EMA.

The Spectral Underpinning of word2vec

word2vec due to Mikolov \textit{et al.} (2013) is a word embedding method that is widely used in natural language processing. Despite its great success and frequent use, theoretical justification is still lacking. The main contribution of our paper is to propose a rigorous analysis of the highly nonlinear functional of word2vec. Our results suggest that word2vec may be primarily driven by an underlying spectral method. This insight may open the door to obtaining provable guarantees for word2vec. We support these findings by numerical simulations. One fascinating open question is whether the nonlinear properties of word2vec that are not captured by the spectral method are beneficial and, if so, by what mechanism.