Henry Li
Source Separation by Flow Matching
May 22, 2025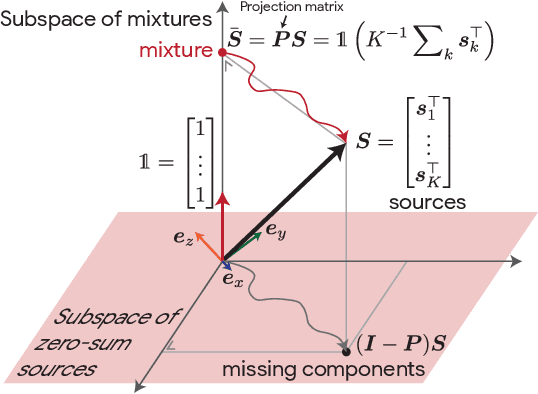
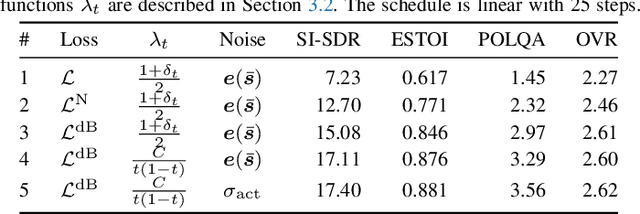
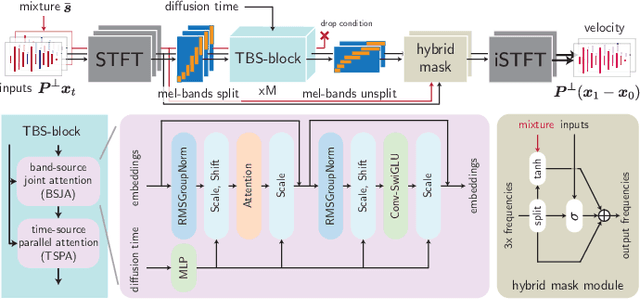
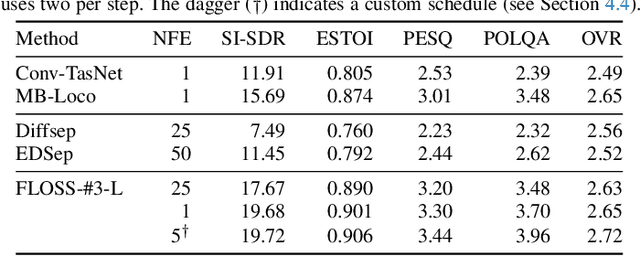
Abstract:We consider the problem of single-channel audio source separation with the goal of reconstructing $K$ sources from their mixture. We address this ill-posed problem with FLOSS (FLOw matching for Source Separation), a constrained generation method based on flow matching, ensuring strict mixture consistency. Flow matching is a general methodology that, when given samples from two probability distributions defined on the same space, learns an ordinary differential equation to output a sample from one of the distributions when provided with a sample from the other. In our context, we have access to samples from the joint distribution of $K$ sources and so the corresponding samples from the lower-dimensional distribution of their mixture. To apply flow matching, we augment these mixture samples with artificial noise components to ensure the resulting "augmented" distribution matches the dimensionality of the $K$ source distribution. Additionally, as any permutation of the sources yields the same mixture, we adopt an equivariant formulation of flow matching which relies on a suitable custom-designed neural network architecture. We demonstrate the performance of the method for the separation of overlapping speech.
Democracy of AI Numerical Weather Models: An Example of Global Forecasting with FourCastNetv2 Made by a University Research Lab Using GPU
Apr 23, 2025Abstract:This paper demonstrates the feasibility of democratizing AI-driven global weather forecasting models among university research groups by leveraging Graphics Processing Units (GPUs) and freely available AI models, such as NVIDIA's FourCastNetv2. FourCastNetv2 is an NVIDIA's advanced neural network for weather prediction and is trained on a 73-channel subset of the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5) dataset at single levels and different pressure levels. Although the training specifications for FourCastNetv2 are not released to the public, the training documentation of the model's first generation, FourCastNet, is available to all users. The training had 64 A100 GPUs and took 16 hours to complete. Although NVIDIA's models offer significant reductions in both time and cost compared to traditional Numerical Weather Prediction (NWP), reproducing published forecasting results presents ongoing challenges for resource-constrained university research groups with limited GPU availability. We demonstrate both (i) leveraging FourCastNetv2 to create predictions through the designated application programming interface (API) and (ii) utilizing NVIDIA hardware to train the original FourCastNet model. Further, this paper demonstrates the capabilities and limitations of NVIDIA A100's for resource-limited research groups in universities. We also explore data management, training efficiency, and model validation, highlighting the advantages and challenges of using limited high-performance computing resources. Consequently, this paper and its corresponding GitHub materials may serve as an initial guide for other university research groups and courses related to machine learning, climate science, and data science to develop research and education programs on AI weather forecasting, and hence help democratize the AI NWP in the digital economy.
Likelihood Training of Cascaded Diffusion Models via Hierarchical Volume-preserving Maps
Jan 13, 2025Abstract:Cascaded models are multi-scale generative models with a marked capacity for producing perceptually impressive samples at high resolutions. In this work, we show that they can also be excellent likelihood models, so long as we overcome a fundamental difficulty with probabilistic multi-scale models: the intractability of the likelihood function. Chiefly, in cascaded models each intermediary scale introduces extraneous variables that cannot be tractably marginalized out for likelihood evaluation. This issue vanishes by modeling the diffusion process on latent spaces induced by a class of transformations we call hierarchical volume-preserving maps, which decompose spatially structured data in a hierarchical fashion without introducing local distortions in the latent space. We demonstrate that two such maps are well-known in the literature for multiscale modeling: Laplacian pyramids and wavelet transforms. Not only do such reparameterizations allow the likelihood function to be directly expressed as a joint likelihood over the scales, we show that the Laplacian pyramid and wavelet transform also produces significant improvements to the state-of-the-art on a selection of benchmarks in likelihood modeling, including density estimation, lossless compression, and out-of-distribution detection. Investigating the theoretical basis of our empirical gains we uncover deep connections to score matching under the Earth Mover's Distance (EMD), which is a well-known surrogate for perceptual similarity. Code can be found at \href{https://github.com/lihenryhfl/pcdm}{this https url}.
Dual Diffusion for Unified Image Generation and Understanding
Dec 31, 2024Abstract:Diffusion models have gained tremendous success in text-to-image generation, yet still lag behind with visual understanding tasks, an area dominated by autoregressive vision-language models. We propose a large-scale and fully end-to-end diffusion model for multi-modal understanding and generation that significantly improves on existing diffusion-based multimodal models, and is the first of its kind to support the full suite of vision-language modeling capabilities. Inspired by the multimodal diffusion transformer (MM-DiT) and recent advances in discrete diffusion language modeling, we leverage a cross-modal maximum likelihood estimation framework that simultaneously trains the conditional likelihoods of both images and text jointly under a single loss function, which is back-propagated through both branches of the diffusion transformer. The resulting model is highly flexible and capable of a wide range of tasks including image generation, captioning, and visual question answering. Our model attained competitive performance compared to recent unified image understanding and generation models, demonstrating the potential of multimodal diffusion modeling as a promising alternative to autoregressive next-token prediction models.
Solving Inverse Problems via Diffusion Optimal Control
Dec 21, 2024Abstract:Existing approaches to diffusion-based inverse problem solvers frame the signal recovery task as a probabilistic sampling episode, where the solution is drawn from the desired posterior distribution. This framework suffers from several critical drawbacks, including the intractability of the conditional likelihood function, strict dependence on the score network approximation, and poor $\mathbf{x}_0$ prediction quality. We demonstrate that these limitations can be sidestepped by reframing the generative process as a discrete optimal control episode. We derive a diffusion-based optimal controller inspired by the iterative Linear Quadratic Regulator (iLQR) algorithm. This framework is fully general and able to handle any differentiable forward measurement operator, including super-resolution, inpainting, Gaussian deblurring, nonlinear deblurring, and even highly nonlinear neural classifiers. Furthermore, we show that the idealized posterior sampling equation can be recovered as a special case of our algorithm. We then evaluate our method against a selection of neural inverse problem solvers, and establish a new baseline in image reconstruction with inverse problems.
Non-Normal Diffusion Models
Dec 10, 2024Abstract:Diffusion models generate samples by incrementally reversing a process that turns data into noise. We show that when the step size goes to zero, the reversed process is invariant to the distribution of these increments. This reveals a previously unconsidered parameter in the design of diffusion models: the distribution of the diffusion step $\Delta x_k := x_{k} - x_{k + 1}$. This parameter is implicitly set by default to be normally distributed in most diffusion models. By lifting this assumption, we generalize the framework for designing diffusion models and establish an expanded class of diffusion processes with greater flexibility in the choice of loss function used during training. We demonstrate the effectiveness of these models on density estimation and generative modeling tasks on standard image datasets, and show that different choices of the distribution of $\Delta x_k$ result in qualitatively different generated samples.
Boosting Alignment for Post-Unlearning Text-to-Image Generative Models
Dec 09, 2024

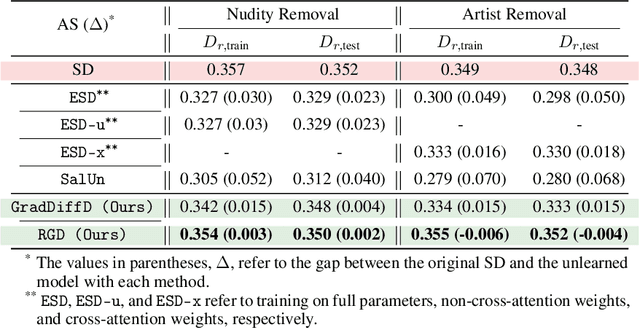

Abstract:Large-scale generative models have shown impressive image-generation capabilities, propelled by massive data. However, this often inadvertently leads to the generation of harmful or inappropriate content and raises copyright concerns. Driven by these concerns, machine unlearning has become crucial to effectively purge undesirable knowledge from models. While existing literature has studied various unlearning techniques, these often suffer from either poor unlearning quality or degradation in text-image alignment after unlearning, due to the competitive nature of these objectives. To address these challenges, we propose a framework that seeks an optimal model update at each unlearning iteration, ensuring monotonic improvement on both objectives. We further derive the characterization of such an update. In addition, we design procedures to strategically diversify the unlearning and remaining datasets to boost performance improvement. Our evaluation demonstrates that our method effectively removes target classes from recent diffusion-based generative models and concepts from stable diffusion models while maintaining close alignment with the models' original trained states, thus outperforming state-of-the-art baselines. Our code will be made available at \url{https://github.com/reds-lab/Restricted_gradient_diversity_unlearning.git}.
Exponential weight averaging as damped harmonic motion
Oct 20, 2023Abstract:The exponential moving average (EMA) is a commonly used statistic for providing stable estimates of stochastic quantities in deep learning optimization. Recently, EMA has seen considerable use in generative models, where it is computed with respect to the model weights, and significantly improves the stability of the inference model during and after training. While the practice of weight averaging at the end of training is well-studied and known to improve estimates of local optima, the benefits of EMA over the course of training is less understood. In this paper, we derive an explicit connection between EMA and a damped harmonic system between two particles, where one particle (the EMA weights) is drawn to the other (the model weights) via an idealized zero-length spring. We then leverage this physical analogy to analyze the effectiveness of EMA, and propose an improved training algorithm, which we call BELAY. Finally, we demonstrate theoretically and empirically several advantages enjoyed by BELAY over standard EMA.
Anomaly Detection with Variance Stabilized Density Estimation
Jun 01, 2023Abstract:Density estimation based anomaly detection schemes typically model anomalies as examples that reside in low-density regions. We propose a modified density estimation problem and demonstrate its effectiveness for anomaly detection. Specifically, we assume the density function of normal samples is uniform in some compact domain. This assumption implies the density function is more stable (with lower variance) around normal samples than anomalies. We first corroborate this assumption empirically using a wide range of real-world data. Then, we design a variance stabilized density estimation problem for maximizing the likelihood of the observed samples while minimizing the variance of the density around normal samples. We introduce an ensemble of autoregressive models to learn the variance stabilized distribution. Finally, we perform an extensive benchmark with 52 datasets demonstrating that our method leads to state-of-the-art results while alleviating the need for data-specific hyperparameter tuning.
Autoregressive Generative Modeling with Noise Conditional Maximum Likelihood Estimation
Oct 19, 2022
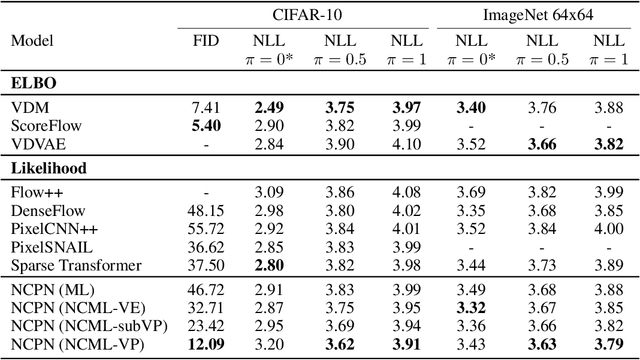


Abstract:We introduce a simple modification to the standard maximum likelihood estimation (MLE) framework. Rather than maximizing a single unconditional likelihood of the data under the model, we maximize a family of \textit{noise conditional} likelihoods consisting of the data perturbed by a continuum of noise levels. We find that models trained this way are more robust to noise, obtain higher test likelihoods, and generate higher quality images. They can also be sampled from via a novel score-based sampling scheme which combats the classical \textit{covariate shift} problem that occurs during sample generation in autoregressive models. Applying this augmentation to autoregressive image models, we obtain 3.32 bits per dimension on the ImageNet 64x64 dataset, and substantially improve the quality of generated samples in terms of the Frechet Inception distance (FID) -- from 37.50 to 12.09 on the CIFAR-10 dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge