Neural Network Architectures for Stochastic Control using the Nonlinear Feynman-Kac Lemma

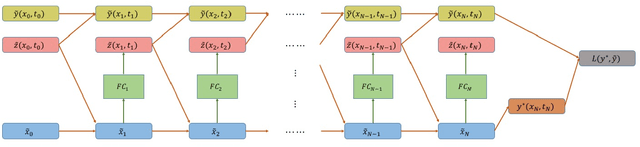
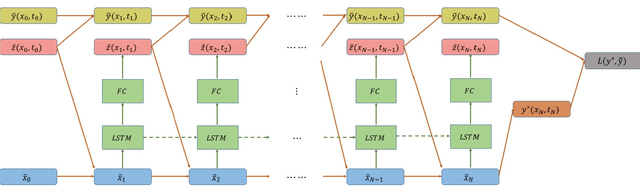
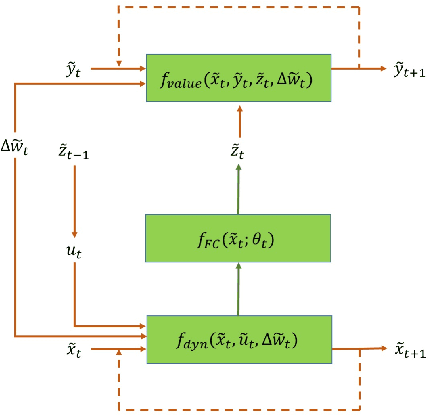
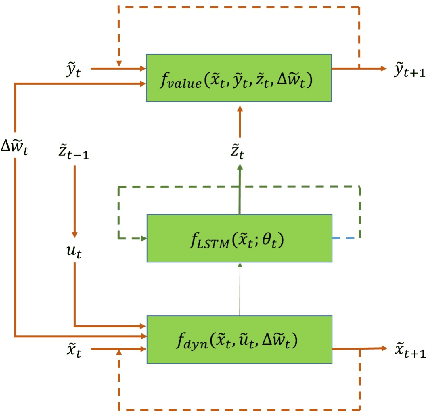
In this paper we propose a new methodology for decision-making under uncertainty using recent advancements in the areas of nonlinear stochastic optimal control theory, applied mathematics and machine learning. Our work is grounded on the nonlinear Feynman-Kac lemma and the fundamental connection between backward nonlinear partial differential equations and forward-backward stochastic differential equations. Using these connections and results from our prior work on importance sampling for forward-backward stochastic differential equations, we develop a control framework that is scalable and applicable to general classes of stochastic systems and decision-making problem formulations in robotics and autonomy. Two architectures for stochastic control are proposed that consist of feed-forward and recurrent neural networks. The performance and scalability of the aforementioned algorithms is investigated in two stochastic optimal control problem formulations including the unconstrained L2 and control-constrained case, and three systems in simulation. We conclude with a discussion on the implications of the proposed algorithms to robotics and autonomous systems.

MPC-Inspired Neural Network Policies for Sequential Decision Making

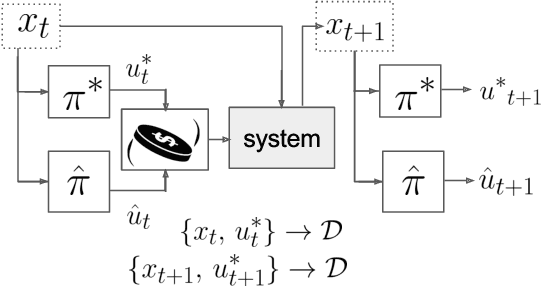
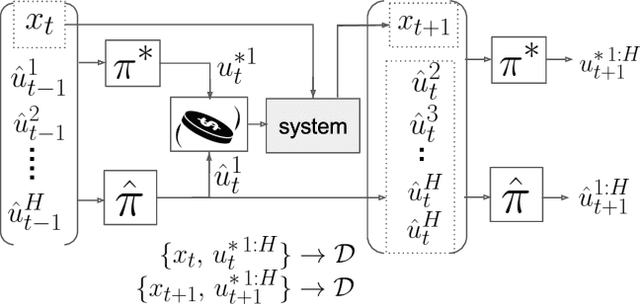
In this paper we investigate the use of MPC-inspired neural network policies for sequential decision making. We introduce an extension to the DAgger algorithm for training such policies and show how they have improved training performance and generalization capabilities. We take advantage of this extension to show scalable and efficient training of complex planning policy architectures in continuous state and action spaces. We provide an extensive comparison of neural network policies by considering feed forward policies, recurrent policies, and recurrent policies with planning structure inspired by the Path Integral control framework. Our results suggest that MPC-type recurrent policies have better robustness to disturbances and modeling error.