Ioannis Exarchos
Deep $\mathcal{L}^1$ Stochastic Optimal Control Policies for Planetary Soft-landing
Sep 01, 2021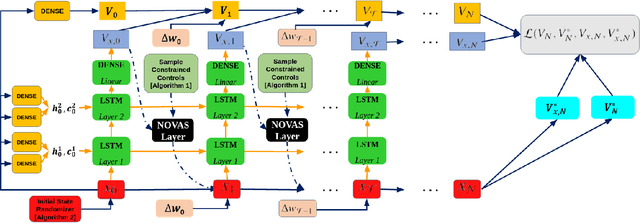

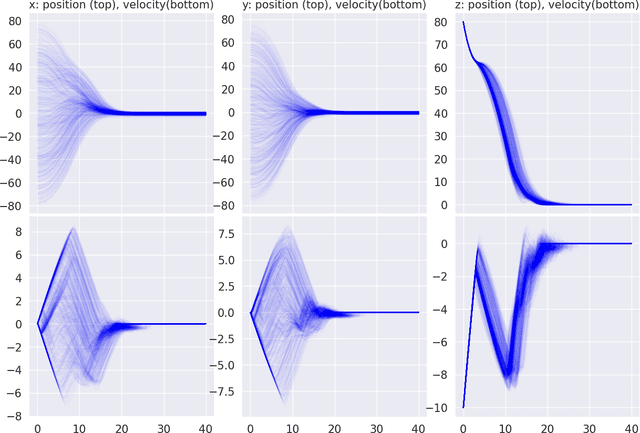
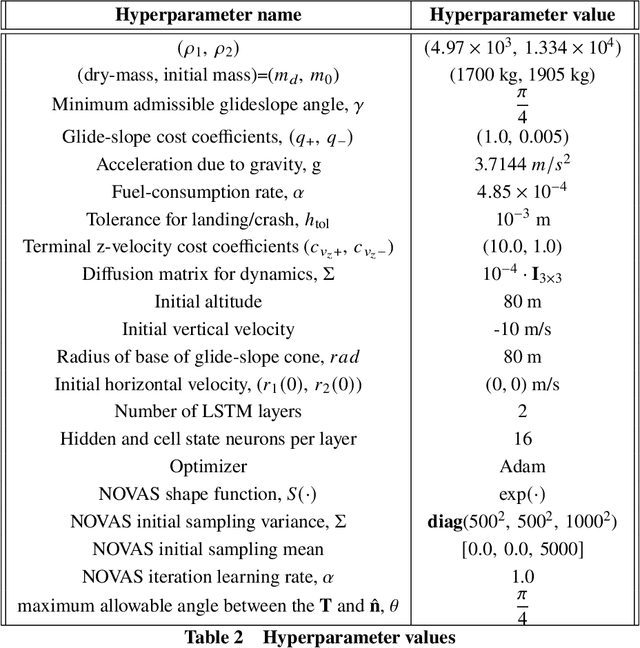
Abstract:In this paper, we introduce a novel deep learning based solution to the Powered-Descent Guidance (PDG) problem, grounded in principles of nonlinear Stochastic Optimal Control (SOC) and Feynman-Kac theory. Our algorithm solves the PDG problem by framing it as an $\mathcal{L}^1$ SOC problem for minimum fuel consumption. Additionally, it can handle practically useful control constraints, nonlinear dynamics and enforces state constraints as soft-constraints. This is achieved by building off of recent work on deep Forward-Backward Stochastic Differential Equations (FBSDEs) and differentiable non-convex optimization neural-network layers based on stochastic search. In contrast to previous approaches, our algorithm does not require convexification of the constraints or linearization of the dynamics and is empirically shown to be robust to stochastic disturbances and the initial position of the spacecraft. After training offline, our controller can be activated once the spacecraft is within a pre-specified radius of the landing zone and at a pre-specified altitude i.e., the base of an inverted cone with the tip at the landing zone. We demonstrate empirically that our controller can successfully and safely land all trajectories initialized at the base of this cone while minimizing fuel consumption.
DASH: Modularized Human Manipulation Simulation with Vision and Language for Embodied AI
Aug 28, 2021

Abstract:Creating virtual humans with embodied, human-like perceptual and actuation constraints has the promise to provide an integrated simulation platform for many scientific and engineering applications. We present Dynamic and Autonomous Simulated Human (DASH), an embodied virtual human that, given natural language commands, performs grasp-and-stack tasks in a physically-simulated cluttered environment solely using its own visual perception, proprioception, and touch, without requiring human motion data. By factoring the DASH system into a vision module, a language module, and manipulation modules of two skill categories, we can mix and match analytical and machine learning techniques for different modules so that DASH is able to not only perform randomly arranged tasks with a high success rate, but also do so under anthropomorphic constraints and with fluid and diverse motions. The modular design also favors analysis and extensibility to more complex manipulation skills.
* SCA'2021
Fast and Feature-Complete Differentiable Physics for Articulated Rigid Bodies with Contact
Apr 01, 2021
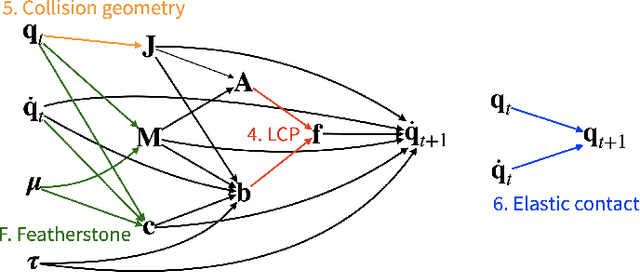
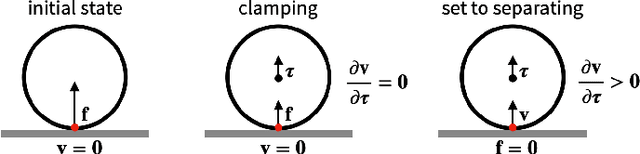
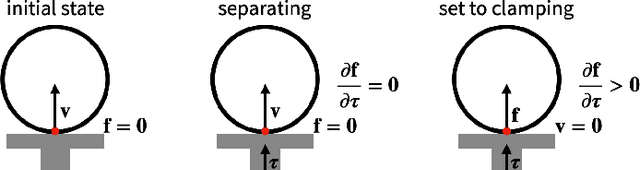
Abstract:We present a fast and feature-complete differentiable physics engine that supports Lagrangian dynamics and hard contact constraints for articulated rigid body simulation. Our differentiable physics engine offers a complete set of features that are typically only available in non-differentiable physics simulators commonly used by robotics applications. We solve contact constraints precisely using linear complementarity problems (LCPs). We present efficient and novel analytical gradients through the LCP formulation of inelastic contact that exploit the sparsity of the LCP solution. We support complex contact geometry, and gradients approximating continuous-time elastic collision. We also introduce a novel method to compute complementarity-aware gradients that help downstream optimization tasks avoid stalling in saddle points. We show that an implementation of this combination in an existing physics engine (DART) is capable of a 45x single-core speedup over finite-differencing in computing analytical Jacobians for a single timestep, while preserving all the expressiveness of original DART.
Task-Specific Design Optimization and Fabrication for Inflated-Beam Soft Robots with Growable Discrete Joints
Mar 08, 2021
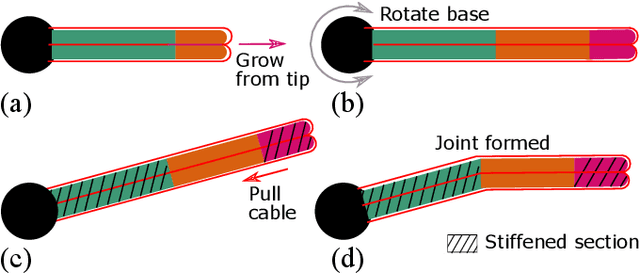
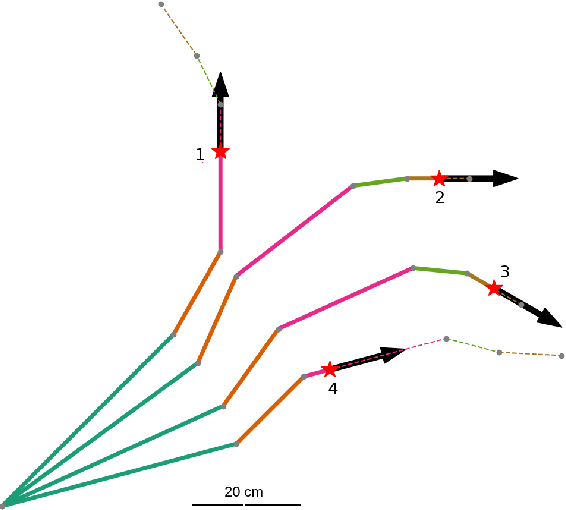
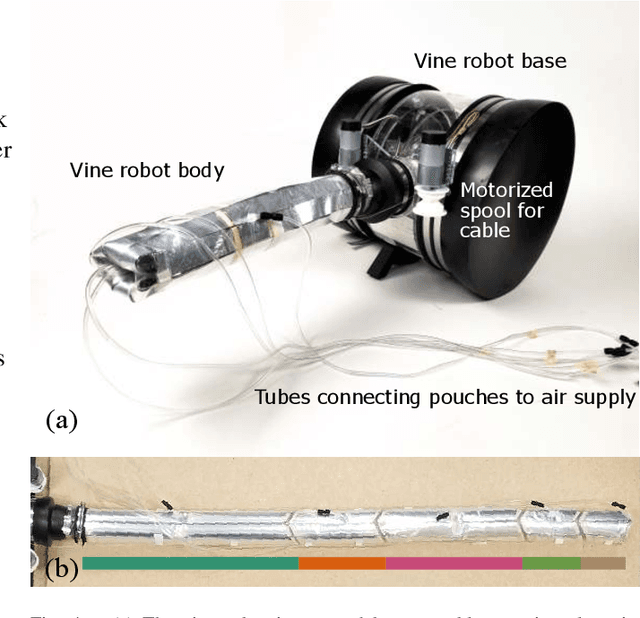
Abstract:Soft robot serial chain manipulators with the capability for growth, stiffness control, and discrete joints have the potential to approach the dexterity of traditional robot arms, while improving safety, lowering cost, and providing an increased workspace, with potential application in home environments. This paper presents an approach for design optimization of such robots to reach specified targets while minimizing the number of discrete joints and thus construction and actuation costs. We define a maximum number of allowable joints, as well as hardware constraints imposed by the materials and actuation available for soft growing robots, and we formulate and solve an optimization problem to output a robot design, i.e., the total number of potential joints and their locations along the robot body, which reaches all the desired targets. We then rapidly construct the resulting soft growing robot design using readily available, low-cost materials, and we demonstrate its ability to reach the desired targets. Finally, we use our algorithm to evaluate the ability of this design to reach new targets, and we demonstrate the algorithm's utility as a design tool to explore robot capabilities given various constraints and objectives.
Multi-agent Deep FBSDE Representation For Large Scale Stochastic Differential Games
Nov 21, 2020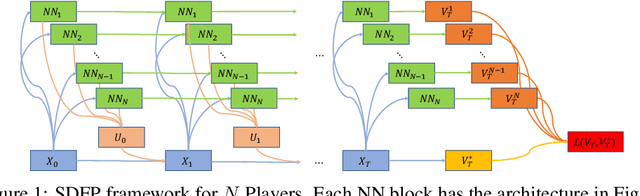

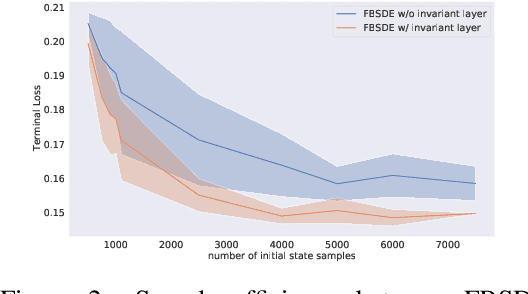
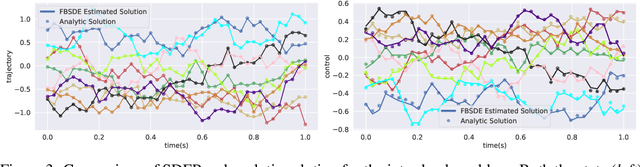
Abstract:In this paper, we present a deep learning framework for solving large-scale multi-agent non-cooperative stochastic games using fictitious play. The Hamilton-Jacobi-Bellman (HJB) PDE associated with each agent is reformulated into a set of Forward-Backward Stochastic Differential Equations (FBSDEs) and solved via forward sampling on a suitably defined neural network architecture. Decision-making in multi-agent systems suffers from the curse of dimensionality and strategy degeneration as the number of agents and time horizon increase. We propose a novel Deep FBSDE controller framework which is shown to outperform the current state-of-the-art deep fictitious play algorithm on a high dimensional inter-bank lending/borrowing problem. More importantly, our approach mitigates the curse of many agents and reduces computational and memory complexity, allowing us to scale up to 1,000 agents in simulation, a scale which, to the best of our knowledge, represents a new state of the art. Finally, we showcase the framework's applicability in robotics on a belief-space autonomous racing problem.
Policy Transfer via Kinematic Domain Randomization and Adaptation
Nov 03, 2020

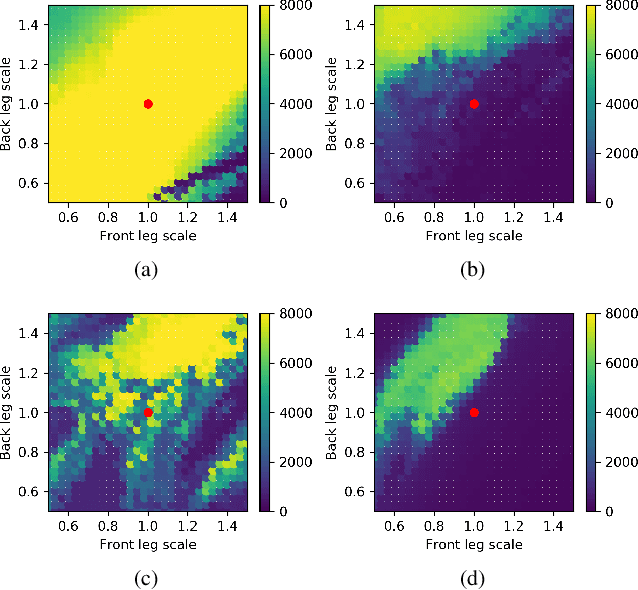
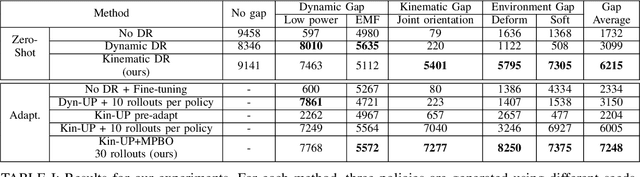
Abstract:Transferring reinforcement learning policies trained in physics simulation to the real hardware remains a challenge, known as the "sim-to-real" gap. Domain randomization is a simple yet effective technique to address dynamics discrepancies across source and target domains, but its success generally depends on heuristics and trial-and-error. In this work we investigate the impact of randomized parameter selection on policy transferability across different types of domain discrepancies. Contrary to common practice in which kinematic parameters are carefully measured while dynamic parameters are randomized, we found that virtually randomizing kinematic parameters (e.g., link lengths) during training in simulation generally outperforms dynamic randomization. Based on this finding, we introduce a new domain adaptation algorithm that utilizes simulated kinematic parameters variation. Our algorithm, Multi-Policy Bayesian Optimization, trains an ensemble of universal policies conditioned on virtual kinematic parameters and efficiently adapts to the target environment using a limited number of target domain rollouts. We showcase our findings on a simulated quadruped robot in five different target environments covering different aspects of domain discrepancies.
Safe Optimal Control Using Stochastic Barrier Functions and Deep Forward-Backward SDEs
Sep 02, 2020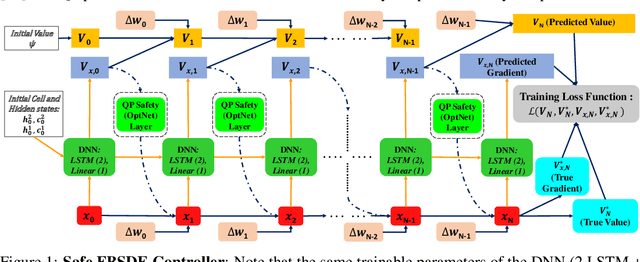
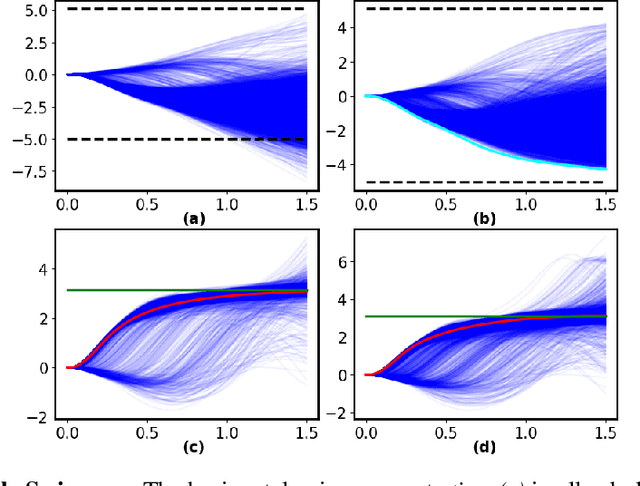
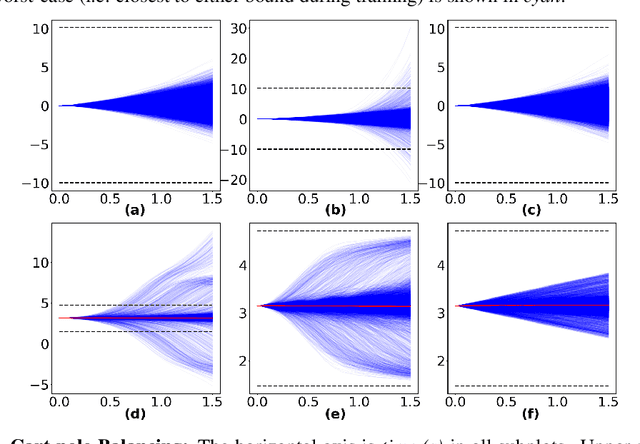
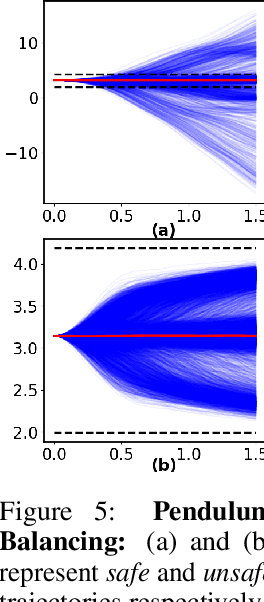
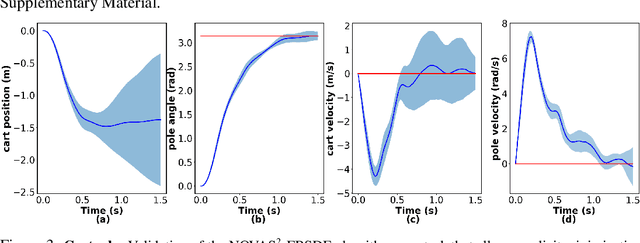
Abstract:This paper introduces a new formulation for stochastic optimal control and stochastic dynamic optimization that ensures safety with respect to state and control constraints. The proposed methodology brings together concepts such as Forward-Backward Stochastic Differential Equations, Stochastic Barrier Functions, Differentiable Convex Optimization and Deep Learning. Using the aforementioned concepts, a Neural Network architecture is designed for safe trajectory optimization in which learning can be performed in an end-to-end fashion. Simulations are performed on three systems to show the efficacy of the proposed methodology.
Non-convex Optimization via Adaptive Stochastic Search for End-to-End Learning and Control
Jun 22, 2020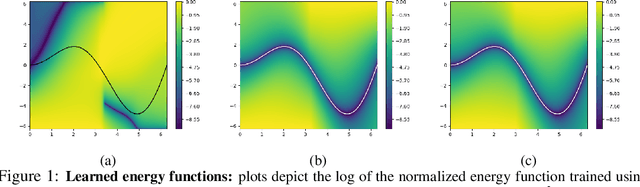
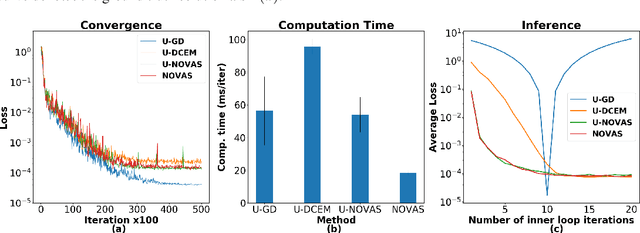
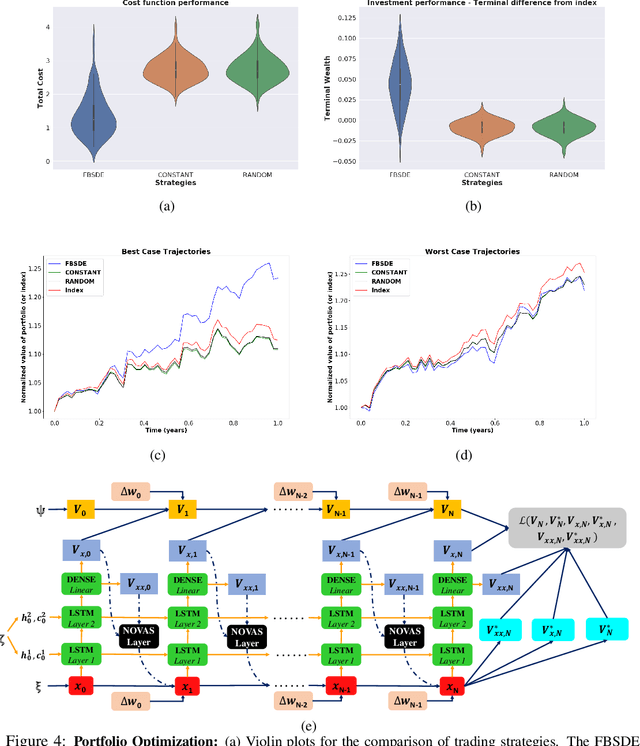
Abstract:In this work we propose the use of adaptive stochastic search as a building block for general, non-convex optimization operations within deep neural network architectures. Specifically, for an objective function located at some layer in the network and parameterized by some network parameters, we employ adaptive stochastic search to perform optimization over its output. This operation is differentiable and does not obstruct the passing of gradients during backpropagation, thus enabling us to incorporate it as a component in end-to-end learning. We study the proposed optimization module's properties and benchmark it against two existing alternatives on a synthetic energy-based structured prediction task, and further showcase its use in stochastic optimal control applications.
Deep Forward-Backward SDEs for Min-max Control
Jun 11, 2019
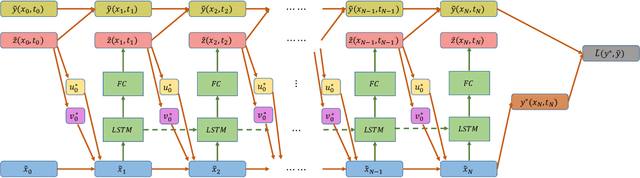
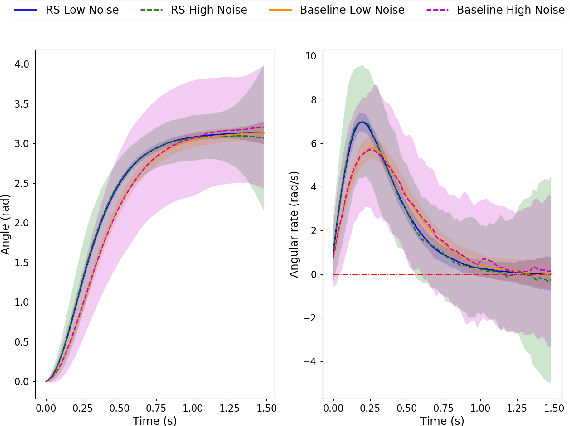
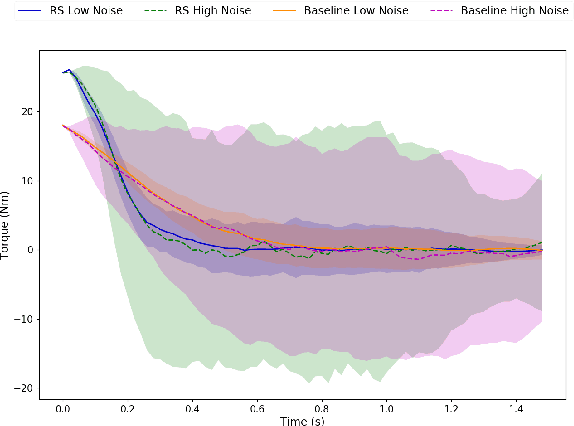
Abstract:This paper presents a novel approach to numerically solve stochastic differential games for nonlinear systems. The proposed approach relies on the nonlinear Feynman-Kac theorem that establishes a connection between parabolic deterministic partial differential equations and forward-backward stochastic differential equations. Using this theorem the Hamilton-Jacobi-Isaacs partial differential equation associated with differential games is represented by a system of forward-backward stochastic differential equations. Numerical solution of the aforementioned system of stochastic differential equations is performed using importance sampling and a Long-Short Term Memory recurrent neural network, which is trained in an offline fashion. The resulting algorithm is tested on two example systems in simulation and compared against the standard risk neutral stochastic optimal control formulations.
Neural Network Architectures for Stochastic Control using the Nonlinear Feynman-Kac Lemma
Feb 18, 2019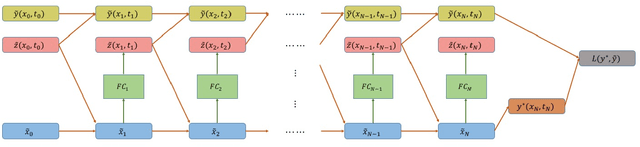
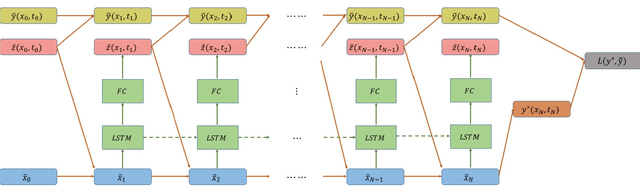
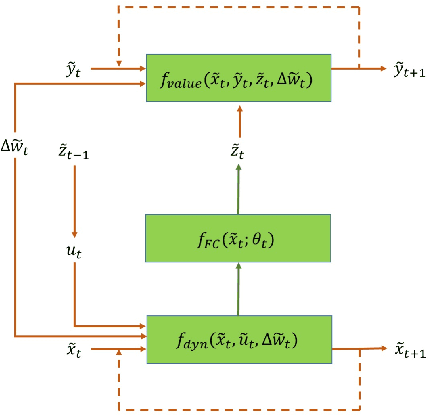
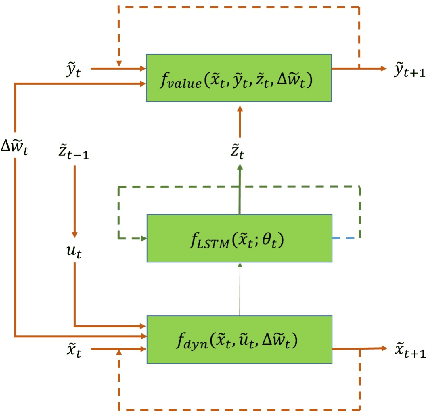
Abstract:In this paper we propose a new methodology for decision-making under uncertainty using recent advancements in the areas of nonlinear stochastic optimal control theory, applied mathematics and machine learning. Our work is grounded on the nonlinear Feynman-Kac lemma and the fundamental connection between backward nonlinear partial differential equations and forward-backward stochastic differential equations. Using these connections and results from our prior work on importance sampling for forward-backward stochastic differential equations, we develop a control framework that is scalable and applicable to general classes of stochastic systems and decision-making problem formulations in robotics and autonomy. Two architectures for stochastic control are proposed that consist of feed-forward and recurrent neural networks. The performance and scalability of the aforementioned algorithms is investigated in two stochastic optimal control problem formulations including the unconstrained L2 and control-constrained case, and three systems in simulation. We conclude with a discussion on the implications of the proposed algorithms to robotics and autonomous systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge