Fast and Feature-Complete Differentiable Physics for Articulated Rigid Bodies with Contact

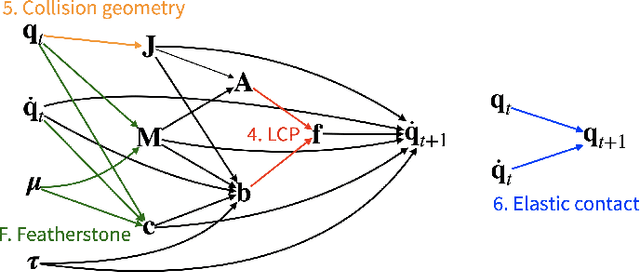
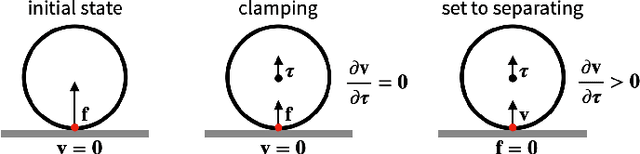
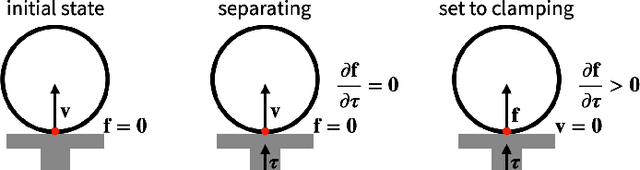
We present a fast and feature-complete differentiable physics engine that supports Lagrangian dynamics and hard contact constraints for articulated rigid body simulation. Our differentiable physics engine offers a complete set of features that are typically only available in non-differentiable physics simulators commonly used by robotics applications. We solve contact constraints precisely using linear complementarity problems (LCPs). We present efficient and novel analytical gradients through the LCP formulation of inelastic contact that exploit the sparsity of the LCP solution. We support complex contact geometry, and gradients approximating continuous-time elastic collision. We also introduce a novel method to compute complementarity-aware gradients that help downstream optimization tasks avoid stalling in saddle points. We show that an implementation of this combination in an existing physics engine (DART) is capable of a 45x single-core speedup over finite-differencing in computing analytical Jacobians for a single timestep, while preserving all the expressiveness of original DART.

Bayesian Policy Optimization for Model Uncertainty

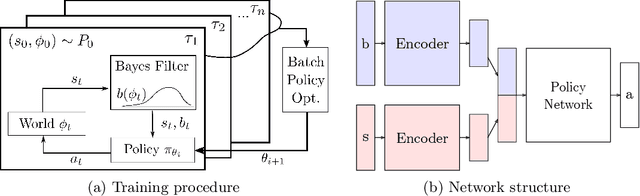
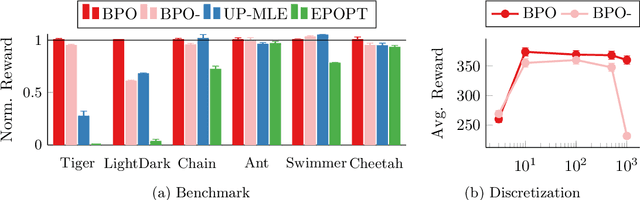
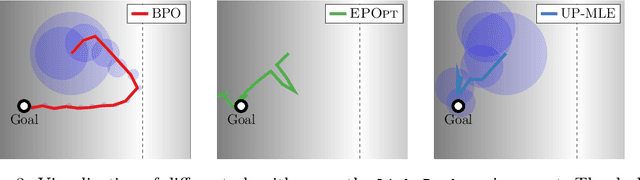
Addressing uncertainty is critical for autonomous systems to robustly adapt to the real world. We formulate the problem of model uncertainty as a continuous Bayes-Adaptive Markov Decision Process (BAMDP), where an agent maintains a posterior distribution over the latent model parameters given a history of observations and maximizes its expected long-term reward with respect to this belief distribution. Our algorithm, Bayesian Policy Optimization, builds on recent policy optimization algorithms to learn a universal policy that navigates the exploration-exploitation trade-off to maximize the Bayesian value function. To address challenges from discretizing the continuous latent parameter space, we propose a policy network architecture that independently encodes the belief distribution from the observable state. Our method significantly outperforms algorithms that address model uncertainty without explicitly reasoning about belief distributions, and is competitive with state-of-the-art Partially Observable Markov Decision Process solvers.

A Linear-Time Variational Integrator for Multibody Systems

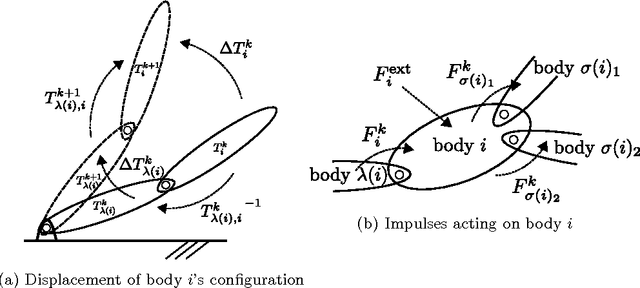
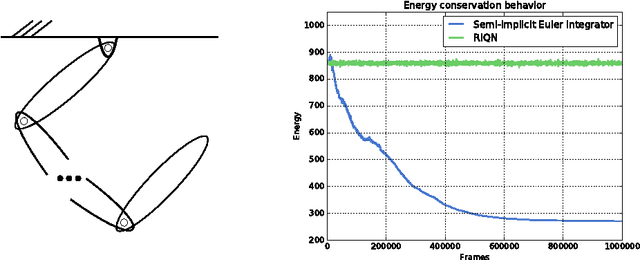
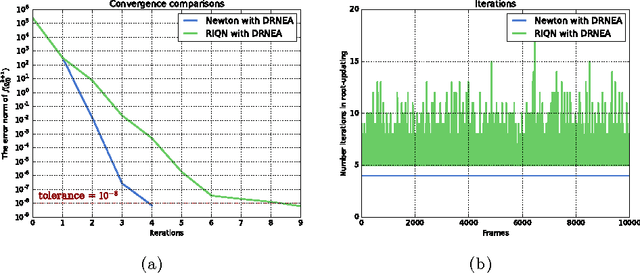
We present an efficient variational integrator for multibody systems. Variational integrators reformulate the equations of motion for multibody systems as discrete Euler-Lagrange (DEL) equations, transforming forward integration into a root-finding problem for the DEL equations. Variational integrators have been shown to be more robust and accurate in preserving fundamental properties of systems, such as momentum and energy, than many frequently used numerical integrators. However, state-of-the-art algorithms suffer from $O(n^3)$ complexity, which is prohibitive for articulated multibody systems with a large number of degrees of freedom, $n$, in generalized coordinates. Our key contribution is to derive a recursive algorithm that evaluates DEL equations in $O(n)$, which scales up well for complex multibody systems such as humanoid robots. Inspired by recursive Newton-Euler algorithm, our key insight is to formulate DEL equation individually for each body rather than for the entire system. Furthermore, we introduce a new quasi-Newton method that exploits the impulse-based dynamics algorithm, which is also $O(n)$, to avoid the expensive Jacobian inversion in solving DEL equations. We demonstrate scalability and efficiency, as well as extensibility to holonomic constraints through several case studies.