Bayesian Policy Optimization for Model Uncertainty

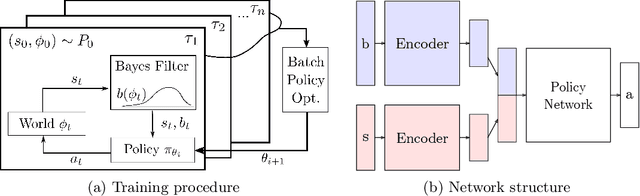
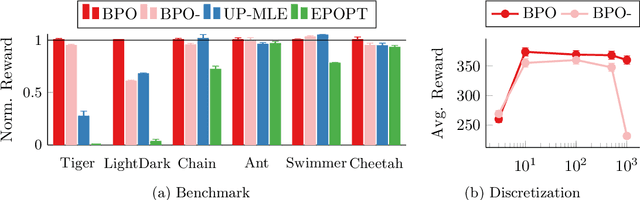
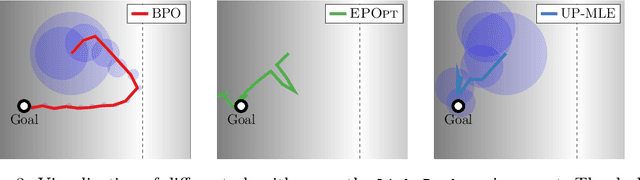
Addressing uncertainty is critical for autonomous systems to robustly adapt to the real world. We formulate the problem of model uncertainty as a continuous Bayes-Adaptive Markov Decision Process (BAMDP), where an agent maintains a posterior distribution over the latent model parameters given a history of observations and maximizes its expected long-term reward with respect to this belief distribution. Our algorithm, Bayesian Policy Optimization, builds on recent policy optimization algorithms to learn a universal policy that navigates the exploration-exploitation trade-off to maximize the Bayesian value function. To address challenges from discretizing the continuous latent parameter space, we propose a policy network architecture that independently encodes the belief distribution from the observable state. Our method significantly outperforms algorithms that address model uncertainty without explicitly reasoning about belief distributions, and is competitive with state-of-the-art Partially Observable Markov Decision Process solvers.