Multi-Sample Long Range Path Planning under Sensing Uncertainty for Off-Road Autonomous Driving

We focus on the problem of long-range dynamic replanning for off-road autonomous vehicles, where a robot plans paths through a previously unobserved environment while continuously receiving noisy local observations. An effective approach for planning under sensing uncertainty is determinization, where one converts a stochastic world into a deterministic one and plans under this simplification. This makes the planning problem tractable, but the cost of following the planned path in the real world may be different than in the determinized world. This causes collisions if the determinized world optimistically ignores obstacles, or causes unnecessarily long routes if the determinized world pessimistically imagines more obstacles. We aim to be robust to uncertainty over potential worlds while still achieving the efficiency benefits of determinization. We evaluate algorithms for dynamic replanning on a large real-world dataset of challenging long-range planning problems from the DARPA RACER program. Our method, Dynamic Replanning via Evaluating and Aggregating Multiple Samples (DREAMS), outperforms other determinization-based approaches in terms of combined traversal time and collision cost. https://sites.google.com/cs.washington.edu/dreams/

Stein Variational Probabilistic Roadmaps

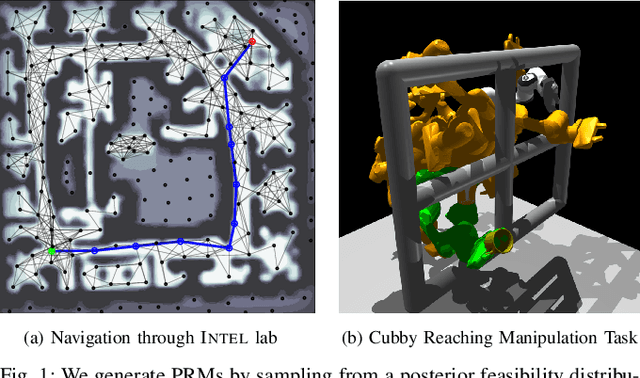
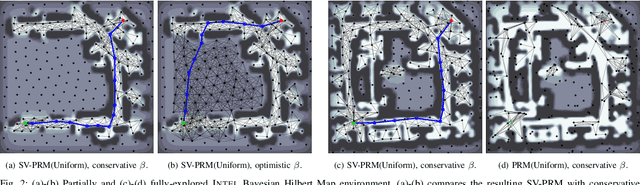
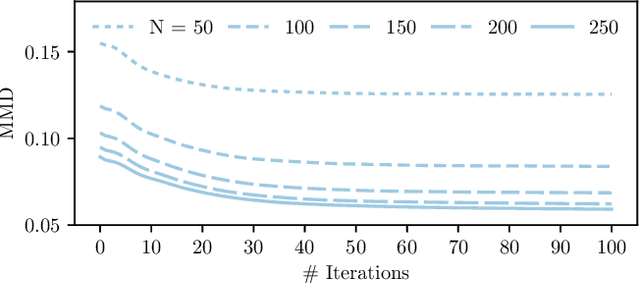
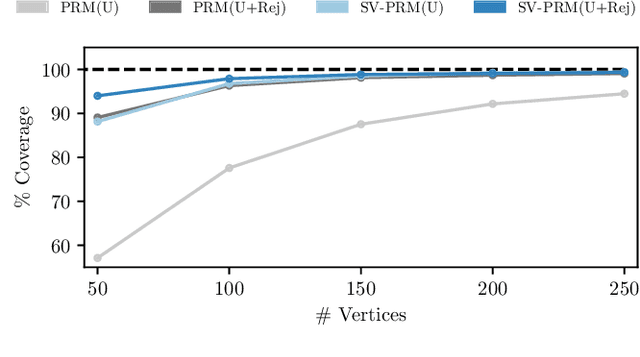
Efficient and reliable generation of global path plans are necessary for safe execution and deployment of autonomous systems. In order to generate planning graphs which adequately resolve the topology of a given environment, many sampling-based motion planners resort to coarse, heuristically-driven strategies which often fail to generalize to new and varied surroundings. Further, many of these approaches are not designed to contend with partial-observability. We posit that such uncertainty in environment geometry can, in fact, help \textit{drive} the sampling process in generating feasible, and probabilistically-safe planning graphs. We propose a method for Probabilistic Roadmaps which relies on particle-based Variational Inference to efficiently cover the posterior distribution over feasible regions in configuration space. Our approach, Stein Variational Probabilistic Roadmap (SV-PRM), results in sample-efficient generation of planning-graphs and large improvements over traditional sampling approaches. We demonstrate the approach on a variety of challenging planning problems, including real-world probabilistic occupancy maps and high-dof manipulation problems common in robotics.

Guided Incremental Local Densification for Accelerated Sampling-based Motion Planning

Sampling-based motion planners rely on incremental densification to discover progressively shorter paths. After computing feasible path $\xi$ between start $x_s$ and goal $x_t$, the Informed Set (IS) prunes the configuration space $\mathcal{C}$ by conservatively eliminating points that cannot yield shorter paths. Densification via sampling from this Informed Set retains asymptotic optimality of sampling from the entire configuration space. For path length $c(\xi)$ and Euclidean heuristic $h$, $IS = \{ x | x \in \mathcal{C}, h(x_s, x) + h(x, x_t) \leq c(\xi) \}$. Relying on the heuristic can render the IS especially conservative in high dimensions or complex environments. Furthermore, the IS only shrinks when shorter paths are discovered. Thus, the computational effort from each iteration of densification and planning is wasted if it fails to yield a shorter path, despite improving the cost-to-come for vertices in the search tree. Our key insight is that even in such a failure, shorter paths to vertices in the search tree (rather than just the goal) can immediately improve the planner's sampling strategy. Guided Incremental Local Densification (GuILD) leverages this information to sample from Local Subsets of the IS. We show that GuILD significantly outperforms uniform sampling of the Informed Set in simulated $\mathbb{R}^2$, $SE(2)$ environments and manipulation tasks in $\mathbb{R}^7$.

Posterior Sampling for Anytime Motion Planning on Graphs with Expensive-to-Evaluate Edges

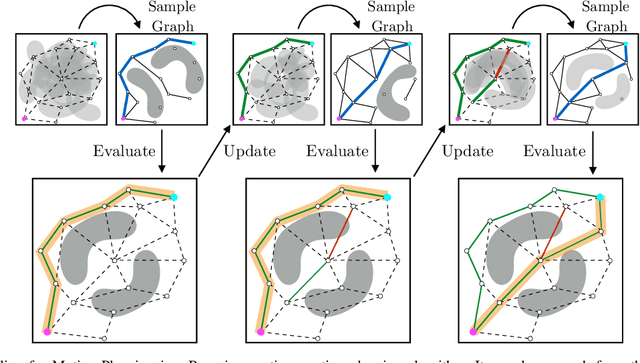
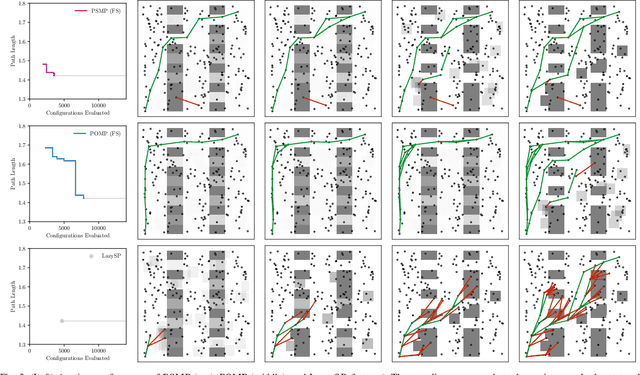
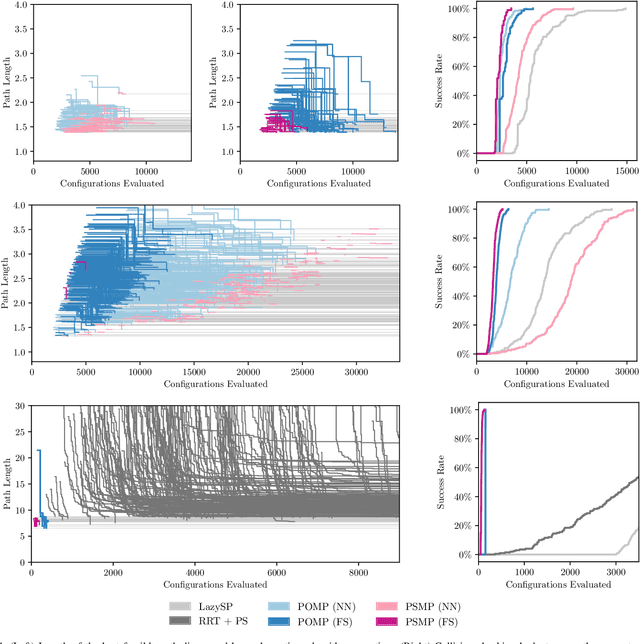
Collision checking is a computational bottleneck in motion planning, requiring lazy algorithms that explicitly reason about when to perform this computation. Optimism in the face of collision uncertainty minimizes the number of checks before finding the shortest path. However, this may take a prohibitively long time to compute, with no other feasible paths discovered during this period. For many real-time applications, we instead demand strong anytime performance, defined as minimizing the cumulative lengths of the feasible paths yielded over time. We introduce Posterior Sampling for Motion Planning (PSMP), an anytime lazy motion planning algorithm that leverages learned posteriors on edge collisions to quickly discover an initial feasible path and progressively yield shorter paths. PSMP obtains an expected regret bound of $\tilde{O}(\sqrt{\mathcal{S} \mathcal{A} T})$ and outperforms comparative baselines on a set of 2D and 7D planning problems.

Bayesian Residual Policy Optimization: Scalable Bayesian Reinforcement Learning with Clairvoyant Experts

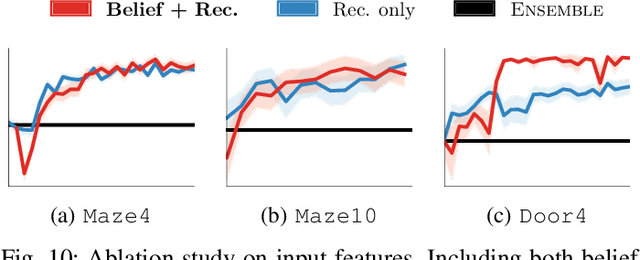
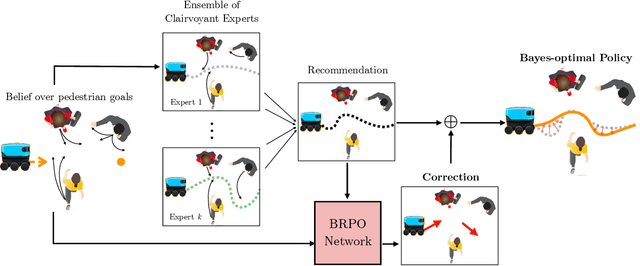
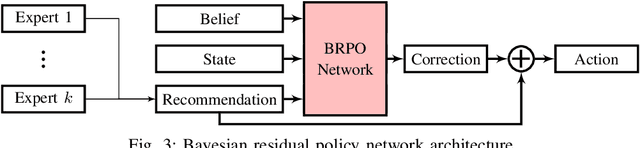
Informed and robust decision making in the face of uncertainty is critical for robots that perform physical tasks alongside people. We formulate this as Bayesian Reinforcement Learning over latent Markov Decision Processes (MDPs). While Bayes-optimality is theoretically the gold standard, existing algorithms do not scale well to continuous state and action spaces. Our proposal builds on the following insight: in the absence of uncertainty, each latent MDP is easier to solve. We first obtain an ensemble of experts, one for each latent MDP, and fuse their advice to compute a baseline policy. Next, we train a Bayesian residual policy to improve upon the ensemble's recommendation and learn to reduce uncertainty. Our algorithm, Bayesian Residual Policy Optimization (BRPO), imports the scalability of policy gradient methods and task-specific expert skills. BRPO significantly improves the ensemble of experts and drastically outperforms existing adaptive RL methods.

Sample-Efficient Learning of Nonprehensile Manipulation Policies via Physics-Based Informed State Distributions

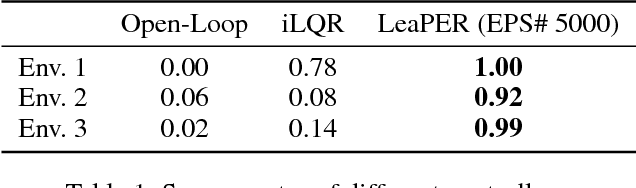
This paper proposes a sample-efficient yet simple approach to learning closed-loop policies for nonprehensile manipulation. Although reinforcement learning (RL) can learn closed-loop policies without requiring access to underlying physics models, it suffers from poor sample complexity on challenging tasks. To overcome this problem, we leverage rearrangement planning to provide an informative physics-based prior on the environment's optimal state-visitation distribution. Specifically, we present a new technique, Learning with Planned Episodic Resets (LeaPER), that resets the environment's state to one informed by the prior during the learning phase. We experimentally show that LeaPER significantly outperforms traditional RL approaches by a factor of up to 5X on simulated rearrangement. Further, we relax dynamics from quasi-static to welded contacts to illustrate that LeaPER is robust to the use of simpler physics models. Finally, LeaPER's closed-loop policies significantly improve task success rates relative to both open-loop controls with a planned path or simple feedback controllers that track open-loop trajectories. We demonstrate the performance and behavior of LeaPER on a physical 7-DOF manipulator in https://youtu.be/feS-zFq6J1c.

Bayes-CPACE: PAC Optimal Exploration in Continuous Space Bayes-Adaptive Markov Decision Processes

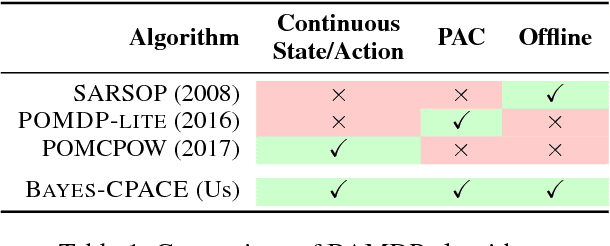
We present the first PAC optimal algorithm for Bayes-Adaptive Markov Decision Processes (BAMDPs) in continuous state and action spaces, to the best of our knowledge. The BAMDP framework elegantly addresses model uncertainty by incorporating Bayesian belief updates into long-term expected return. However, computing an exact optimal Bayesian policy is intractable. Our key insight is to compute a near-optimal value function by covering the continuous state-belief-action space with a finite set of representative samples and exploiting the Lipschitz continuity of the value function. We prove the near-optimality of our algorithm and analyze a number of schemes that boost the algorithm's efficiency. Finally, we empirically validate our approach on a number of discrete and continuous BAMDPs and show that the learned policy has consistently competitive performance against baseline approaches.

Bayesian Policy Optimization for Model Uncertainty

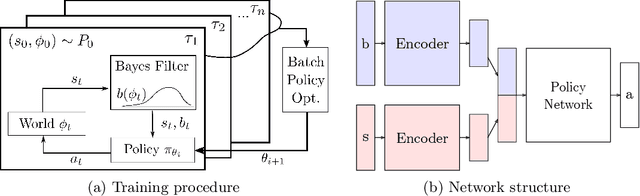
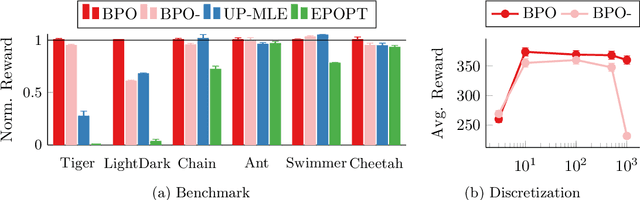
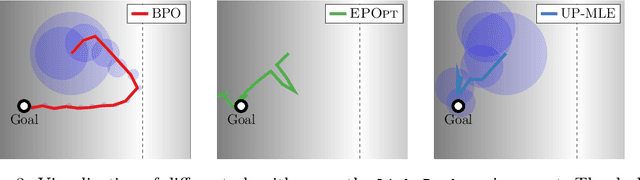
Addressing uncertainty is critical for autonomous systems to robustly adapt to the real world. We formulate the problem of model uncertainty as a continuous Bayes-Adaptive Markov Decision Process (BAMDP), where an agent maintains a posterior distribution over the latent model parameters given a history of observations and maximizes its expected long-term reward with respect to this belief distribution. Our algorithm, Bayesian Policy Optimization, builds on recent policy optimization algorithms to learn a universal policy that navigates the exploration-exploitation trade-off to maximize the Bayesian value function. To address challenges from discretizing the continuous latent parameter space, we propose a policy network architecture that independently encodes the belief distribution from the observable state. Our method significantly outperforms algorithms that address model uncertainty without explicitly reasoning about belief distributions, and is competitive with state-of-the-art Partially Observable Markov Decision Process solvers.

Efficient motion planning for problems lacking optimal substructure

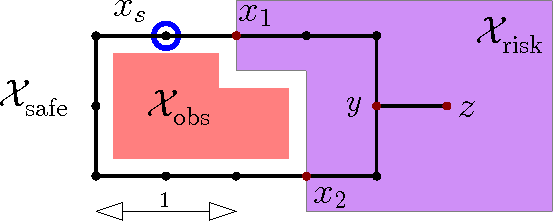
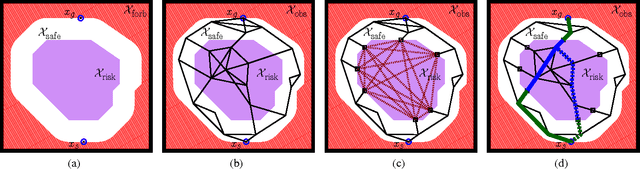
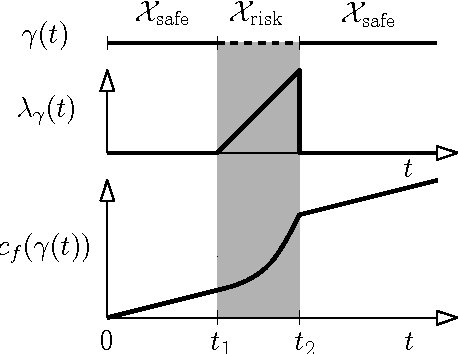
We consider the motion-planning problem of planning a collision-free path of a robot in the presence of risk zones. The robot is allowed to travel in these zones but is penalized in a super-linear fashion for consecutive accumulative time spent there. We suggest a natural cost function that balances path length and risk-exposure time. Specifically, we consider the discrete setting where we are given a graph, or a roadmap, and we wish to compute the minimal-cost path under this cost function. Interestingly, paths defined using our cost function do not have an optimal substructure. Namely, subpaths of an optimal path are not necessarily optimal. Thus, the Bellman condition is not satisfied and standard graph-search algorithms such as Dijkstra cannot be used. We present a path-finding algorithm, which can be seen as a natural generalization of Dijkstra's algorithm. Our algorithm runs in $O\left((n_B\cdot n) \log( n_B\cdot n) + n_B\cdot m\right)$ time, where~$n$ and $m$ are the number of vertices and edges of the graph, respectively, and $n_B$ is the number of intersections between edges and the boundary of the risk zone. We present simulations on robotic platforms demonstrating both the natural paths produced by our cost function and the computational efficiency of our algorithm.