Fast and Feature-Complete Differentiable Physics for Articulated Rigid Bodies with Contact

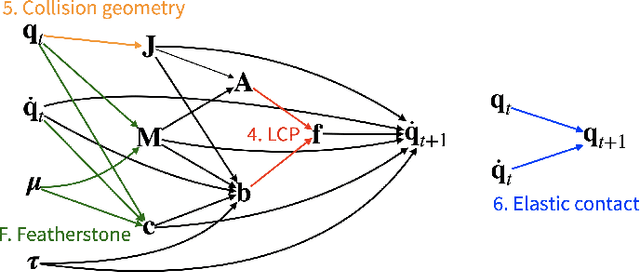
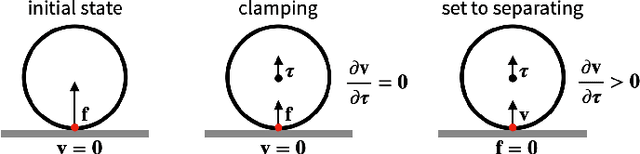
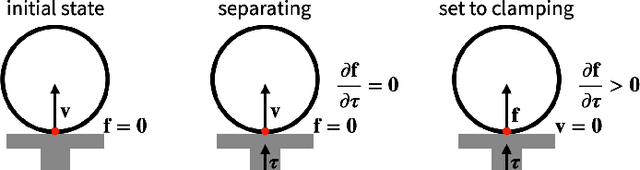
We present a fast and feature-complete differentiable physics engine that supports Lagrangian dynamics and hard contact constraints for articulated rigid body simulation. Our differentiable physics engine offers a complete set of features that are typically only available in non-differentiable physics simulators commonly used by robotics applications. We solve contact constraints precisely using linear complementarity problems (LCPs). We present efficient and novel analytical gradients through the LCP formulation of inelastic contact that exploit the sparsity of the LCP solution. We support complex contact geometry, and gradients approximating continuous-time elastic collision. We also introduce a novel method to compute complementarity-aware gradients that help downstream optimization tasks avoid stalling in saddle points. We show that an implementation of this combination in an existing physics engine (DART) is capable of a 45x single-core speedup over finite-differencing in computing analytical Jacobians for a single timestep, while preserving all the expressiveness of original DART.