Motion Manifold Flow Primitives for Language-Guided Trajectory Generation

Developing text-based robot trajectory generation models is made particularly difficult by the small dataset size, high dimensionality of the trajectory space, and the inherent complexity of the text-conditional motion distribution. Recent manifold learning-based methods have partially addressed the dimensionality and dataset size issues, but struggle with the complex text-conditional distribution. In this paper we propose a text-based trajectory generation model that attempts to address all three challenges while relying on only a handful of demonstration trajectory data. Our key idea is to leverage recent flow-based models capable of capturing complex conditional distributions, not directly in the high-dimensional trajectory space, but rather in the low-dimensional latent coordinate space of the motion manifold, with deliberately designed regularization terms to ensure smoothness of motions and robustness to text variations. We show that our {\it Motion Manifold Flow Primitive (MMFP)} framework can accurately generate qualitatively distinct motions for a wide range of text inputs, significantly outperforming existing methods.

Maximum Entropy Inverse Reinforcement Learning of Diffusion Models with Energy-Based Models

We present a maximum entropy inverse reinforcement learning (IRL) approach for improving the sample quality of diffusion generative models, especially when the number of generation time steps is small. Similar to how IRL trains a policy based on the reward function learned from expert demonstrations, we train (or fine-tune) a diffusion model using the log probability density estimated from training data. Since we employ an energy-based model (EBM) to represent the log density, our approach boils down to the joint training of a diffusion model and an EBM. Our IRL formulation, named Diffusion by Maximum Entropy IRL (DxMI), is a minimax problem that reaches equilibrium when both models converge to the data distribution. The entropy maximization plays a key role in DxMI, facilitating the exploration of the diffusion model and ensuring the convergence of the EBM. We also propose Diffusion by Dynamic Programming (DxDP), a novel reinforcement learning algorithm for diffusion models, as a subroutine in DxMI. DxDP makes the diffusion model update in DxMI efficient by transforming the original problem into an optimal control formulation where value functions replace back-propagation in time. Our empirical studies show that diffusion models fine-tuned using DxMI can generate high-quality samples in as few as 4 and 10 steps. Additionally, DxMI enables the training of an EBM without MCMC, stabilizing EBM training dynamics and enhancing anomaly detection performance.

Generalized Contrastive Divergence: Joint Training of Energy-Based Model and Diffusion Model through Inverse Reinforcement Learning

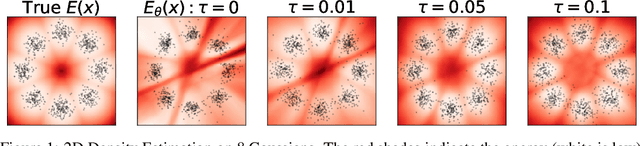
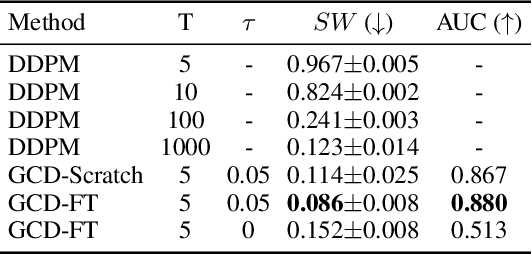
We present Generalized Contrastive Divergence (GCD), a novel objective function for training an energy-based model (EBM) and a sampler simultaneously. GCD generalizes Contrastive Divergence (Hinton, 2002), a celebrated algorithm for training EBM, by replacing Markov Chain Monte Carlo (MCMC) distribution with a trainable sampler, such as a diffusion model. In GCD, the joint training of EBM and a diffusion model is formulated as a minimax problem, which reaches an equilibrium when both models converge to the data distribution. The minimax learning with GCD bears interesting equivalence to inverse reinforcement learning, where the energy corresponds to a negative reward, the diffusion model is a policy, and the real data is expert demonstrations. We present preliminary yet promising results showing that joint training is beneficial for both EBM and a diffusion model. GCD enables EBM training without MCMC while improving the sample quality of a diffusion model.

Variational Weighting for Kernel Density Ratios

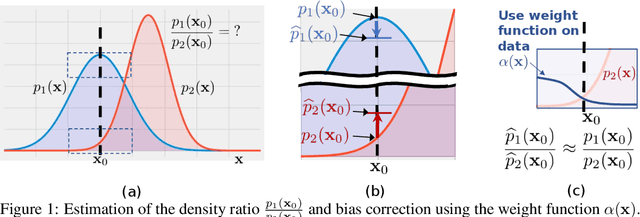
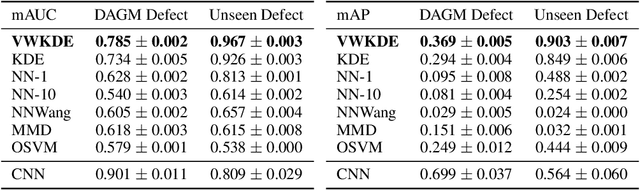
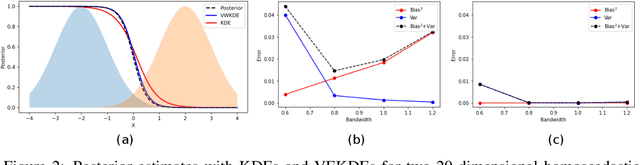
Kernel density estimation (KDE) is integral to a range of generative and discriminative tasks in machine learning. Drawing upon tools from the multidimensional calculus of variations, we derive an optimal weight function that reduces bias in standard kernel density estimates for density ratios, leading to improved estimates of prediction posteriors and information-theoretic measures. In the process, we shed light on some fundamental aspects of density estimation, particularly from the perspective of algorithms that employ KDEs as their main building blocks.

Energy-Based Models for Anomaly Detection: A Manifold Diffusion Recovery Approach

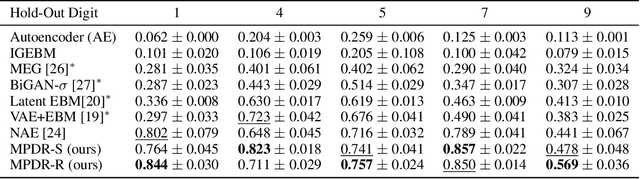
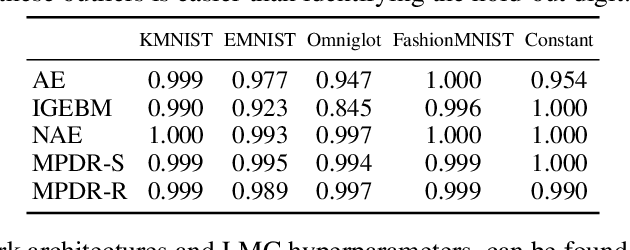
We present a new method of training energy-based models (EBMs) for anomaly detection that leverages low-dimensional structures within data. The proposed algorithm, Manifold Projection-Diffusion Recovery (MPDR), first perturbs a data point along a low-dimensional manifold that approximates the training dataset. Then, EBM is trained to maximize the probability of recovering the original data. The training involves the generation of negative samples via MCMC, as in conventional EBM training, but from a different distribution concentrated near the manifold. The resulting near-manifold negative samples are highly informative, reflecting relevant modes of variation in data. An energy function of MPDR effectively learns accurate boundaries of the training data distribution and excels at detecting out-of-distribution samples. Experimental results show that MPDR exhibits strong performance across various anomaly detection tasks involving diverse data types, such as images, vectors, and acoustic signals.

A Linear-Time Variational Integrator for Multibody Systems

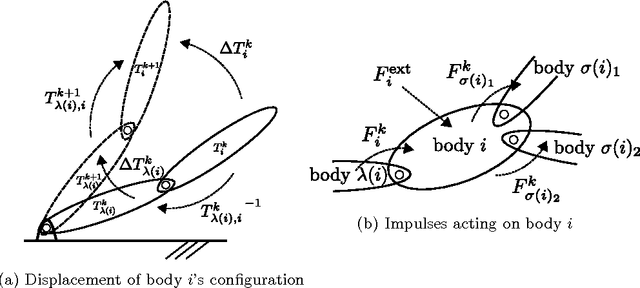
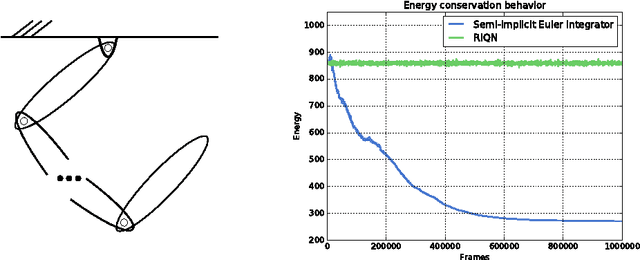
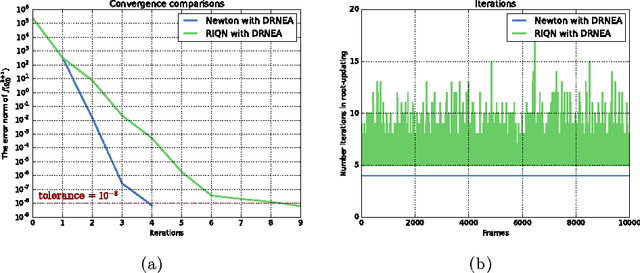
We present an efficient variational integrator for multibody systems. Variational integrators reformulate the equations of motion for multibody systems as discrete Euler-Lagrange (DEL) equations, transforming forward integration into a root-finding problem for the DEL equations. Variational integrators have been shown to be more robust and accurate in preserving fundamental properties of systems, such as momentum and energy, than many frequently used numerical integrators. However, state-of-the-art algorithms suffer from $O(n^3)$ complexity, which is prohibitive for articulated multibody systems with a large number of degrees of freedom, $n$, in generalized coordinates. Our key contribution is to derive a recursive algorithm that evaluates DEL equations in $O(n)$, which scales up well for complex multibody systems such as humanoid robots. Inspired by recursive Newton-Euler algorithm, our key insight is to formulate DEL equation individually for each body rather than for the entire system. Furthermore, we introduce a new quasi-Newton method that exploits the impulse-based dynamics algorithm, which is also $O(n)$, to avoid the expensive Jacobian inversion in solving DEL equations. We demonstrate scalability and efficiency, as well as extensibility to holonomic constraints through several case studies.