Value Gradient Sampler: Sampling as Sequential Decision Making

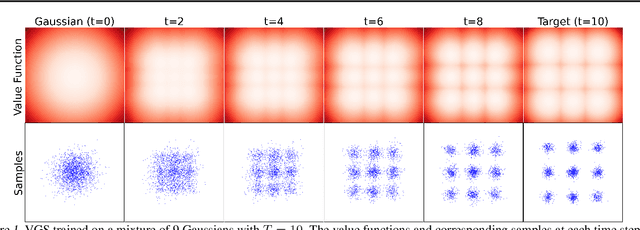
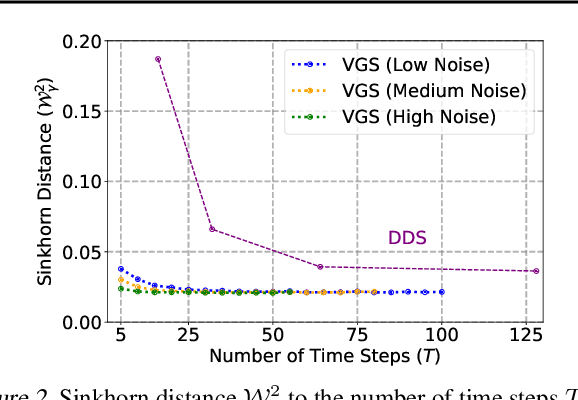
We propose the Value Gradient Sampler (VGS), a trainable sampler based on the interpretation of sampling as discrete-time sequential decision-making. VGS generates samples from a given unnormalized density (i.e., energy) by drifting and diffusing randomly initialized particles. In VGS, finding the optimal drift is equivalent to solving an optimal control problem where the cost is the upper bound of the KL divergence between the target density and the samples. We employ value-based dynamic programming to solve this optimal control problem, which gives the gradient of the value function as the optimal drift vector. The connection to sequential decision making allows VGS to leverage extensively studied techniques in reinforcement learning, making VGS a fast, adaptive, and accurate sampler that achieves competitive results in various sampling benchmarks. Furthermore, VGS can replace MCMC in contrastive divergence training of energy-based models. We demonstrate the effectiveness of VGS in training accurate energy-based models in industrial anomaly detection applications.

Maximum Entropy Inverse Reinforcement Learning of Diffusion Models with Energy-Based Models

We present a maximum entropy inverse reinforcement learning (IRL) approach for improving the sample quality of diffusion generative models, especially when the number of generation time steps is small. Similar to how IRL trains a policy based on the reward function learned from expert demonstrations, we train (or fine-tune) a diffusion model using the log probability density estimated from training data. Since we employ an energy-based model (EBM) to represent the log density, our approach boils down to the joint training of a diffusion model and an EBM. Our IRL formulation, named Diffusion by Maximum Entropy IRL (DxMI), is a minimax problem that reaches equilibrium when both models converge to the data distribution. The entropy maximization plays a key role in DxMI, facilitating the exploration of the diffusion model and ensuring the convergence of the EBM. We also propose Diffusion by Dynamic Programming (DxDP), a novel reinforcement learning algorithm for diffusion models, as a subroutine in DxMI. DxDP makes the diffusion model update in DxMI efficient by transforming the original problem into an optimal control formulation where value functions replace back-propagation in time. Our empirical studies show that diffusion models fine-tuned using DxMI can generate high-quality samples in as few as 4 and 10 steps. Additionally, DxMI enables the training of an EBM without MCMC, stabilizing EBM training dynamics and enhancing anomaly detection performance.

Generalized Contrastive Divergence: Joint Training of Energy-Based Model and Diffusion Model through Inverse Reinforcement Learning

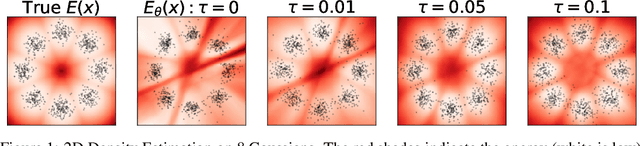
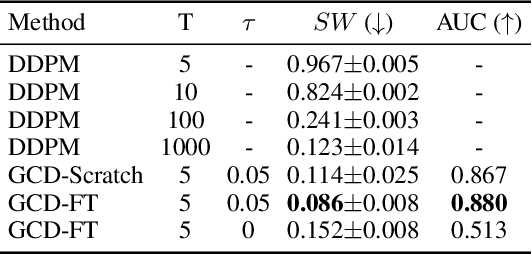
We present Generalized Contrastive Divergence (GCD), a novel objective function for training an energy-based model (EBM) and a sampler simultaneously. GCD generalizes Contrastive Divergence (Hinton, 2002), a celebrated algorithm for training EBM, by replacing Markov Chain Monte Carlo (MCMC) distribution with a trainable sampler, such as a diffusion model. In GCD, the joint training of EBM and a diffusion model is formulated as a minimax problem, which reaches an equilibrium when both models converge to the data distribution. The minimax learning with GCD bears interesting equivalence to inverse reinforcement learning, where the energy corresponds to a negative reward, the diffusion model is a policy, and the real data is expert demonstrations. We present preliminary yet promising results showing that joint training is beneficial for both EBM and a diffusion model. GCD enables EBM training without MCMC while improving the sample quality of a diffusion model.