Frank Chongwoo Park
Value Gradient Sampler: Sampling as Sequential Decision Making
Feb 18, 2025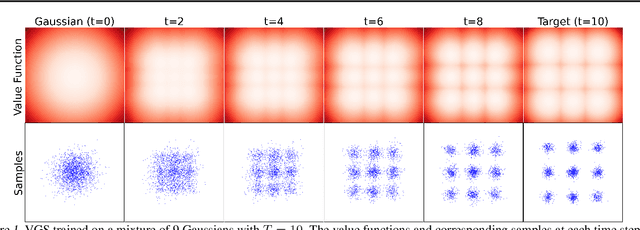

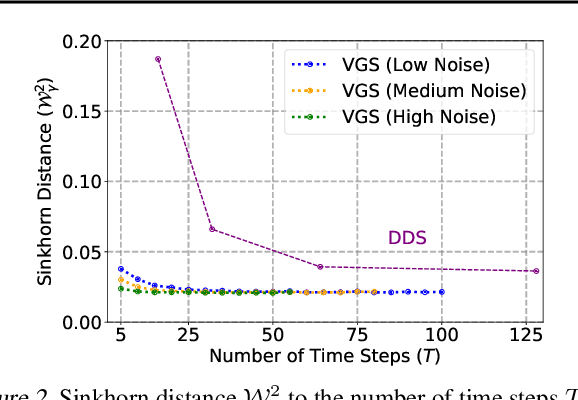

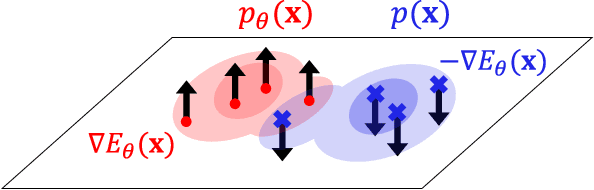
Abstract:We propose the Value Gradient Sampler (VGS), a trainable sampler based on the interpretation of sampling as discrete-time sequential decision-making. VGS generates samples from a given unnormalized density (i.e., energy) by drifting and diffusing randomly initialized particles. In VGS, finding the optimal drift is equivalent to solving an optimal control problem where the cost is the upper bound of the KL divergence between the target density and the samples. We employ value-based dynamic programming to solve this optimal control problem, which gives the gradient of the value function as the optimal drift vector. The connection to sequential decision making allows VGS to leverage extensively studied techniques in reinforcement learning, making VGS a fast, adaptive, and accurate sampler that achieves competitive results in various sampling benchmarks. Furthermore, VGS can replace MCMC in contrastive divergence training of energy-based models. We demonstrate the effectiveness of VGS in training accurate energy-based models in industrial anomaly detection applications.
On Explicit Curvature Regularization in Deep Generative Models
Sep 19, 2023Abstract:We propose a family of curvature-based regularization terms for deep generative model learning. Explicit coordinate-invariant formulas for both intrinsic and extrinsic curvature measures are derived for the case of arbitrary data manifolds embedded in higher-dimensional Euclidean space. Because computing the curvature is a highly computation-intensive process involving the evaluation of second-order derivatives, efficient formulas are derived for approximately evaluating intrinsic and extrinsic curvatures. Comparative studies are conducted that compare the relative efficacy of intrinsic versus extrinsic curvature-based regularization measures, as well as performance comparisons against existing autoencoder training methods. Experiments involving noisy motion capture data confirm that curvature-based methods outperform existing autoencoder regularization methods, with intrinsic curvature measures slightly more effective than extrinsic curvature measures.
Evaluating Out-of-Distribution Detectors Through Adversarial Generation of Outliers
Aug 20, 2022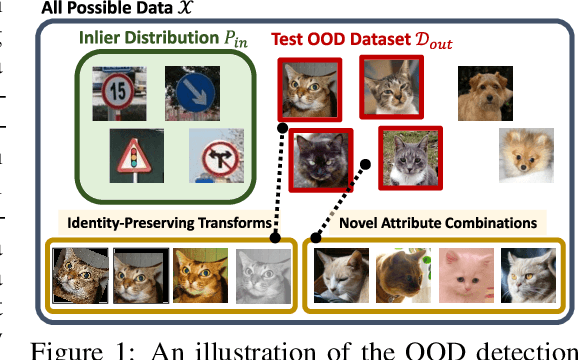
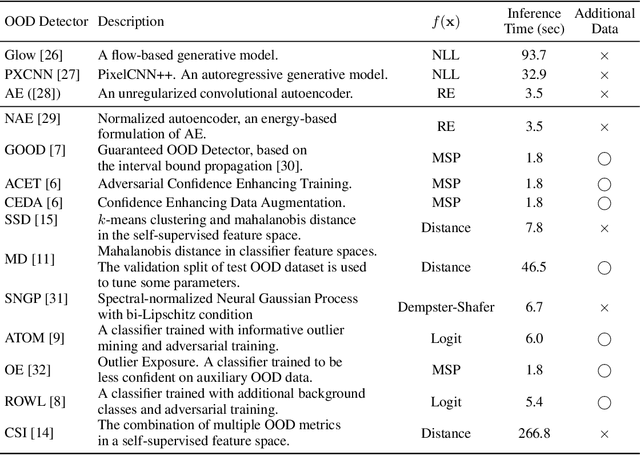
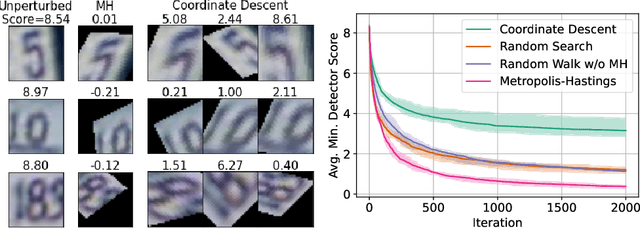
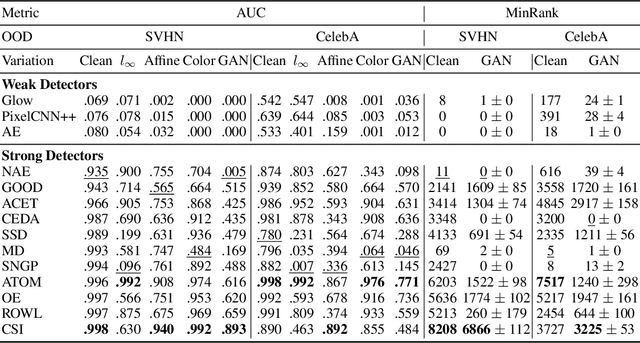
Abstract:A reliable evaluation method is essential for building a robust out-of-distribution (OOD) detector. Current robustness evaluation protocols for OOD detectors rely on injecting perturbations to outlier data. However, the perturbations are unlikely to occur naturally or not relevant to the content of data, providing a limited assessment of robustness. In this paper, we propose Evaluation-via-Generation for OOD detectors (EvG), a new protocol for investigating the robustness of OOD detectors under more realistic modes of variation in outliers. EvG utilizes a generative model to synthesize plausible outliers, and employs MCMC sampling to find outliers misclassified as in-distribution with the highest confidence by a detector. We perform a comprehensive benchmark comparison of the performance of state-of-the-art OOD detectors using EvG, uncovering previously overlooked weaknesses.
Autoencoding Under Normalization Constraints
May 12, 2021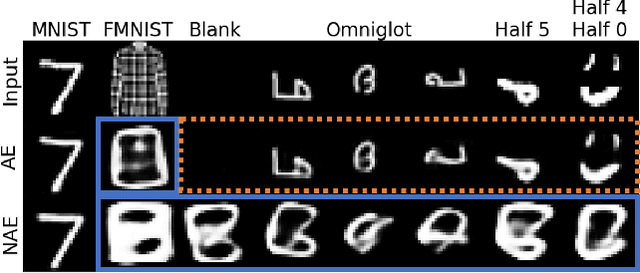


Abstract:Likelihood is a standard estimate for outlier detection. The specific role of the normalization constraint is to ensure that the out-of-distribution (OOD) regime has a small likelihood when samples are learned using maximum likelihood. Because autoencoders do not possess such a process of normalization, they often fail to recognize outliers even when they are obviously OOD. We propose the Normalized Autoencoder (NAE), a normalized probabilistic model constructed from an autoencoder. The probability density of NAE is defined using the reconstruction error of an autoencoder, which is differently defined in the conventional energy-based model. In our model, normalization is enforced by suppressing the reconstruction of negative samples, significantly improving the outlier detection performance. Our experimental results confirm the efficacy of NAE, both in detecting outliers and in generating in-distribution samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge