High-Bandwidth Tactile-Reactive Control for Grasp Adjustment

Vision-only grasping systems are fundamentally constrained by calibration errors, sensor noise, and grasp pose prediction inaccuracies, leading to unavoidable contact uncertainty in the final stage of grasping. High-bandwidth tactile feedback, when paired with a well-designed tactile-reactive controller, can significantly improve robustness in the presence of perception errors. This paper contributes to controller design by proposing a purely tactile-feedback grasp-adjustment algorithm. The proposed controller requires neither prior knowledge of the object's geometry nor an accurate grasp pose, and is capable of refining a grasp even when starting from a crude, imprecise initial configuration and uncertain contact points. Through simulation studies and real-world experiments on a 15-DoF arm-hand system (featuring an 8-DoF hand) equipped with fingertip tactile sensors operating at 200 Hz, we demonstrate that our tactile-reactive grasping framework effectively improves grasp stability.

Trajectory Manifold Optimization for Fast and Adaptive Kinodynamic Motion Planning

Fast kinodynamic motion planning is crucial for systems to effectively adapt to dynamically changing environments. Despite some efforts, existing approaches still struggle with rapid planning in high-dimensional, complex problems. Not surprisingly, the primary challenge arises from the high-dimensionality of the search space, specifically the trajectory space. We address this issue with a two-step method: initially, we identify a lower-dimensional trajectory manifold {\it offline}, comprising diverse trajectories specifically relevant to the task at hand while meeting kinodynamic constraints. Subsequently, we search for solutions within this manifold {\it online}, significantly enhancing the planning speed. To encode and generate a manifold of continuous-time, differentiable trajectories, we propose a novel neural network model, {\it Differentiable Motion Manifold Primitives (DMMP)}, along with a practical training strategy. Experiments with a 7-DoF robot arm tasked with dynamic throwing to arbitrary target positions demonstrate that our method surpasses existing approaches in planning speed, task success, and constraint satisfaction.

Motion Manifold Flow Primitives for Language-Guided Trajectory Generation

Developing text-based robot trajectory generation models is made particularly difficult by the small dataset size, high dimensionality of the trajectory space, and the inherent complexity of the text-conditional motion distribution. Recent manifold learning-based methods have partially addressed the dimensionality and dataset size issues, but struggle with the complex text-conditional distribution. In this paper we propose a text-based trajectory generation model that attempts to address all three challenges while relying on only a handful of demonstration trajectory data. Our key idea is to leverage recent flow-based models capable of capturing complex conditional distributions, not directly in the high-dimensional trajectory space, but rather in the low-dimensional latent coordinate space of the motion manifold, with deliberately designed regularization terms to ensure smoothness of motions and robustness to text variations. We show that our {\it Motion Manifold Flow Primitive (MMFP)} framework can accurately generate qualitatively distinct motions for a wide range of text inputs, significantly outperforming existing methods.

Isometric Motion Manifold Primitives

The Motion Manifold Primitive (MMP) produces, for a given task, a continuous manifold of trajectories each of which can successfully complete the task. It consists of the decoder function that parametrizes the manifold and the probability density in the latent coordinate space. In this paper, we first show that the MMP performance can significantly degrade due to the geometric distortion in the latent space -- by distortion, we mean that similar motions are not located nearby in the latent space. We then propose {\it Isometric Motion Manifold Primitives (IMMP)} whose latent coordinate space preserves the geometry of the manifold. For this purpose, we formulate and use a Riemannian metric for the motion space (i.e., parametric curve space), which we call a {\it CurveGeom Riemannian metric}. Experiments with planar obstacle-avoiding motions and pushing manipulation tasks show that IMMP significantly outperforms existing MMP methods. Code is available at https://github.com/Gabe-YHLee/IMMP-public.

A Geometric Perspective on Autoencoders

This paper presents the geometric aspect of the autoencoder framework, which, despite its importance, has been relatively less recognized. Given a set of high-dimensional data points that approximately lie on some lower-dimensional manifold, an autoencoder learns the \textit{manifold} and its \textit{coordinate chart}, simultaneously. This geometric perspective naturally raises inquiries like "Does a finite set of data points correspond to a single manifold?" or "Is there only one coordinate chart that can represent the manifold?". The responses to these questions are negative, implying that there are multiple solution autoencoders given a dataset. Consequently, they sometimes produce incorrect manifolds with severely distorted latent space representations. In this paper, we introduce recent geometric approaches that address these issues.

On Explicit Curvature Regularization in Deep Generative Models

We propose a family of curvature-based regularization terms for deep generative model learning. Explicit coordinate-invariant formulas for both intrinsic and extrinsic curvature measures are derived for the case of arbitrary data manifolds embedded in higher-dimensional Euclidean space. Because computing the curvature is a highly computation-intensive process involving the evaluation of second-order derivatives, efficient formulas are derived for approximately evaluating intrinsic and extrinsic curvatures. Comparative studies are conducted that compare the relative efficacy of intrinsic versus extrinsic curvature-based regularization measures, as well as performance comparisons against existing autoencoder training methods. Experiments involving noisy motion capture data confirm that curvature-based methods outperform existing autoencoder regularization methods, with intrinsic curvature measures slightly more effective than extrinsic curvature measures.

Evaluating Out-of-Distribution Detectors Through Adversarial Generation of Outliers

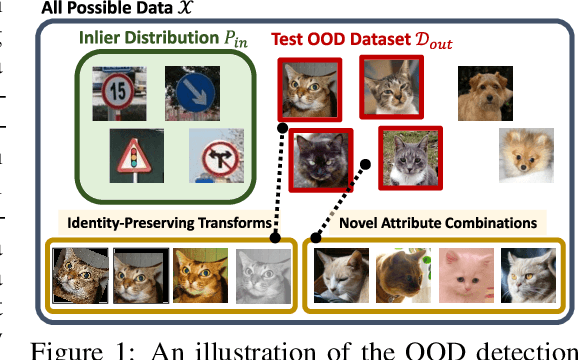
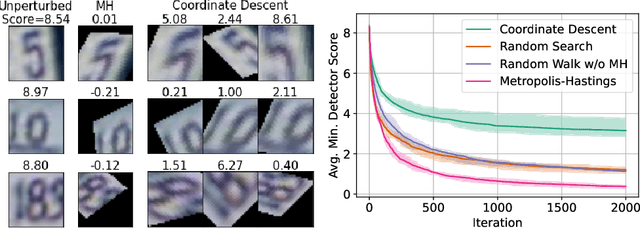
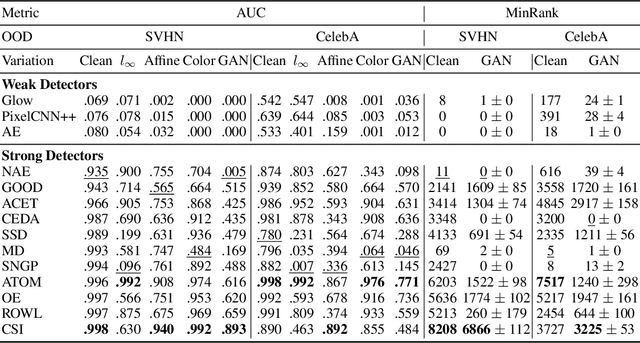
A reliable evaluation method is essential for building a robust out-of-distribution (OOD) detector. Current robustness evaluation protocols for OOD detectors rely on injecting perturbations to outlier data. However, the perturbations are unlikely to occur naturally or not relevant to the content of data, providing a limited assessment of robustness. In this paper, we propose Evaluation-via-Generation for OOD detectors (EvG), a new protocol for investigating the robustness of OOD detectors under more realistic modes of variation in outliers. EvG utilizes a generative model to synthesize plausible outliers, and employs MCMC sampling to find outliers misclassified as in-distribution with the highest confidence by a detector. We perform a comprehensive benchmark comparison of the performance of state-of-the-art OOD detectors using EvG, uncovering previously overlooked weaknesses.