Overcoming Fake Solutions in Semi-Dual Neural Optimal Transport: A Smoothing Approach for Learning the Optimal Transport Plan

We address the convergence problem in learning the Optimal Transport (OT) map, where the OT Map refers to a map from one distribution to another while minimizing the transport cost. Semi-dual Neural OT, a widely used approach for learning OT Maps with neural networks, often generates fake solutions that fail to transfer one distribution to another accurately. We identify a sufficient condition under which the max-min solution of Semi-dual Neural OT recovers the true OT Map. Moreover, to address cases when this sufficient condition is not satisfied, we propose a novel method, OTP, which learns both the OT Map and the Optimal Transport Plan, representing the optimal coupling between two distributions. Under sharp assumptions on the distributions, we prove that our model eliminates the fake solution issue and correctly solves the OT problem. Our experiments show that the OTP model recovers the optimal transport map where existing methods fail and outperforms current OT-based models in image-to-image translation tasks. Notably, the OTP model can learn stochastic transport maps when deterministic OT Maps do not exist, such as one-to-many tasks like colorization.

Memorization Capacity for Additive Fine-Tuning with Small ReLU Networks

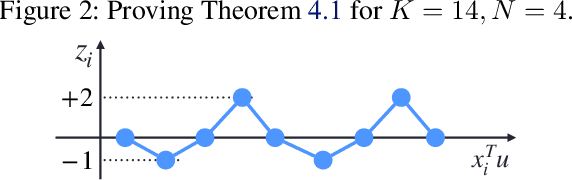
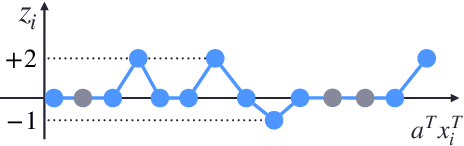
Fine-tuning large pre-trained models is a common practice in machine learning applications, yet its mathematical analysis remains largely unexplored. In this paper, we study fine-tuning through the lens of memorization capacity. Our new measure, the Fine-Tuning Capacity (FTC), is defined as the maximum number of samples a neural network can fine-tune, or equivalently, as the minimum number of neurons ($m$) needed to arbitrarily change $N$ labels among $K$ samples considered in the fine-tuning process. In essence, FTC extends the memorization capacity concept to the fine-tuning scenario. We analyze FTC for the additive fine-tuning scenario where the fine-tuned network is defined as the summation of the frozen pre-trained network $f$ and a neural network $g$ (with $m$ neurons) designed for fine-tuning. When $g$ is a ReLU network with either 2 or 3 layers, we obtain tight upper and lower bounds on FTC; we show that $N$ samples can be fine-tuned with $m=\Theta(N)$ neurons for 2-layer networks, and with $m=\Theta(\sqrt{N})$ neurons for 3-layer networks, no matter how large $K$ is. Our results recover the known memorization capacity results when $N = K$ as a special case.

Maximum Entropy Inverse Reinforcement Learning of Diffusion Models with Energy-Based Models

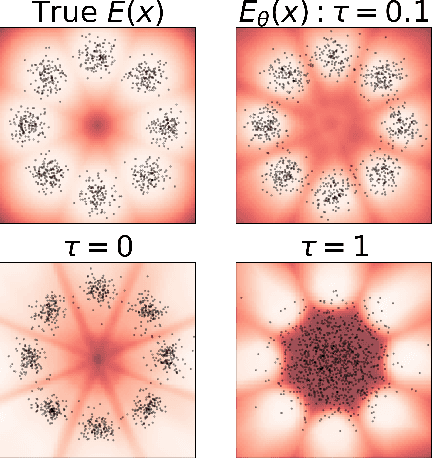
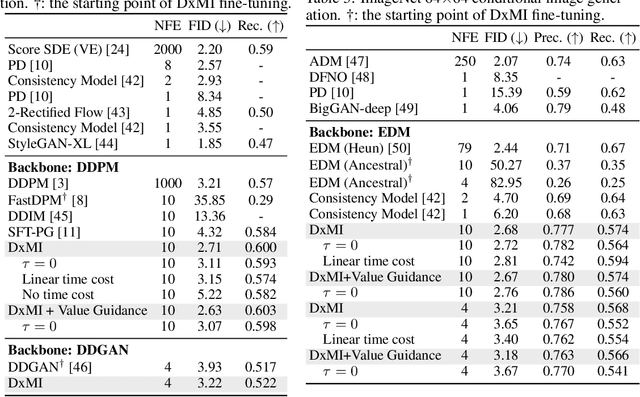
We present a maximum entropy inverse reinforcement learning (IRL) approach for improving the sample quality of diffusion generative models, especially when the number of generation time steps is small. Similar to how IRL trains a policy based on the reward function learned from expert demonstrations, we train (or fine-tune) a diffusion model using the log probability density estimated from training data. Since we employ an energy-based model (EBM) to represent the log density, our approach boils down to the joint training of a diffusion model and an EBM. Our IRL formulation, named Diffusion by Maximum Entropy IRL (DxMI), is a minimax problem that reaches equilibrium when both models converge to the data distribution. The entropy maximization plays a key role in DxMI, facilitating the exploration of the diffusion model and ensuring the convergence of the EBM. We also propose Diffusion by Dynamic Programming (DxDP), a novel reinforcement learning algorithm for diffusion models, as a subroutine in DxMI. DxDP makes the diffusion model update in DxMI efficient by transforming the original problem into an optimal control formulation where value functions replace back-propagation in time. Our empirical studies show that diffusion models fine-tuned using DxMI can generate high-quality samples in as few as 4 and 10 steps. Additionally, DxMI enables the training of an EBM without MCMC, stabilizing EBM training dynamics and enhancing anomaly detection performance.

On the Complexity of First-Order Methods in Stochastic Bilevel Optimization

We consider the problem of finding stationary points in Bilevel optimization when the lower-level problem is unconstrained and strongly convex. The problem has been extensively studied in recent years; the main technical challenge is to keep track of lower-level solutions $y^*(x)$ in response to the changes in the upper-level variables $x$. Subsequently, all existing approaches tie their analyses to a genie algorithm that knows lower-level solutions and, therefore, need not query any points far from them. We consider a dual question to such approaches: suppose we have an oracle, which we call $y^*$-aware, that returns an $O(\epsilon)$-estimate of the lower-level solution, in addition to first-order gradient estimators {\it locally unbiased} within the $\Theta(\epsilon)$-ball around $y^*(x)$. We study the complexity of finding stationary points with such an $y^*$-aware oracle: we propose a simple first-order method that converges to an $\epsilon$ stationary point using $O(\epsilon^{-6}), O(\epsilon^{-4})$ access to first-order $y^*$-aware oracles. Our upper bounds also apply to standard unbiased first-order oracles, improving the best-known complexity of first-order methods by $O(\epsilon)$ with minimal assumptions. We then provide the matching $\Omega(\epsilon^{-6})$, $\Omega(\epsilon^{-4})$ lower bounds without and with an additional smoothness assumption on $y^*$-aware oracles, respectively. Our results imply that any approach that simulates an algorithm with an $y^*$-aware oracle must suffer the same lower bounds.

Generalized Contrastive Divergence: Joint Training of Energy-Based Model and Diffusion Model through Inverse Reinforcement Learning

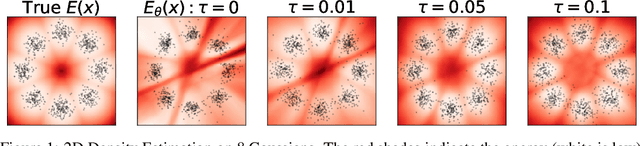
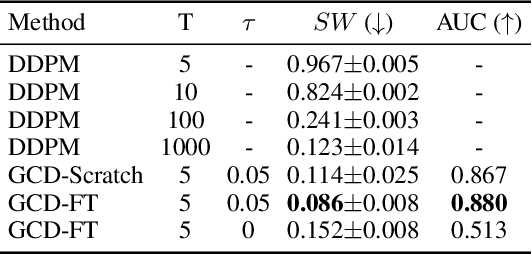
We present Generalized Contrastive Divergence (GCD), a novel objective function for training an energy-based model (EBM) and a sampler simultaneously. GCD generalizes Contrastive Divergence (Hinton, 2002), a celebrated algorithm for training EBM, by replacing Markov Chain Monte Carlo (MCMC) distribution with a trainable sampler, such as a diffusion model. In GCD, the joint training of EBM and a diffusion model is formulated as a minimax problem, which reaches an equilibrium when both models converge to the data distribution. The minimax learning with GCD bears interesting equivalence to inverse reinforcement learning, where the energy corresponds to a negative reward, the diffusion model is a policy, and the real data is expert demonstrations. We present preliminary yet promising results showing that joint training is beneficial for both EBM and a diffusion model. GCD enables EBM training without MCMC while improving the sample quality of a diffusion model.

On Penalty Methods for Nonconvex Bilevel Optimization and First-Order Stochastic Approximation

In this work, we study first-order algorithms for solving Bilevel Optimization (BO) where the objective functions are smooth but possibly nonconvex in both levels and the variables are restricted to closed convex sets. As a first step, we study the landscape of BO through the lens of penalty methods, in which the upper- and lower-level objectives are combined in a weighted sum with penalty parameter $\sigma > 0$. In particular, we establish a strong connection between the penalty function and the hyper-objective by explicitly characterizing the conditions under which the values and derivatives of the two must be $O(\sigma)$-close. A by-product of our analysis is the explicit formula for the gradient of hyper-objective when the lower-level problem has multiple solutions under minimal conditions, which could be of independent interest. Next, viewing the penalty formulation as $O(\sigma)$-approximation of the original BO, we propose first-order algorithms that find an $\epsilon$-stationary solution by optimizing the penalty formulation with $\sigma = O(\epsilon)$. When the perturbed lower-level problem uniformly satisfies the small-error proximal error-bound (EB) condition, we propose a first-order algorithm that converges to an $\epsilon$-stationary point of the penalty function, using in total $O(\epsilon^{-3})$ and $O(\epsilon^{-7})$ accesses to first-order (stochastic) gradient oracles when the oracle is deterministic and oracles are noisy, respectively. Under an additional assumption on stochastic oracles, we show that the algorithm can be implemented in a fully {\it single-loop} manner, i.e., with $O(1)$ samples per iteration, and achieves the improved oracle-complexity of $O(\epsilon^{-3})$ and $O(\epsilon^{-5})$, respectively.

Complexity of Block Coordinate Descent with Proximal Regularization and Applications to Wasserstein CP-dictionary Learning

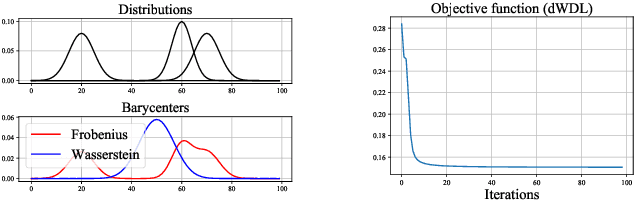
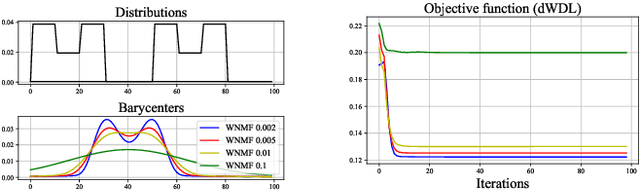
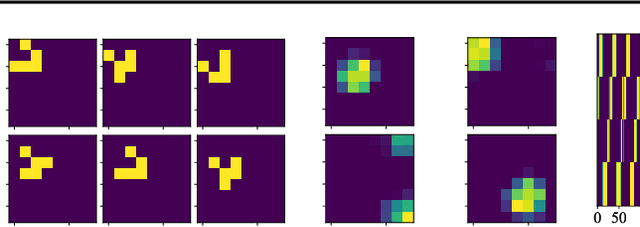
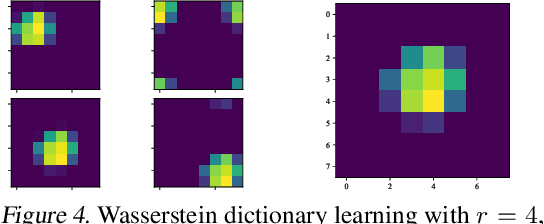
We consider the block coordinate descent methods of Gauss-Seidel type with proximal regularization (BCD-PR), which is a classical method of minimizing general nonconvex objectives under constraints that has a wide range of practical applications. We theoretically establish the worst-case complexity bound for this algorithm. Namely, we show that for general nonconvex smooth objectives with block-wise constraints, the classical BCD-PR algorithm converges to an epsilon-stationary point within O(1/epsilon) iterations. Under a mild condition, this result still holds even if the algorithm is executed inexactly in each step. As an application, we propose a provable and efficient algorithm for `Wasserstein CP-dictionary learning', which seeks a set of elementary probability distributions that can well-approximate a given set of d-dimensional joint probability distributions. Our algorithm is a version of BCD-PR that operates in the dual space, where the primal problem is regularized both entropically and proximally.

A Fully First-Order Method for Stochastic Bilevel Optimization

We consider stochastic unconstrained bilevel optimization problems when only the first-order gradient oracles are available. While numerous optimization methods have been proposed for tackling bilevel problems, existing methods either tend to require possibly expensive calculations regarding Hessians of lower-level objectives, or lack rigorous finite-time performance guarantees. In this work, we propose a Fully First-order Stochastic Approximation (F2SA) method, and study its non-asymptotic convergence properties. Specifically, we show that F2SA converges to an $\epsilon$-stationary solution of the bilevel problem after $\epsilon^{-7/2}, \epsilon^{-5/2}$, and $\epsilon^{-3/2}$ iterations (each iteration using $O(1)$ samples) when stochastic noises are in both level objectives, only in the upper-level objective, and not present (deterministic settings), respectively. We further show that if we employ momentum-assisted gradient estimators, the iteration complexities can be improved to $\epsilon^{-5/2}, \epsilon^{-4/2}$, and $\epsilon^{-3/2}$, respectively. We demonstrate even superior practical performance of the proposed method over existing second-order based approaches on MNIST data-hypercleaning experiments.

Score-based Generative Modeling Secretly Minimizes the Wasserstein Distance

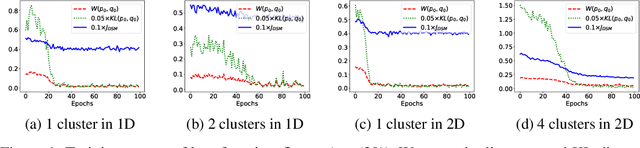
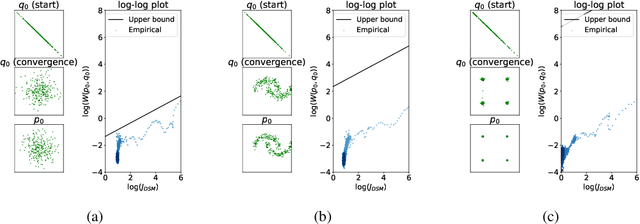
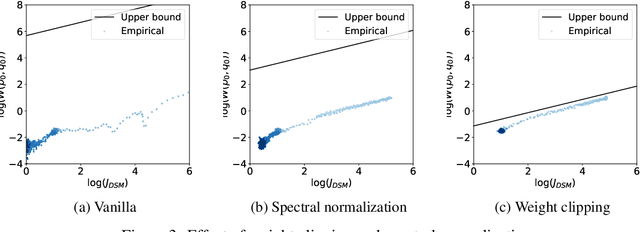
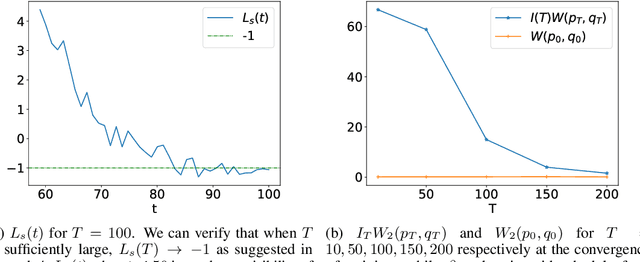
Score-based generative models are shown to achieve remarkable empirical performances in various applications such as image generation and audio synthesis. However, a theoretical understanding of score-based diffusion models is still incomplete. Recently, Song et al. showed that the training objective of score-based generative models is equivalent to minimizing the Kullback-Leibler divergence of the generated distribution from the data distribution. In this work, we show that score-based models also minimize the Wasserstein distance between them under suitable assumptions on the model. Specifically, we prove that the Wasserstein distance is upper bounded by the square root of the objective function up to multiplicative constants and a fixed constant offset. Our proof is based on a novel application of the theory of optimal transport, which can be of independent interest to the society. Our numerical experiments support our findings. By analyzing our upper bounds, we provide a few techniques to obtain tighter upper bounds.

Training Wasserstein GANs without gradient penalties

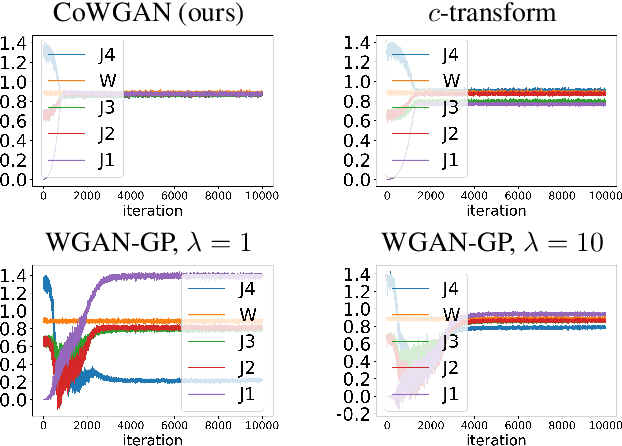
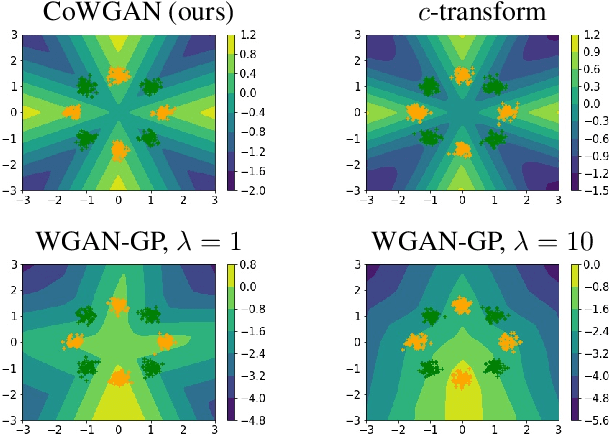
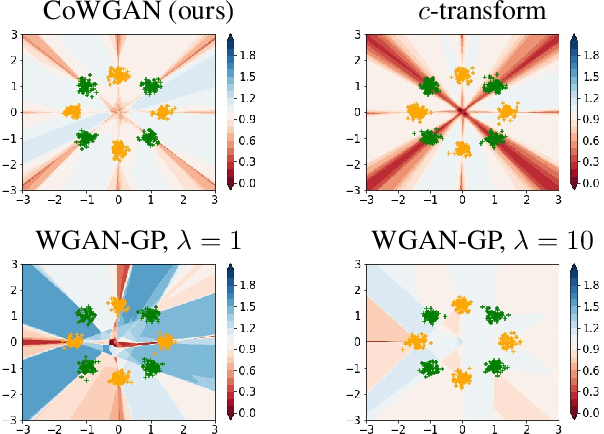
We propose a stable method to train Wasserstein generative adversarial networks. In order to enhance stability, we consider two objective functions using the $c$-transform based on Kantorovich duality which arises in the theory of optimal transport. We experimentally show that this algorithm can effectively enforce the Lipschitz constraint on the discriminator while other standard methods fail to do so. As a consequence, our method yields an accurate estimation for the optimal discriminator and also for the Wasserstein distance between the true distribution and the generated one. Our method requires no gradient penalties nor corresponding hyperparameter tuning and is computationally more efficient than other methods. At the same time, it yields competitive generators of synthetic images based on the MNIST, F-MNIST, and CIFAR-10 datasets.