A Mathematical Framework, a Taxonomy of Modeling Paradigms, and a Suite of Learning Techniques for Neural-Symbolic Systems

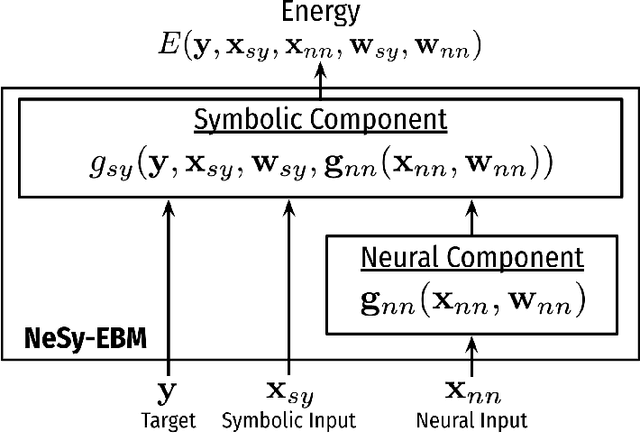
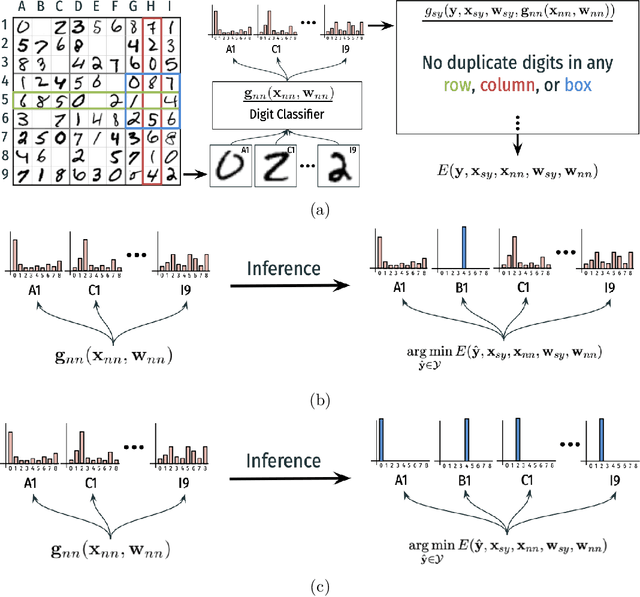
The field of Neural-Symbolic (NeSy) systems is growing rapidly. Proposed approaches show great promise in achieving symbiotic unions of neural and symbolic methods. However, each NeSy system differs in fundamental ways. There is a pressing need for a unifying theory to illuminate the commonalities and differences in approaches and enable further progress. In this paper, we introduce Neural-Symbolic Energy-Based Models (NeSy-EBMs), a unifying mathematical framework for discriminative and generative modeling with probabilistic and non-probabilistic NeSy approaches. We utilize NeSy-EBMs to develop a taxonomy of modeling paradigms focusing on a system's neural-symbolic interface and reasoning capabilities. Additionally, we introduce a suite of learning techniques for NeSy-EBMs. Importantly, NeSy-EBMs allow the derivation of general expressions for gradients of prominent learning losses, and we provide four learning approaches that leverage methods from multiple domains, including bilevel and stochastic policy optimization. Finally, we present Neural Probabilistic Soft Logic (NeuPSL), an open-source NeSy-EBM library designed for scalability and expressivity, facilitating real-world application of NeSy systems. Through extensive empirical analysis across multiple datasets, we demonstrate the practical advantages of NeSy-EBMs in various tasks, including image classification, graph node labeling, autonomous vehicle situation awareness, and question answering.

Convex and Bilevel Optimization for Neuro-Symbolic Inference and Learning

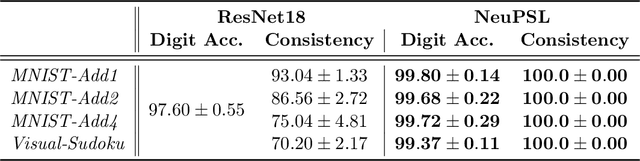
We address a key challenge for neuro-symbolic (NeSy) systems by leveraging convex and bilevel optimization techniques to develop a general gradient-based framework for end-to-end neural and symbolic parameter learning. The applicability of our framework is demonstrated with NeuPSL, a state-of-the-art NeSy architecture. To achieve this, we propose a smooth primal and dual formulation of NeuPSL inference and show learning gradients are functions of the optimal dual variables. Additionally, we develop a dual block coordinate descent algorithm for the new formulation that naturally exploits warm-starts. This leads to over 100x learning runtime improvements over the current best NeuPSL inference method. Finally, we provide extensive empirical evaluations across $8$ datasets covering a range of tasks and demonstrate our learning framework achieves up to a 16% point prediction performance improvement over alternative learning methods.

Optimally Teaching a Linear Behavior Cloning Agent

We study optimal teaching of Linear Behavior Cloning (LBC) learners. In this setup, the teacher can select which states to demonstrate to an LBC learner. The learner maintains a version space of infinite linear hypotheses consistent with the demonstration. The goal of the teacher is to teach a realizable target policy to the learner using minimum number of state demonstrations. This number is known as the Teaching Dimension(TD). We present a teaching algorithm called ``Teach using Iterative Elimination(TIE)" that achieves instance optimal TD. However, we also show that finding optimal teaching set computationally is NP-hard. We further provide an approximation algorithm that guarantees an approximation ratio of $\log(|A|-1)$ on the teaching dimension. Finally, we provide experimental results to validate the efficiency and effectiveness of our algorithm.

Cut your Losses with Squentropy

Nearly all practical neural models for classification are trained using cross-entropy loss. Yet this ubiquitous choice is supported by little theoretical or empirical evidence. Recent work (Hui & Belkin, 2020) suggests that training using the (rescaled) square loss is often superior in terms of the classification accuracy. In this paper we propose the "squentropy" loss, which is the sum of two terms: the cross-entropy loss and the average square loss over the incorrect classes. We provide an extensive set of experiments on multi-class classification problems showing that the squentropy loss outperforms both the pure cross entropy and rescaled square losses in terms of the classification accuracy. We also demonstrate that it provides significantly better model calibration than either of these alternative losses and, furthermore, has less variance with respect to the random initialization. Additionally, in contrast to the square loss, squentropy loss can typically be trained using exactly the same optimization parameters, including the learning rate, as the standard cross-entropy loss, making it a true "plug-and-play" replacement. Finally, unlike the rescaled square loss, multiclass squentropy contains no parameters that need to be adjusted.

A Fully First-Order Method for Stochastic Bilevel Optimization

We consider stochastic unconstrained bilevel optimization problems when only the first-order gradient oracles are available. While numerous optimization methods have been proposed for tackling bilevel problems, existing methods either tend to require possibly expensive calculations regarding Hessians of lower-level objectives, or lack rigorous finite-time performance guarantees. In this work, we propose a Fully First-order Stochastic Approximation (F2SA) method, and study its non-asymptotic convergence properties. Specifically, we show that F2SA converges to an $\epsilon$-stationary solution of the bilevel problem after $\epsilon^{-7/2}, \epsilon^{-5/2}$, and $\epsilon^{-3/2}$ iterations (each iteration using $O(1)$ samples) when stochastic noises are in both level objectives, only in the upper-level objective, and not present (deterministic settings), respectively. We further show that if we employ momentum-assisted gradient estimators, the iteration complexities can be improved to $\epsilon^{-5/2}, \epsilon^{-4/2}$, and $\epsilon^{-3/2}$, respectively. We demonstrate even superior practical performance of the proposed method over existing second-order based approaches on MNIST data-hypercleaning experiments.

BOME! Bilevel Optimization Made Easy: A Simple First-Order Approach

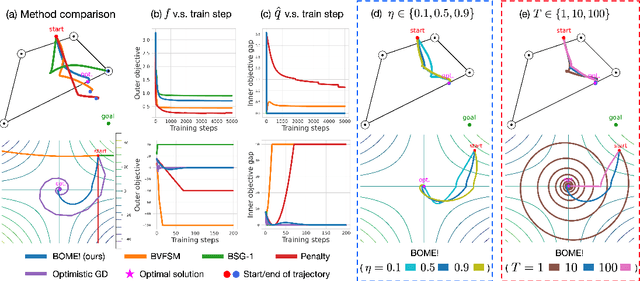
Bilevel optimization (BO) is useful for solving a variety of important machine learning problems including but not limited to hyperparameter optimization, meta-learning, continual learning, and reinforcement learning. Conventional BO methods need to differentiate through the low-level optimization process with implicit differentiation, which requires expensive calculations related to the Hessian matrix. There has been a recent quest for first-order methods for BO, but the methods proposed to date tend to be complicated and impractical for large-scale deep learning applications. In this work, we propose a simple first-order BO algorithm that depends only on first-order gradient information, requires no implicit differentiation, and is practical and efficient for large-scale non-convex functions in deep learning. We provide non-asymptotic convergence analysis of the proposed method to stationary points for non-convex objectives and present empirical results that show its superior practical performance.

On the Global Convergence of Gradient Descent for multi-layer ResNets in the mean-field regime

Finding the optimal configuration of parameters in ResNet is a nonconvex minimization problem, but first-order methods nevertheless find the global optimum in the overparameterized regime. We study this phenomenon with mean-field analysis, by translating the training process of ResNet to a gradient-flow partial differential equation (PDE) and examining the convergence properties of this limiting process. The activation function is assumed to be $2$-homogeneous or partially $1$-homogeneous; the regularized ReLU satisfies the latter condition. We show that if the ResNet is sufficiently large, with depth and width depending algebraically on the accuracy and confidence levels, first-order optimization methods can find global minimizers that fit the training data.

Overparameterization of deep ResNet: zero loss and mean-field analysis

Finding parameters in a deep neural network (NN) that fit training data is a nonconvex optimization problem, but a basic first-order optimization method (gradient descent) finds a global solution with perfect fit in many practical situations. We examine this phenomenon for the case of Residual Neural Networks (ResNet) with smooth activation functions in a limiting regime in which both the number of layers (depth) and the number of neurons in each layer (width) go to infinity. First, we use a mean-field-limit argument to prove that the gradient descent for parameter training becomes a partial differential equation (PDE) that characterizes gradient flow for a probability distribution in the large-NN limit. Next, we show that the solution to the PDE converges in the training time to a zero-loss solution. Together, these results imply that training of the ResNet also gives a near-zero loss if the Resnet is large enough. We give estimates of the depth and width needed to reduce the loss below a given threshold, with high probability.

Stochastic Learning for Sparse Discrete Markov Random Fields with Controlled Gradient Approximation Error

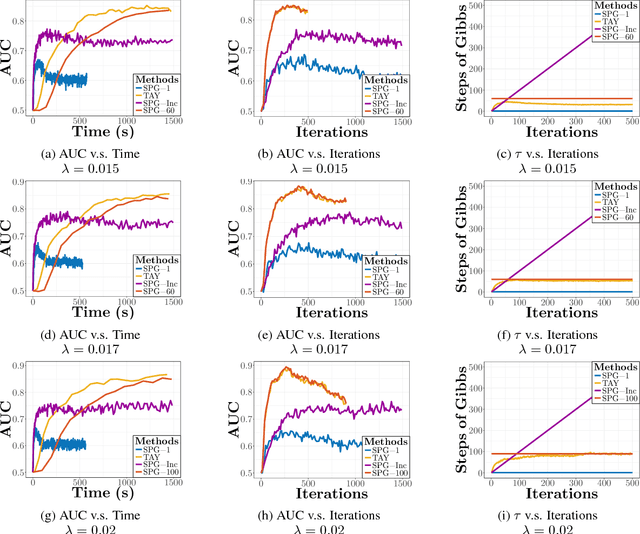
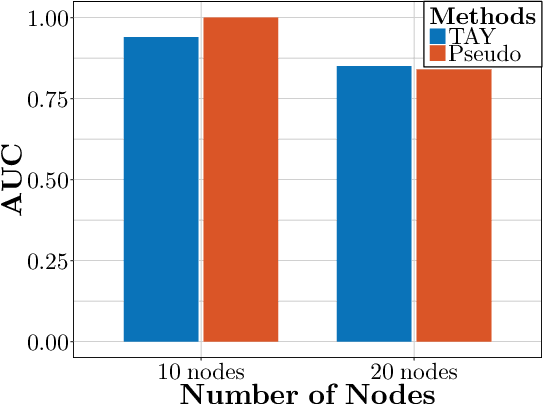
We study the $L_1$-regularized maximum likelihood estimator/estimation (MLE) problem for discrete Markov random fields (MRFs), where efficient and scalable learning requires both sparse regularization and approximate inference. To address these challenges, we consider a stochastic learning framework called stochastic proximal gradient (SPG; Honorio 2012a, Atchade et al. 2014,Miasojedow and Rejchel 2016). SPG is an inexact proximal gradient algorithm [Schmidtet al., 2011], whose inexactness stems from the stochastic oracle (Gibbs sampling) for gradient approximation - exact gradient evaluation is infeasible in general due to the NP-hard inference problem for discrete MRFs [Koller and Friedman, 2009]. Theoretically, we provide novel verifiable bounds to inspect and control the quality of gradient approximation. Empirically, we propose the tighten asymptotically (TAY) learning strategy based on the verifiable bounds to boost the performance of SPG.

Computing Estimators of Dantzig Selector type via Column and Constraint Generation

We consider a class of linear-programming based estimators in reconstructing a sparse signal from linear measurements. Specific formulations of the reconstruction problem considered here include Dantzig selector, basis pursuit (for the case in which the measurements contain no errors), and the fused Dantzig selector (for the case in which the underlying signal is piecewise constant). In spite of being estimators central to sparse signal processing and machine learning, solving these linear programming problems for large scale instances remains a challenging task, thereby limiting their usage in practice. We show that classic constraint- and column-generation techniques from large scale linear programming, when used in conjunction with a commercial implementation of the simplex method, and initialized with the solution from a closely-related Lasso formulation, yields solutions with high efficiency in many settings.