Private Heterogeneous Federated Learning Without a Trusted Server Revisited: Error-Optimal and Communication-Efficient Algorithms for Convex Losses

We revisit the problem of federated learning (FL) with private data from people who do not trust the server or other silos/clients. In this context, every silo (e.g. hospital) has data from several people (e.g. patients) and needs to protect the privacy of each person's data (e.g. health records), even if the server and/or other silos try to uncover this data. Inter-Silo Record-Level Differential Privacy (ISRL-DP) prevents each silo's data from being leaked, by requiring that silo i's communications satisfy item-level differential privacy. Prior work arXiv:2203.06735 characterized the optimal excess risk bounds for ISRL-DP algorithms with homogeneous (i.i.d.) silo data and convex loss functions. However, two important questions were left open: (1) Can the same excess risk bounds be achieved with heterogeneous (non-i.i.d.) silo data? (2) Can the optimal risk bounds be achieved with fewer communication rounds? In this paper, we give positive answers to both questions. We provide novel ISRL-DP FL algorithms that achieve the optimal excess risk bounds in the presence of heterogeneous silo data. Moreover, our algorithms are more communication-efficient than the prior state-of-the-art. For smooth loss functions, our algorithm achieves the optimal excess risk bound and has communication complexity that matches the non-private lower bound. Additionally, our algorithms are more computationally efficient than the previous state-of-the-art.

A Mathematical Framework, a Taxonomy of Modeling Paradigms, and a Suite of Learning Techniques for Neural-Symbolic Systems

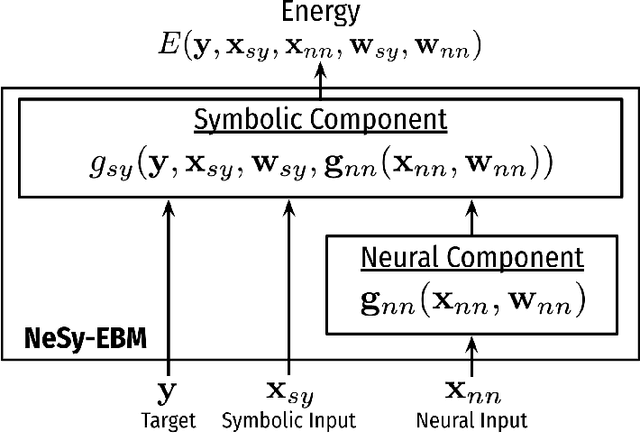
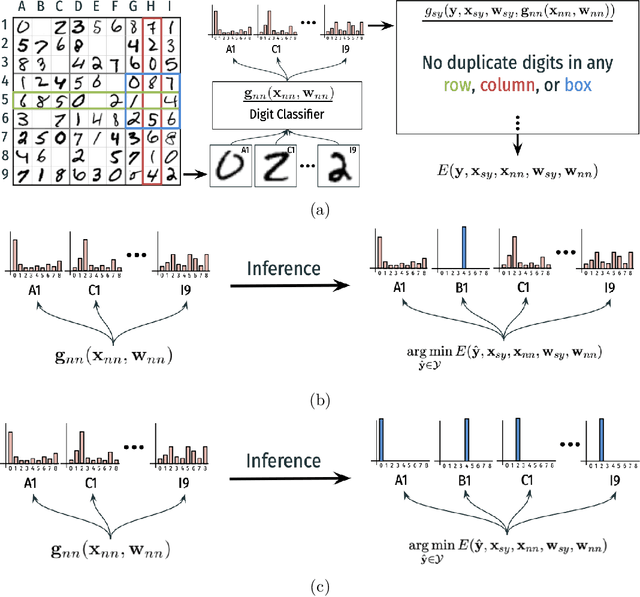
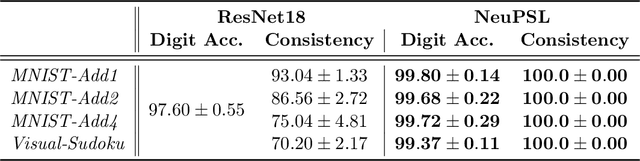
The field of Neural-Symbolic (NeSy) systems is growing rapidly. Proposed approaches show great promise in achieving symbiotic unions of neural and symbolic methods. However, each NeSy system differs in fundamental ways. There is a pressing need for a unifying theory to illuminate the commonalities and differences in approaches and enable further progress. In this paper, we introduce Neural-Symbolic Energy-Based Models (NeSy-EBMs), a unifying mathematical framework for discriminative and generative modeling with probabilistic and non-probabilistic NeSy approaches. We utilize NeSy-EBMs to develop a taxonomy of modeling paradigms focusing on a system's neural-symbolic interface and reasoning capabilities. Additionally, we introduce a suite of learning techniques for NeSy-EBMs. Importantly, NeSy-EBMs allow the derivation of general expressions for gradients of prominent learning losses, and we provide four learning approaches that leverage methods from multiple domains, including bilevel and stochastic policy optimization. Finally, we present Neural Probabilistic Soft Logic (NeuPSL), an open-source NeSy-EBM library designed for scalability and expressivity, facilitating real-world application of NeSy systems. Through extensive empirical analysis across multiple datasets, we demonstrate the practical advantages of NeSy-EBMs in various tasks, including image classification, graph node labeling, autonomous vehicle situation awareness, and question answering.

Convex and Bilevel Optimization for Neuro-Symbolic Inference and Learning

We address a key challenge for neuro-symbolic (NeSy) systems by leveraging convex and bilevel optimization techniques to develop a general gradient-based framework for end-to-end neural and symbolic parameter learning. The applicability of our framework is demonstrated with NeuPSL, a state-of-the-art NeSy architecture. To achieve this, we propose a smooth primal and dual formulation of NeuPSL inference and show learning gradients are functions of the optimal dual variables. Additionally, we develop a dual block coordinate descent algorithm for the new formulation that naturally exploits warm-starts. This leads to over 100x learning runtime improvements over the current best NeuPSL inference method. Finally, we provide extensive empirical evaluations across $8$ datasets covering a range of tasks and demonstrate our learning framework achieves up to a 16% point prediction performance improvement over alternative learning methods.

Differentially Private Optimization for Smooth Nonconvex ERM

We develop simple differentially private optimization algorithms that move along directions of (expected) descent to find an approximate second-order solution for nonconvex ERM. We use line search, mini-batching, and a two-phase strategy to improve the speed and practicality of the algorithm. Numerical experiments demonstrate the effectiveness of these approaches.