Optimally Teaching a Linear Behavior Cloning Agent

We study optimal teaching of Linear Behavior Cloning (LBC) learners. In this setup, the teacher can select which states to demonstrate to an LBC learner. The learner maintains a version space of infinite linear hypotheses consistent with the demonstration. The goal of the teacher is to teach a realizable target policy to the learner using minimum number of state demonstrations. This number is known as the Teaching Dimension(TD). We present a teaching algorithm called ``Teach using Iterative Elimination(TIE)" that achieves instance optimal TD. However, we also show that finding optimal teaching set computationally is NP-hard. We further provide an approximation algorithm that guarantees an approximation ratio of $\log(|A|-1)$ on the teaching dimension. Finally, we provide experimental results to validate the efficiency and effectiveness of our algorithm.

Provable Defense against Backdoor Policies in Reinforcement Learning

We propose a provable defense mechanism against backdoor policies in reinforcement learning under subspace trigger assumption. A backdoor policy is a security threat where an adversary publishes a seemingly well-behaved policy which in fact allows hidden triggers. During deployment, the adversary can modify observed states in a particular way to trigger unexpected actions and harm the agent. We assume the agent does not have the resources to re-train a good policy. Instead, our defense mechanism sanitizes the backdoor policy by projecting observed states to a 'safe subspace', estimated from a small number of interactions with a clean (non-triggered) environment. Our sanitized policy achieves $\epsilon$ approximate optimality in the presence of triggers, provided the number of clean interactions is $O\left(\frac{D}{(1-\gamma)^4 \epsilon^2}\right)$ where $\gamma$ is the discounting factor and $D$ is the dimension of state space. Empirically, we show that our sanitization defense performs well on two Atari game environments.

The Teaching Dimension of Q-learning

In this paper, we initiate the study of sample complexity of teaching, termed as "teaching dimension" (TDim) in the literature, for Q-learning. While the teaching dimension of supervised learning has been studied extensively, these results do not extend to reinforcement learning due to the temporal constraints posed by the underlying Markov Decision Process environment. We characterize the TDim of Q-learning under different teachers with varying control over the environment, and present matching optimal teaching algorithms. Our TDim results provide the minimum number of samples needed for reinforcement learning, thus complementing standard PAC-style RL sample complexity analysis. Our teaching algorithms have the potential to speed up RL agent learning in applications where a helpful teacher is available.

On the relationship between multitask neural networks and multitask Gaussian Processes

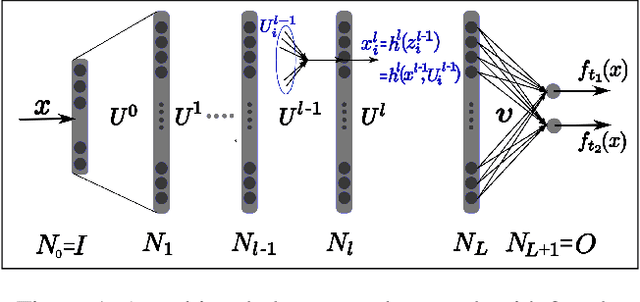
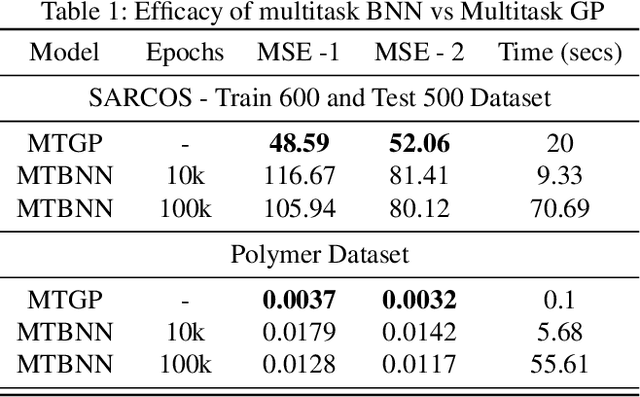
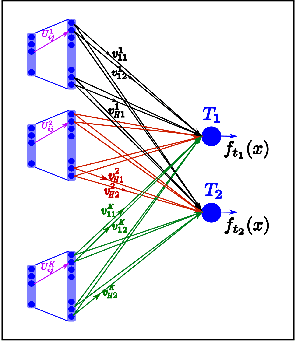
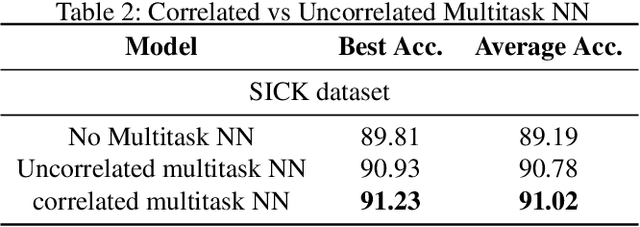
Despite the effectiveness of multitask deep neural network (MTDNN), there is a limited theoretical understanding on how the information is shared across different tasks in MTDNN. In this work, we establish a formal connection between MTDNN with infinitely-wide hidden layers and multitask Gaussian Process (GP). We derive multitask GP kernels corresponding to both single-layer and deep multitask Bayesian neural networks (MTBNN) and show that information among different tasks is shared primarily due to correlation across last layer weights of MTBNN and shared hyper-parameters, which is contrary to the popular hypothesis that information is shared because of shared intermediate layer weights. Our construction enables using multitask GP to perform efficient Bayesian inference for the equivalent MTDNN with infinitely-wide hidden layers. Prior work on the connection between deep neural networks and GP for single task settings can be seen as special cases of our construction. We also present an adaptive multitask neural network architecture that corresponds to a multitask GP with more flexible kernels, such as Linear Model of Coregionalization (LMC) and Cross-Coregionalization (CC) kernels. We provide experimental results to further illustrate these ideas on synthetic and real datasets.