On the relationship between multitask neural networks and multitask Gaussian Processes
Paper and Code
Dec 12, 2019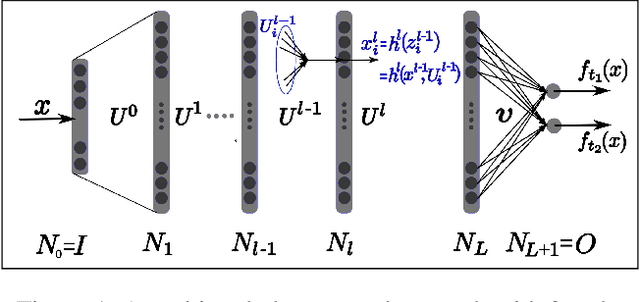
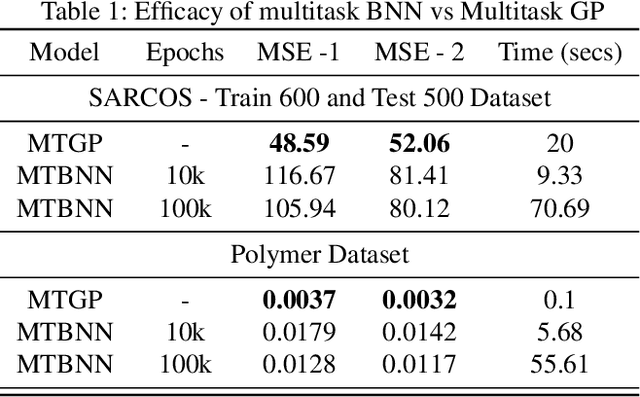
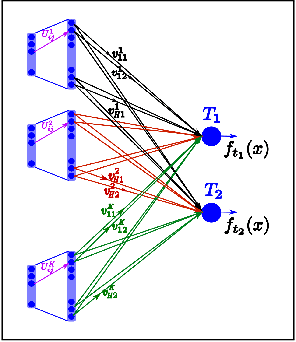
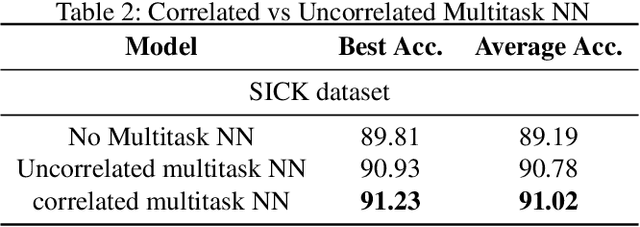
Despite the effectiveness of multitask deep neural network (MTDNN), there is a limited theoretical understanding on how the information is shared across different tasks in MTDNN. In this work, we establish a formal connection between MTDNN with infinitely-wide hidden layers and multitask Gaussian Process (GP). We derive multitask GP kernels corresponding to both single-layer and deep multitask Bayesian neural networks (MTBNN) and show that information among different tasks is shared primarily due to correlation across last layer weights of MTBNN and shared hyper-parameters, which is contrary to the popular hypothesis that information is shared because of shared intermediate layer weights. Our construction enables using multitask GP to perform efficient Bayesian inference for the equivalent MTDNN with infinitely-wide hidden layers. Prior work on the connection between deep neural networks and GP for single task settings can be seen as special cases of our construction. We also present an adaptive multitask neural network architecture that corresponds to a multitask GP with more flexible kernels, such as Linear Model of Coregionalization (LMC) and Cross-Coregionalization (CC) kernels. We provide experimental results to further illustrate these ideas on synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge