Andrew Zheng
Differences-in-Neighbors for Network Interference in Experiments
Mar 04, 2025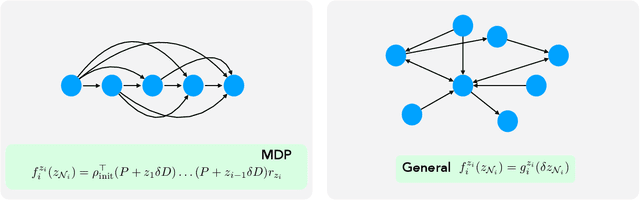

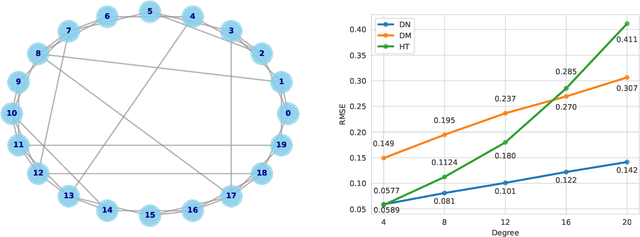
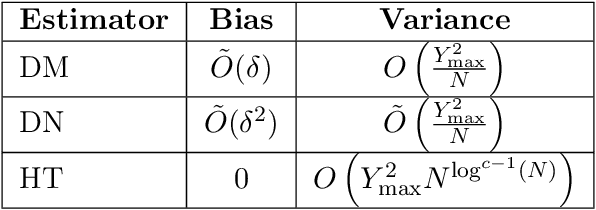
Abstract:Experiments in online platforms frequently suffer from network interference, in which a treatment applied to a given unit affects outcomes for other units connected via the platform. This SUTVA violation biases naive approaches to experiment design and estimation. A common solution is to reduce interference by clustering connected units, and randomizing treatments at the cluster level, typically followed by estimation using one of two extremes: either a simple difference-in-means (DM) estimator, which ignores remaining interference; or an unbiased Horvitz-Thompson (HT) estimator, which eliminates interference at great cost in variance. Even combined with clustered designs, this presents a limited set of achievable bias variance tradeoffs. We propose a new estimator, dubbed Differences-in-Neighbors (DN), designed explicitly to mitigate network interference. Compared to DM estimators, DN achieves bias second order in the magnitude of the interference effect, while its variance is exponentially smaller than that of HT estimators. When combined with clustered designs, DN offers improved bias-variance tradeoffs not achievable by existing approaches. Empirical evaluations on a large-scale social network and a city-level ride-sharing simulator demonstrate the superior performance of DN in experiments at practical scale.
Speeding up Policy Simulation in Supply Chain RL
Jun 04, 2024Abstract:Simulating a single trajectory of a dynamical system under some state-dependent policy is a core bottleneck in policy optimization algorithms. The many inherently serial policy evaluations that must be performed in a single simulation constitute the bulk of this bottleneck. To wit, in applying policy optimization to supply chain optimization (SCO) problems, simulating a single month of a supply chain can take several hours. We present an iterative algorithm for policy simulation, which we dub Picard Iteration. This scheme carefully assigns policy evaluation tasks to independent processes. Within an iteration, a single process evaluates the policy only on its assigned tasks while assuming a certain 'cached' evaluation for other tasks; the cache is updated at the end of the iteration. Implemented on GPUs, this scheme admits batched evaluation of the policy on a single trajectory. We prove that the structure afforded by many SCO problems allows convergence in a small number of iterations, independent of the horizon. We demonstrate practical speedups of 400x on large-scale SCO problems even with a single GPU, and also demonstrate practical efficacy in other RL environments.
Effects of Dataset Sampling Rate for Noise Cancellation through Deep Learning
May 30, 2024Abstract:Background: Active noise cancellation has been a subject of research for decades. Traditional techniques, like the Fast Fourier Transform, have limitations in certain scenarios. This research explores the use of deep neural networks (DNNs) as a superior alternative. Objective: The study aims to determine the effect sampling rate within training data has on lightweight, efficient DNNs that operate within the processing constraints of mobile devices. Methods: We chose the ConvTasNET network for its proven efficiency in speech separation and enhancement. ConvTasNET was trained on datasets such as WHAM!, LibriMix, and the MS-2023 DNS Challenge. The datasets were sampled at rates of 8kHz, 16kHz, and 48kHz to analyze the effect of sampling rate on noise cancellation efficiency and effectiveness. The model was tested on a core-i7 Intel processor from 2023, assessing the network's ability to produce clear audio while filtering out background noise. Results: Models trained at higher sampling rates (48kHz) provided much better evaluation metrics against Total Harmonic Distortion (THD) and Quality Prediction For Generative Neural Speech Codecs (WARP-Q) values, indicating improved audio quality. However, a trade-off was noted with the processing time being longer for higher sampling rates. Conclusions: The Conv-TasNET network, trained on datasets sampled at higher rates like 48kHz, offers a robust solution for mobile devices in achieving noise cancellation through speech separation and enhancement. Future work involves optimizing the model's efficiency further and testing on mobile devices.
Safe Motion Planning for Quadruped Robots Using Density Functions
Dec 14, 2023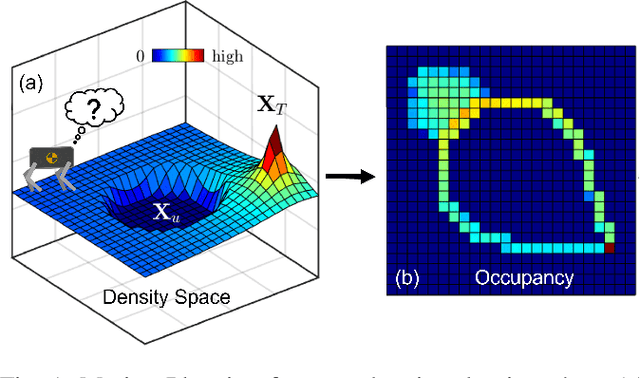
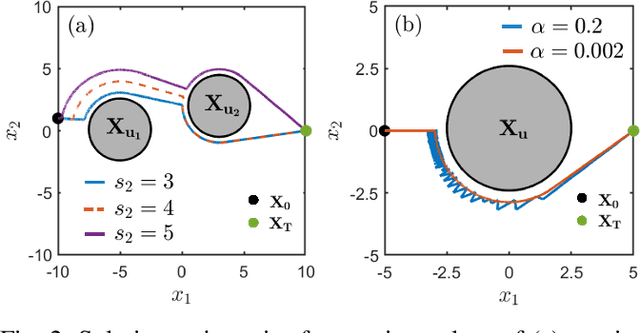
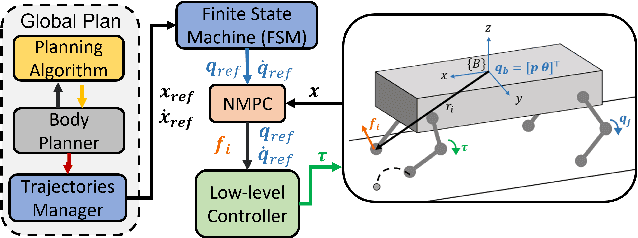
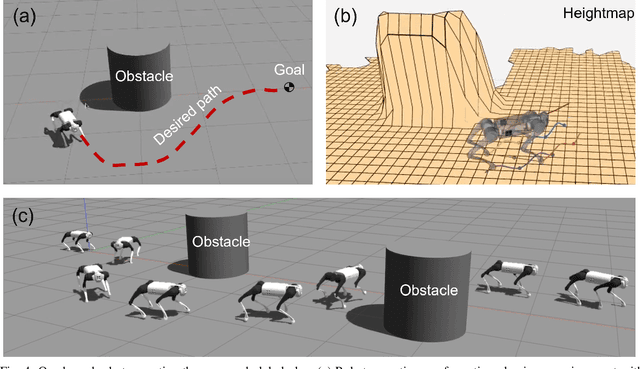
Abstract:This paper presents a motion planning algorithm for quadruped locomotion based on density functions. We decompose the locomotion problem into a high-level density planner and a model predictive controller (MPC). Due to density functions having a physical interpretation through the notion of occupancy, it is intuitive to represent the environment with safety constraints. Hence, there is an ease of use to constructing the planning problem with density. The proposed method uses a simplified model of the robot into an integrator system, where the high-level plan is in a feedback form formulated through an analytically constructed density function. We then use the MPC to optimize the reference trajectory, in which a low-level PID controller is used to obtain the torque level control. The overall framework is implemented in simulation, demonstrating our feedback density planner for legged locomotion. The implementation of work is available at \url{https://github.com/AndrewZheng-1011/legged_planner}
Safety using Analytically Constructed Density Functions
Jun 27, 2023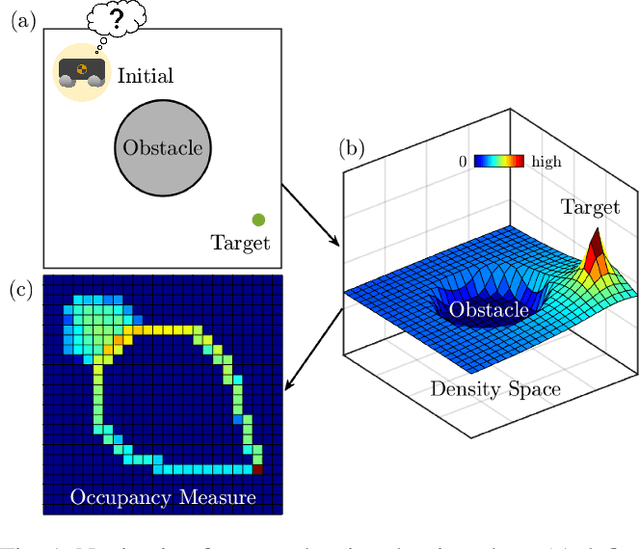
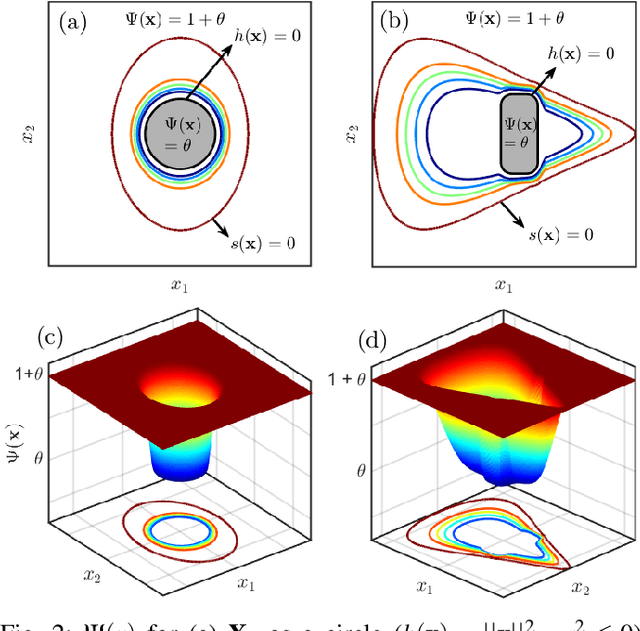
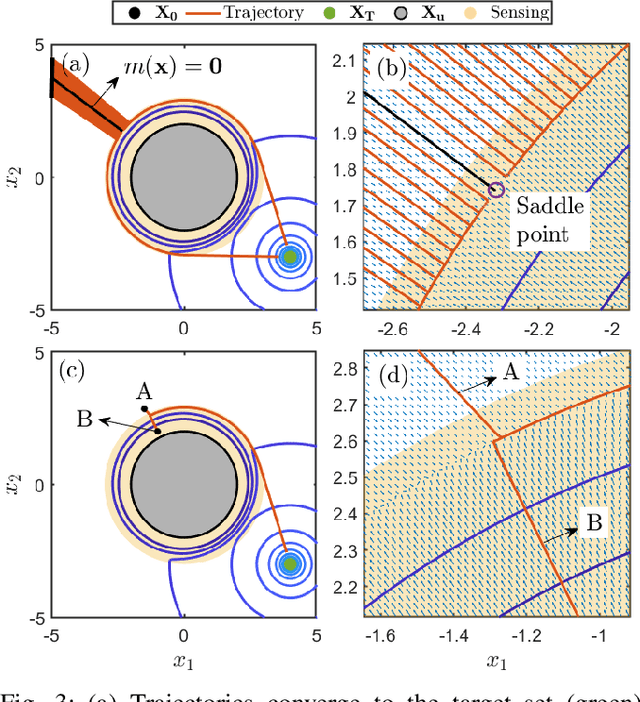
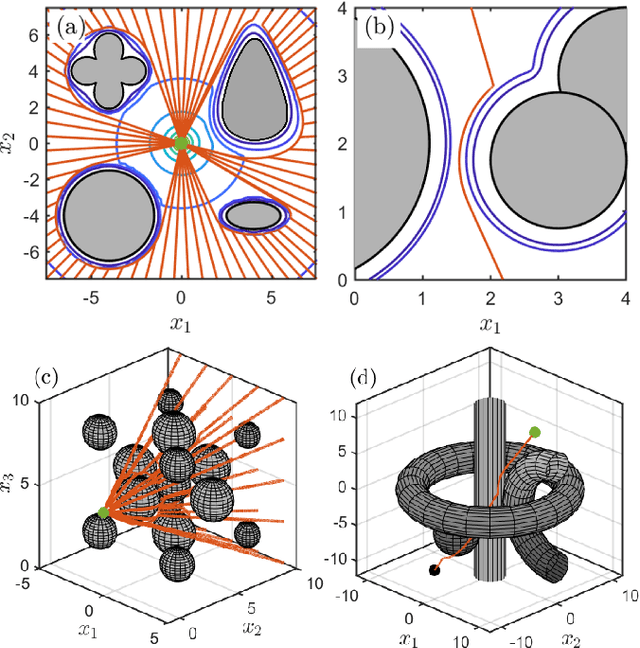
Abstract:This paper presents a novel approach for safe control synthesis using the dual formulation of the navigation problem. The main contribution of this paper is in the analytical construction of density functions for almost everywhere navigation with safety constraints. In contrast to the existing approaches, where density functions are used for the analysis of navigation problems, we use density functions for the synthesis of safe controllers. We provide convergence proof using the proposed density functions for navigation with safety. Further, we use these density functions to design feedback controllers capable of navigating in cluttered environments and high-dimensional configuration spaces. The proposed analytical construction of density functions overcomes the problem associated with navigation functions, which are known to exist but challenging to construct, and potential functions, which suffer from local minima. Application of the developed framework is demonstrated on simple integrator dynamics and fully actuated robotic systems.
Off-Road Navigation of Legged Robots Using Linear Transfer Operators
May 04, 2023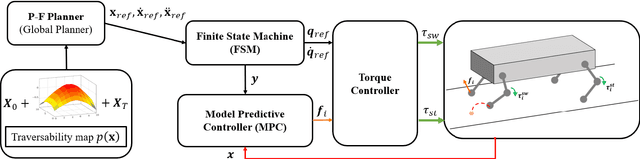
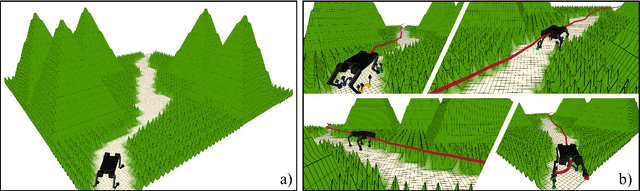
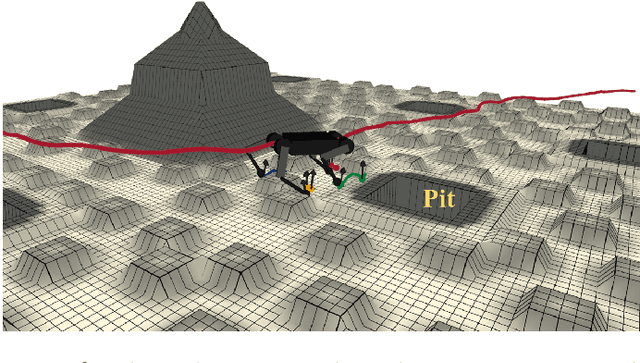
Abstract:This paper presents the implementation of off-road navigation on legged robots using convex optimization through linear transfer operators. Given a traversability measure that captures the off-road environment, we lift the navigation problem into the density space using the Perron-Frobenius (P-F) operator. This allows the problem formulation to be represented as a convex optimization. Due to the operator acting on an infinite-dimensional density space, we use data collected from the terrain to get a finite-dimension approximation of the convex optimization. Results of the optimal trajectory for off-road navigation are compared with a standard iterative planner, where we show how our convex optimization generates a more traversable path for the legged robot compared to the suboptimal iterative planner.
Correcting for Interference in Experiments: A Case Study at Douyin
May 04, 2023



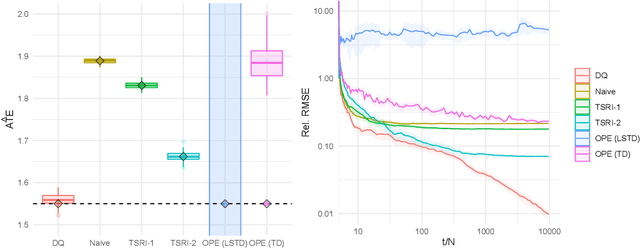
Abstract:Interference is a ubiquitous problem in experiments conducted on two-sided content marketplaces, such as Douyin (China's analog of TikTok). In many cases, creators are the natural unit of experimentation, but creators interfere with each other through competition for viewers' limited time and attention. "Naive" estimators currently used in practice simply ignore the interference, but in doing so incur bias on the order of the treatment effect. We formalize the problem of inference in such experiments as one of policy evaluation. Off-policy estimators, while unbiased, are impractically high variance. We introduce a novel Monte-Carlo estimator, based on "Differences-in-Qs" (DQ) techniques, which achieves bias that is second-order in the treatment effect, while remaining sample-efficient to estimate. On the theoretical side, our contribution is to develop a generalized theory of Taylor expansions for policy evaluation, which extends DQ theory to all major MDP formulations. On the practical side, we implement our estimator on Douyin's experimentation platform, and in the process develop DQ into a truly "plug-and-play" estimator for interference in real-world settings: one which provides robust, low-bias, low-variance treatment effect estimates; admits computationally cheap, asymptotically exact uncertainty quantification; and reduces MSE by 99\% compared to the best existing alternatives in our applications.
Optimal Control for Quadruped Locomotion using LTV MPC
Dec 20, 2022



Abstract:This paper presents a state-of-the-art optimal controller for quadruped locomotion. The robot dynamics is represented using a single rigid body (SRB) model. A linear time-varying model predictive controller (LTV MPC) is proposed by using linearization schemes. Simulation results show that the LTV MPC can execute various gaits, such as trot and crawl, and is capable of tracking desired reference trajectories even under unknown external disturbances. The LTV MPC is implemented as a quadratic program using qpOASES through the CasADi interface at 50 Hz. The proposed MPC can reach up to 1 m/s top speed with an acceleration of 0.5 m/s2 executing a trot gait. The implementation is available at https:// github.com/AndrewZheng-1011/Quad_ConvexMPC
Markovian Interference in Experiments
Jun 09, 2022

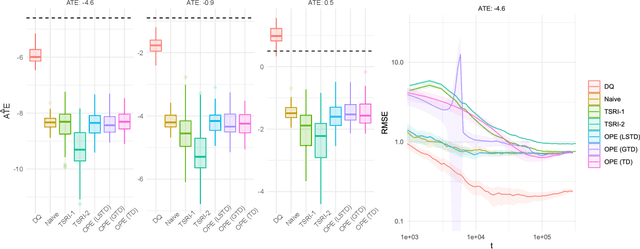
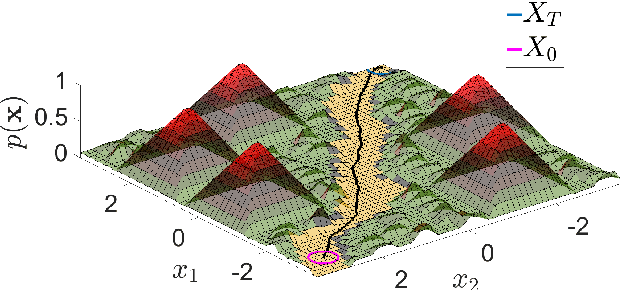
Abstract:We consider experiments in dynamical systems where interventions on some experimental units impact other units through a limiting constraint (such as a limited inventory). Despite outsize practical importance, the best estimators for this `Markovian' interference problem are largely heuristic in nature, and their bias is not well understood. We formalize the problem of inference in such experiments as one of policy evaluation. Off-policy estimators, while unbiased, apparently incur a large penalty in variance relative to state-of-the-art heuristics. We introduce an on-policy estimator: the Differences-In-Q's (DQ) estimator. We show that the DQ estimator can in general have exponentially smaller variance than off-policy evaluation. At the same time, its bias is second order in the impact of the intervention. This yields a striking bias-variance tradeoff so that the DQ estimator effectively dominates state-of-the-art alternatives. From a theoretical perspective, we introduce three separate novel techniques that are of independent interest in the theory of Reinforcement Learning (RL). Our empirical evaluation includes a set of experiments on a city-scale ride-hailing simulator.
Synthetically Controlled Bandits
Feb 14, 2022



Abstract:This paper presents a new dynamic approach to experiment design in settings where, due to interference or other concerns, experimental units are coarse. `Region-split' experiments on online platforms are one example of such a setting. The cost, or regret, of experimentation is a natural concern here. Our new design, dubbed Synthetically Controlled Thompson Sampling (SCTS), minimizes the regret associated with experimentation at no practically meaningful loss to inferential ability. We provide theoretical guarantees characterizing the near-optimal regret of our approach, and the error rates achieved by the corresponding treatment effect estimator. Experiments on synthetic and real world data highlight the merits of our approach relative to both fixed and `switchback' designs common to such experimental settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge