Off-Road Navigation of Legged Robots Using Linear Transfer Operators
Paper and Code
May 04, 2023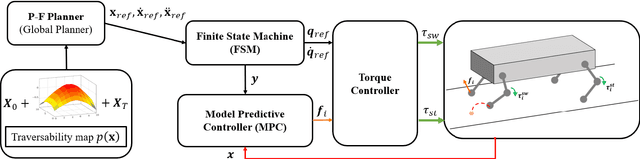
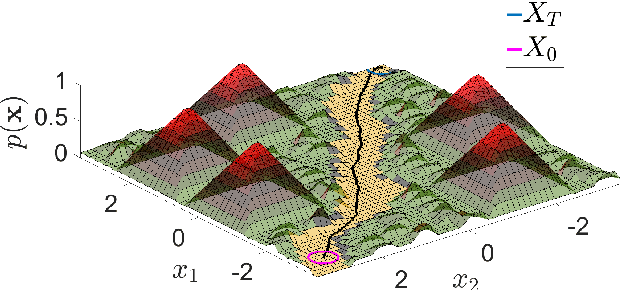
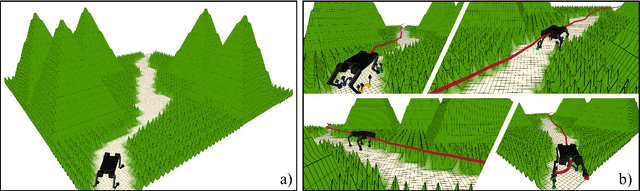
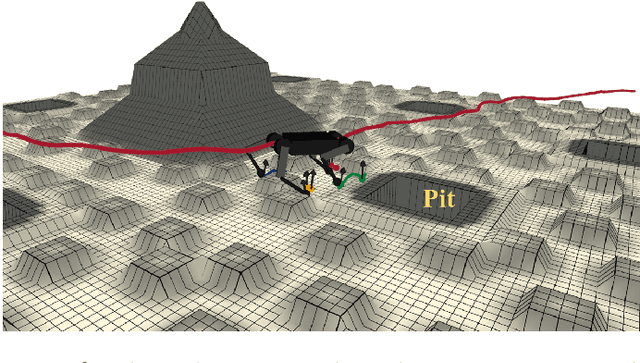
This paper presents the implementation of off-road navigation on legged robots using convex optimization through linear transfer operators. Given a traversability measure that captures the off-road environment, we lift the navigation problem into the density space using the Perron-Frobenius (P-F) operator. This allows the problem formulation to be represented as a convex optimization. Due to the operator acting on an infinite-dimensional density space, we use data collected from the terrain to get a finite-dimension approximation of the convex optimization. Results of the optimal trajectory for off-road navigation are compared with a standard iterative planner, where we show how our convex optimization generates a more traversable path for the legged robot compared to the suboptimal iterative planner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge