Kernel Methods for the Approximation of the Eigenfunctions of the Koopman Operator

The Koopman operator provides a linear framework to study nonlinear dynamical systems. Its spectra offer valuable insights into system dynamics, but the operator can exhibit both discrete and continuous spectra, complicating direct computations. In this paper, we introduce a kernel-based method to construct the principal eigenfunctions of the Koopman operator without explicitly computing the operator itself. These principal eigenfunctions are associated with the equilibrium dynamics, and their eigenvalues match those of the linearization of the nonlinear system at the equilibrium point. We exploit the structure of the principal eigenfunctions by decomposing them into linear and nonlinear components. The linear part corresponds to the left eigenvector of the system's linearization at the equilibrium, while the nonlinear part is obtained by solving a partial differential equation (PDE) using kernel methods. Our approach avoids common issues such as spectral pollution and spurious eigenvalues, which can arise in previous methods. We demonstrate the effectiveness of our algorithm through numerical examples.

Safe Navigation in Dynamic Environments using Density Functions

This work uses density functions for safe navigation in dynamic environments. The dynamic environment consists of time-varying obstacles as well as time-varying target sets. We propose an analytical construction of time-varying density functions to solve these navigation problems. The proposed approach leads to a time-varying feedback controller obtained as a positive gradient of the density function. This paper's main contribution is providing convergence proof using the analytically constructed density function for safe navigation in the presence of a dynamic obstacle set and time-varying target set. The results are the first of this kind developed for a system with integrator dynamics and open up the possibility for application to systems with more complex dynamics using methods based on control density function and inverse kinematic-based control design. We present the application of the developed approach for collision avoidance in multi-agent systems and robotic systems. While the theoretical results are produced for first-order integrator systems, we demonstrate how the framework can be applied for systems with non-trivial dynamics, such as Dubin's car model and fully actuated Euler-Lagrange system with robotics applications.

Digital Twins Meet the Koopman Operator: Data-Driven Learning for Robust Autonomy

Contrary to on-road autonomous navigation, off-road autonomy is complicated by various factors ranging from sensing challenges to terrain variability. In such a milieu, data-driven approaches have been commonly employed to capture intricate vehicle-environment interactions effectively. However, the success of data-driven methods depends crucially on the quality and quantity of data, which can be compromised by large variability in off-road environments. To address these concerns, we present a novel workflow to recreate the exact vehicle and its target operating conditions digitally for domain-specific data generation. This enables us to effectively model off-road vehicle dynamics from simulation data using the Koopman operator theory, and employ the obtained models for local motion planning and optimal vehicle control. The capabilities of the proposed methodology are demonstrated through an autonomous navigation problem of a 1:5 scale vehicle, where a terrain-informed planner is employed for global mission planning. Results indicate a substantial improvement in off-road navigation performance with the proposed algorithm (5.84x) and underscore the efficacy of digital twinning in terms of improving the sample efficiency (3.2x) and reducing the sim2real gap (5.2%).

Safe Motion Planning for Quadruped Robots Using Density Functions

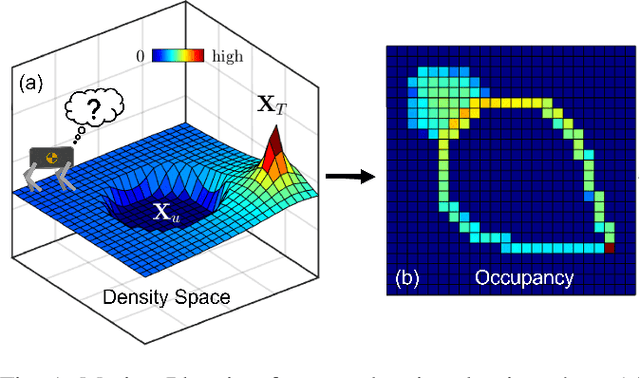
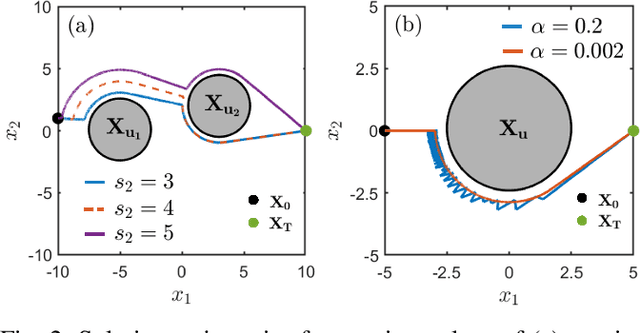
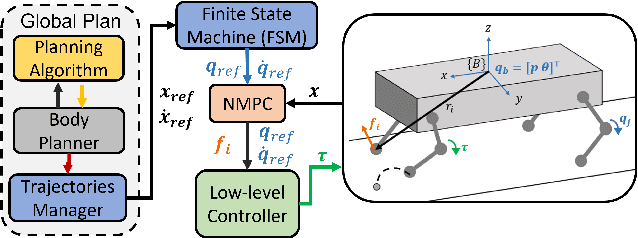
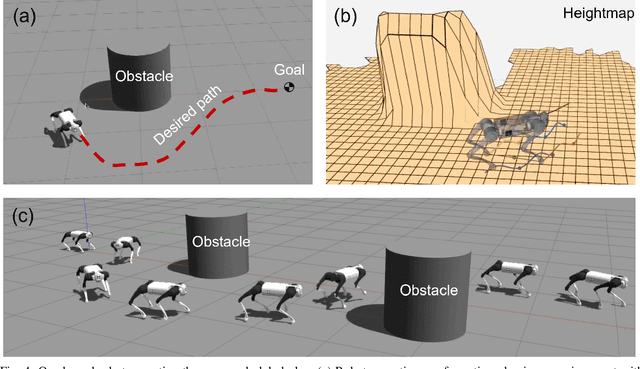
This paper presents a motion planning algorithm for quadruped locomotion based on density functions. We decompose the locomotion problem into a high-level density planner and a model predictive controller (MPC). Due to density functions having a physical interpretation through the notion of occupancy, it is intuitive to represent the environment with safety constraints. Hence, there is an ease of use to constructing the planning problem with density. The proposed method uses a simplified model of the robot into an integrator system, where the high-level plan is in a feedback form formulated through an analytically constructed density function. We then use the MPC to optimize the reference trajectory, in which a low-level PID controller is used to obtain the torque level control. The overall framework is implemented in simulation, demonstrating our feedback density planner for legged locomotion. The implementation of work is available at \url{https://github.com/AndrewZheng-1011/legged_planner}

Safety using Analytically Constructed Density Functions

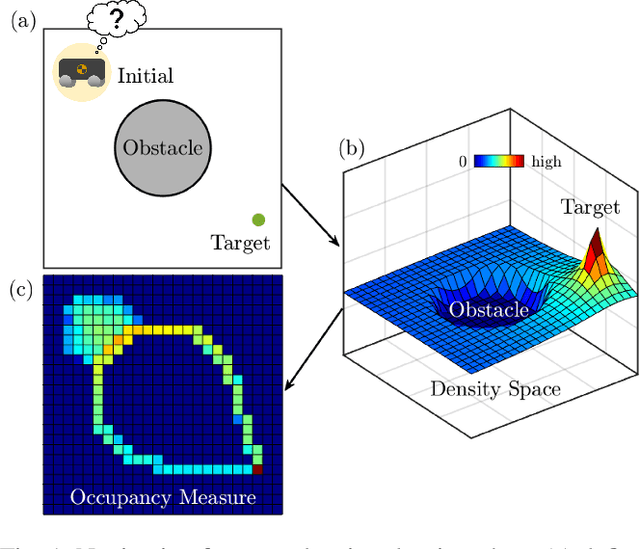
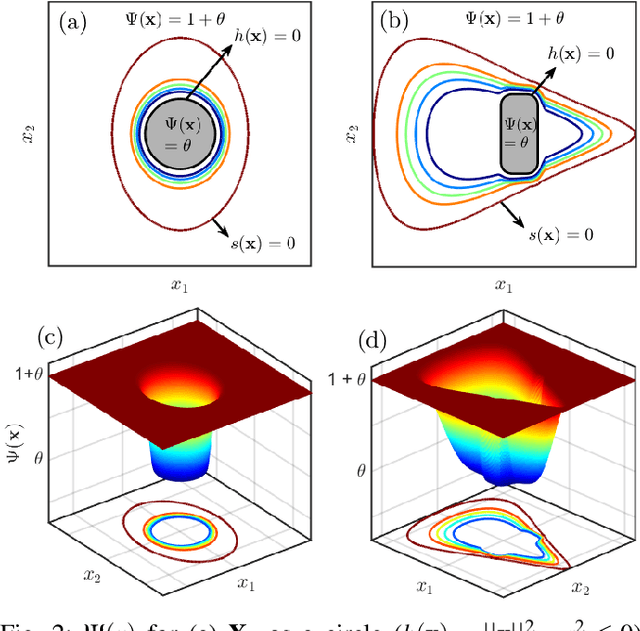
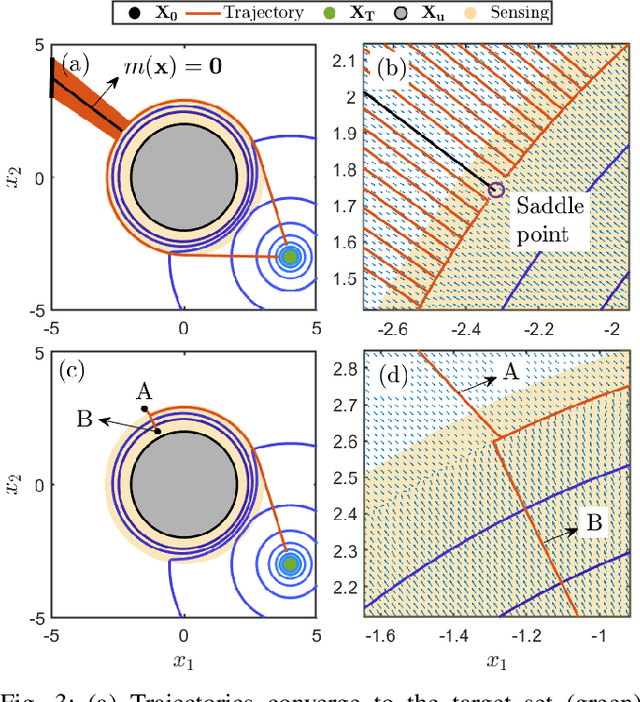
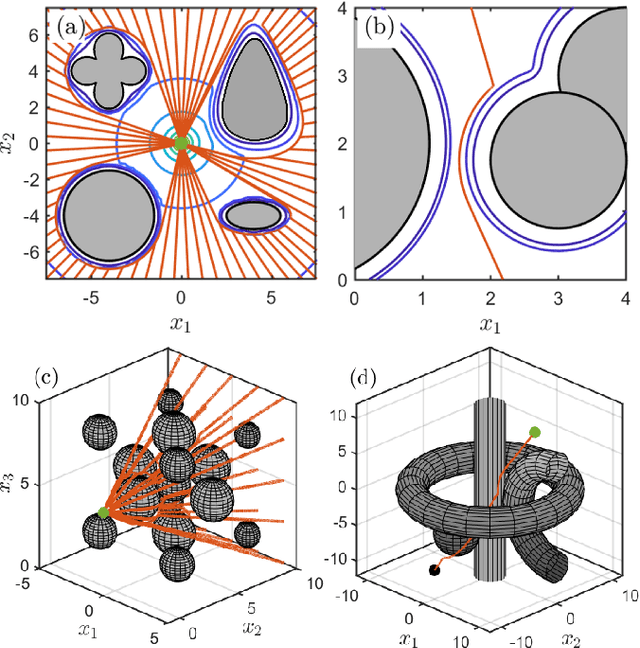
This paper presents a novel approach for safe control synthesis using the dual formulation of the navigation problem. The main contribution of this paper is in the analytical construction of density functions for almost everywhere navigation with safety constraints. In contrast to the existing approaches, where density functions are used for the analysis of navigation problems, we use density functions for the synthesis of safe controllers. We provide convergence proof using the proposed density functions for navigation with safety. Further, we use these density functions to design feedback controllers capable of navigating in cluttered environments and high-dimensional configuration spaces. The proposed analytical construction of density functions overcomes the problem associated with navigation functions, which are known to exist but challenging to construct, and potential functions, which suffer from local minima. Application of the developed framework is demonstrated on simple integrator dynamics and fully actuated robotic systems.

SE Koopman-MPC: Data-driven Learning and Control of Quadrotor UAVs

In this paper, we propose a novel data-driven approach for learning and control of quadrotor UAVs based on the Koopman operator and extended dynamic mode decomposition (EDMD). Building observables for EDMD based on conventional methods like Euler angles or quaternions to represent orientation is known to involve singularities. To address this issue, we employ a set of physics-informed observables based on the underlying topology of the nonlinear system. We use rotation matrices to directly represent the orientation dynamics and obtain a lifted linear representation of the nonlinear quadrotor dynamics in the SE(3) manifold. This EDMD model leads to accurate prediction and can generalize to several validation sets. Further, we design a linear model predictive controller (MPC) based on the proposed EDMD model to track agile reference trajectories. Simulation results show that the proposed MPC controller can run as fast as 100 Hz and is able to track arbitrary reference trajectories with good accuracy. Implementation details can be found in \url{https://github.com/sriram-2502/KoopmanMPC_Quadrotor}

Off-Road Navigation of Legged Robots Using Linear Transfer Operators

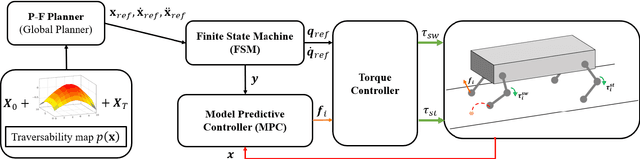
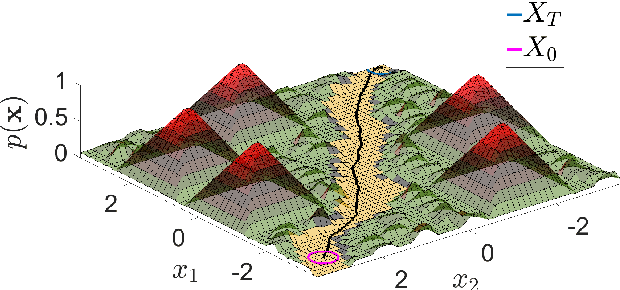
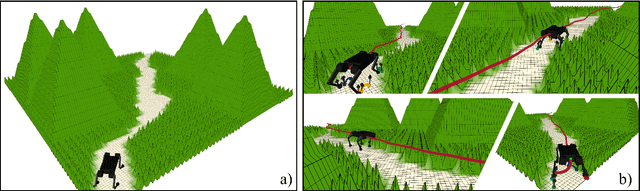
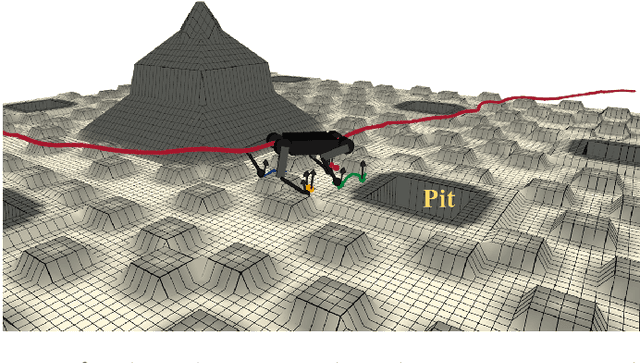
This paper presents the implementation of off-road navigation on legged robots using convex optimization through linear transfer operators. Given a traversability measure that captures the off-road environment, we lift the navigation problem into the density space using the Perron-Frobenius (P-F) operator. This allows the problem formulation to be represented as a convex optimization. Due to the operator acting on an infinite-dimensional density space, we use data collected from the terrain to get a finite-dimension approximation of the convex optimization. Results of the optimal trajectory for off-road navigation are compared with a standard iterative planner, where we show how our convex optimization generates a more traversable path for the legged robot compared to the suboptimal iterative planner.

Deep Learning of Koopman Representation for Control

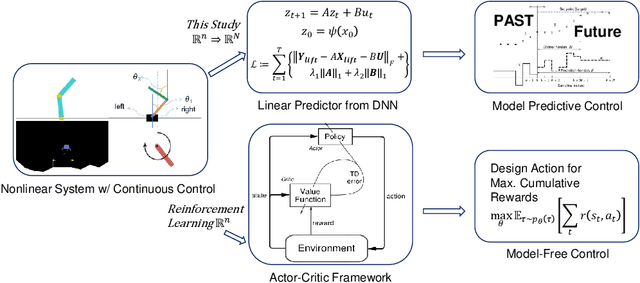
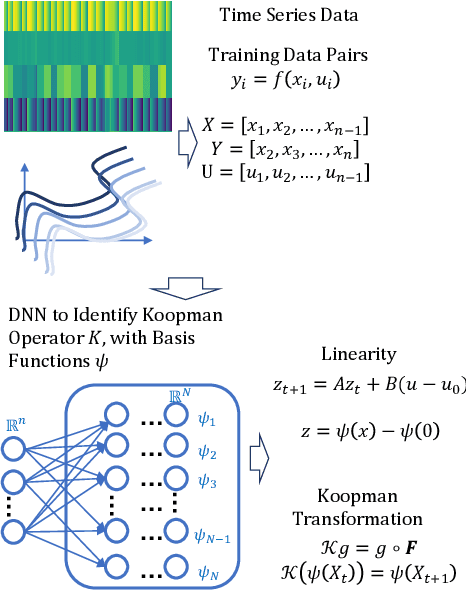
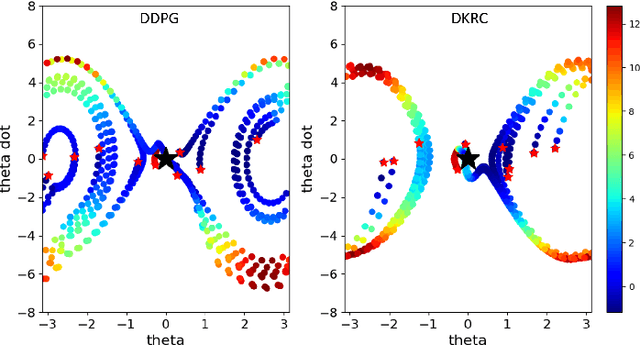
We develop a data-driven, model-free approach for the optimal control of the dynamical system. The proposed approach relies on the Deep Neural Network (DNN) based learning of Koopman operator for the purpose of control. In particular, DNN is employed for the data-driven identification of basis function used in the linear lifting of nonlinear control system dynamics. The controller synthesis is purely data-driven and does not rely on a priori domain knowledge. The OpenAI Gym environment, employed for Reinforcement Learning-based control design, is used for data generation and learning of Koopman operator in control setting. The method is applied to two classic dynamical systems on OpenAI Gym environment to demonstrate the capability.

A convex data-driven approach for nonlinear control synthesis

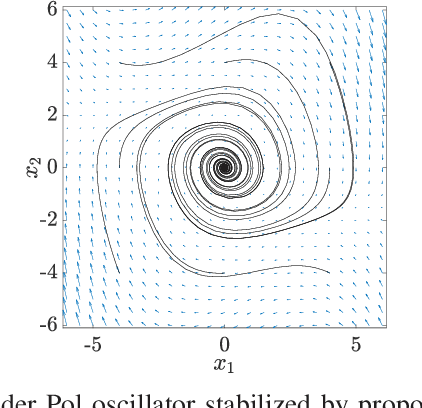
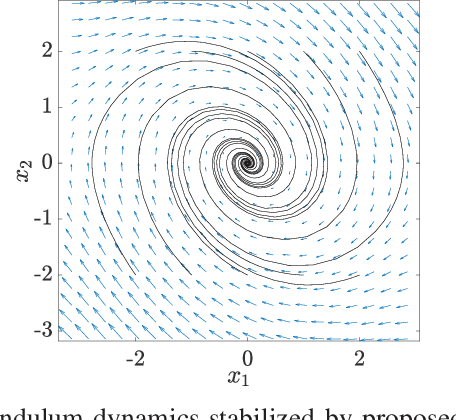
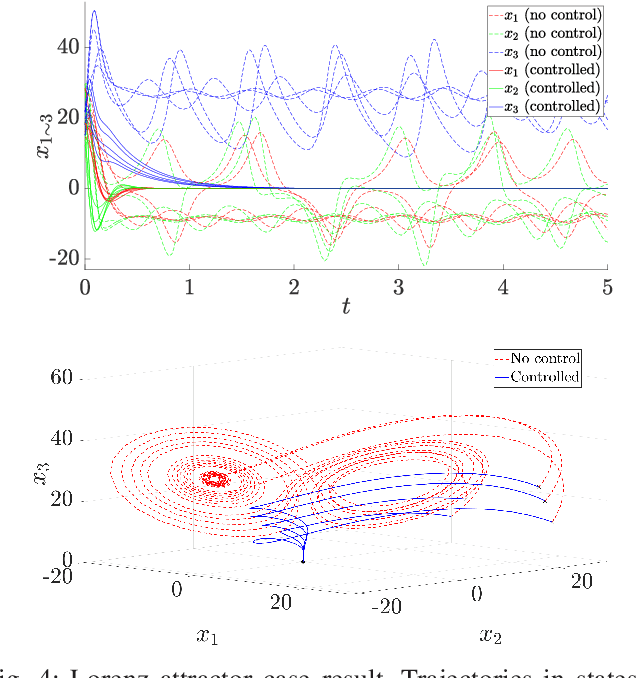
We consider a class of nonlinear control synthesis problems where the underlying mathematical models are not explicitly known. We propose a data-driven approach to stabilize the systems when only sample trajectories of the dynamics are accessible. Our method is founded on the density function based almost everywhere stability certificate that is dual to the Lyapunov function for dynamic systems. Unlike Lyapunov based methods, density functions lead to a convex formulation for a joint search of the control strategy and the stability certificate. This type of convex problem can be solved efficiently by invoking the machinery of the sum of squares (SOS). For the data-driven part, we exploit the fact that the duality results in the stability theory of the dynamical system can be understood using linear Perron-Frobenius and Koopman operators. This connection allows us to use data-driven methods developed to approximate these operators combined with the SOS techniques for the convex formulation of control synthesis. The efficacy of the proposed approach is demonstrated through several examples.

A Saddle-Point Dynamical System Approach for Robust Deep Learning

We propose a novel discrete-time dynamical system-based framework for achieving adversarial robustness in machine learning models. Our algorithm is originated from robust optimization, which aims to find the saddle point of a min-max optimization problem in the presence of uncertainties. The robust learning problem is formulated as a robust optimization problem, and we introduce a discrete-time algorithm based on a saddle-point dynamical system (SDS) to solve this problem. Under the assumptions that the cost function is convex and uncertainties enter concavely in the robust learning problem, we analytically show that using a diminishing step-size, the stochastic version of our algorithm, SSDS converges asymptotically to the robust optimal solution. The algorithm is deployed for the training of adversarially robust deep neural networks. Although such training involves highly non-convex non-concave robust optimization problems, empirical results show that the algorithm can achieve significant robustness for deep learning. We compare the performance of our SSDS model to other state-of-the-art robust models, e.g., trained using the projected gradient descent (PGD)-training approach. From the empirical results, we find that SSDS training is computationally inexpensive (compared to PGD-training) while achieving comparable performances. SSDS training also helps robust models to maintain a relatively high level of performance for clean data as well as under black-box attacks.