A Saddle-Point Dynamical System Approach for Robust Deep Learning

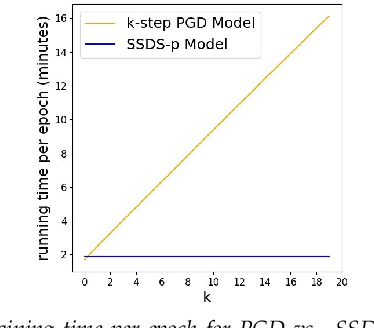
We propose a novel discrete-time dynamical system-based framework for achieving adversarial robustness in machine learning models. Our algorithm is originated from robust optimization, which aims to find the saddle point of a min-max optimization problem in the presence of uncertainties. The robust learning problem is formulated as a robust optimization problem, and we introduce a discrete-time algorithm based on a saddle-point dynamical system (SDS) to solve this problem. Under the assumptions that the cost function is convex and uncertainties enter concavely in the robust learning problem, we analytically show that using a diminishing step-size, the stochastic version of our algorithm, SSDS converges asymptotically to the robust optimal solution. The algorithm is deployed for the training of adversarially robust deep neural networks. Although such training involves highly non-convex non-concave robust optimization problems, empirical results show that the algorithm can achieve significant robustness for deep learning. We compare the performance of our SSDS model to other state-of-the-art robust models, e.g., trained using the projected gradient descent (PGD)-training approach. From the empirical results, we find that SSDS training is computationally inexpensive (compared to PGD-training) while achieving comparable performances. SSDS training also helps robust models to maintain a relatively high level of performance for clean data as well as under black-box attacks.

Particle Clustering Machine: A Dynamical System Based Approach

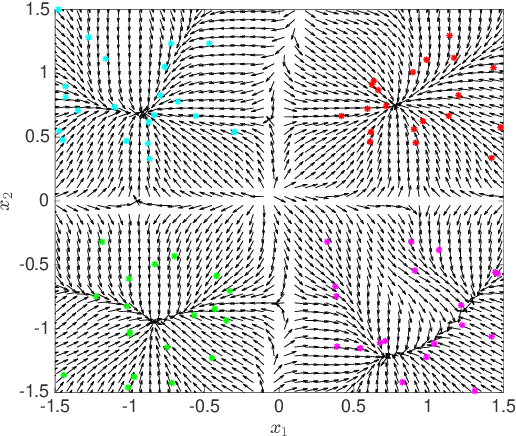
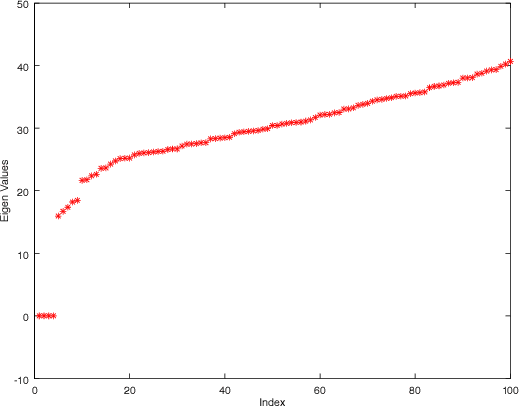
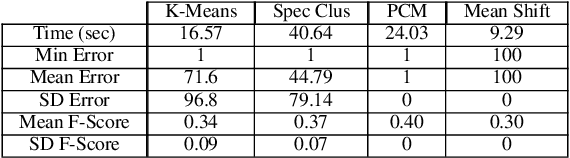
Identification of the clusters from an unlabeled data set is one of the most important problems in Unsupervised Machine Learning. The state of the art clustering algorithms are based on either the statistical properties or the geometric properties of the data set. In this work, we propose a novel method to cluster the data points using dynamical systems theory. After constructing a gradient dynamical system using interaction potential, we prove that the asymptotic dynamics of this system will determine the cluster centers, when the dynamical system is initialized at the data points. Most of the existing heuristic-based clustering techniques suffer from a disadvantage, namely the stochastic nature of the solution. Whereas, the proposed algorithm is deterministic, and the outcome would not change over multiple runs of the proposed algorithm with the same input data. Another advantage of the proposed method is that the number of clusters, which is difficult to determine in practice, does not have to be specified in advance. Simulation results with are presented, and comparisons are made with the existing methods.