Understanding A Class of Decentralized and Federated Optimization Algorithms: A Multi-Rate Feedback Control Perspective

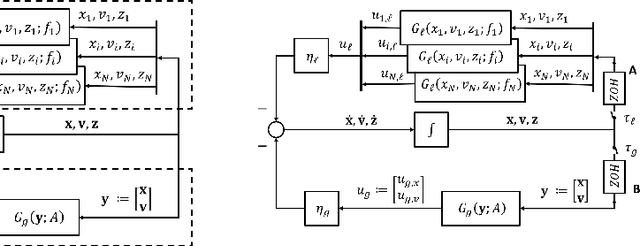
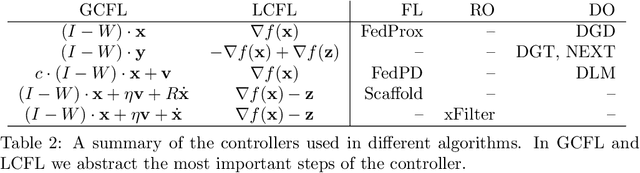
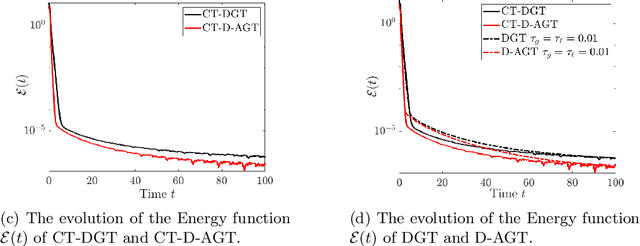
Distributed algorithms have been playing an increasingly important role in many applications such as machine learning, signal processing, and control. Significant research efforts have been devoted to developing and analyzing new algorithms for various applications. In this work, we provide a fresh perspective to understand, analyze, and design distributed optimization algorithms. Through the lens of multi-rate feedback control, we show that a wide class of distributed algorithms, including popular decentralized/federated schemes, can be viewed as discretizing a certain continuous-time feedback control system, possibly with multiple sampling rates, such as decentralized gradient descent, gradient tracking, and federated averaging. This key observation not only allows us to develop a generic framework to analyze the convergence of the entire algorithm class. More importantly, it also leads to an interesting way of designing new distributed algorithms. We develop the theory behind our framework and provide examples to highlight how the framework can be used in practice.

A Saddle-Point Dynamical System Approach for Robust Deep Learning

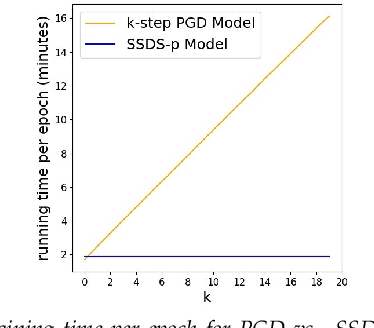
We propose a novel discrete-time dynamical system-based framework for achieving adversarial robustness in machine learning models. Our algorithm is originated from robust optimization, which aims to find the saddle point of a min-max optimization problem in the presence of uncertainties. The robust learning problem is formulated as a robust optimization problem, and we introduce a discrete-time algorithm based on a saddle-point dynamical system (SDS) to solve this problem. Under the assumptions that the cost function is convex and uncertainties enter concavely in the robust learning problem, we analytically show that using a diminishing step-size, the stochastic version of our algorithm, SSDS converges asymptotically to the robust optimal solution. The algorithm is deployed for the training of adversarially robust deep neural networks. Although such training involves highly non-convex non-concave robust optimization problems, empirical results show that the algorithm can achieve significant robustness for deep learning. We compare the performance of our SSDS model to other state-of-the-art robust models, e.g., trained using the projected gradient descent (PGD)-training approach. From the empirical results, we find that SSDS training is computationally inexpensive (compared to PGD-training) while achieving comparable performances. SSDS training also helps robust models to maintain a relatively high level of performance for clean data as well as under black-box attacks.