Particle Clustering Machine: A Dynamical System Based Approach
Paper and Code
Dec 30, 2017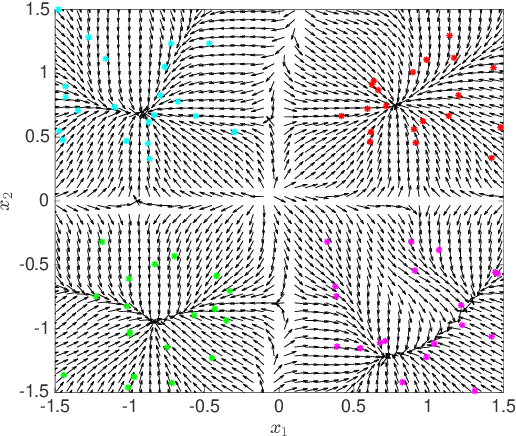

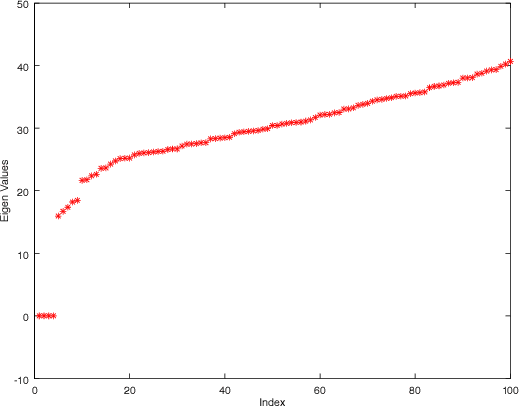
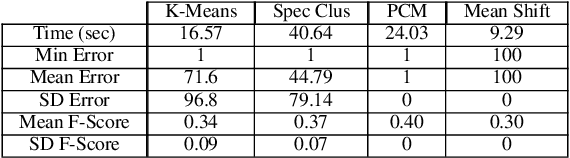
Identification of the clusters from an unlabeled data set is one of the most important problems in Unsupervised Machine Learning. The state of the art clustering algorithms are based on either the statistical properties or the geometric properties of the data set. In this work, we propose a novel method to cluster the data points using dynamical systems theory. After constructing a gradient dynamical system using interaction potential, we prove that the asymptotic dynamics of this system will determine the cluster centers, when the dynamical system is initialized at the data points. Most of the existing heuristic-based clustering techniques suffer from a disadvantage, namely the stochastic nature of the solution. Whereas, the proposed algorithm is deterministic, and the outcome would not change over multiple runs of the proposed algorithm with the same input data. Another advantage of the proposed method is that the number of clusters, which is difficult to determine in practice, does not have to be specified in advance. Simulation results with are presented, and comparisons are made with the existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge