Safe Navigation in Dynamic Environments using Density Functions

This work uses density functions for safe navigation in dynamic environments. The dynamic environment consists of time-varying obstacles as well as time-varying target sets. We propose an analytical construction of time-varying density functions to solve these navigation problems. The proposed approach leads to a time-varying feedback controller obtained as a positive gradient of the density function. This paper's main contribution is providing convergence proof using the analytically constructed density function for safe navigation in the presence of a dynamic obstacle set and time-varying target set. The results are the first of this kind developed for a system with integrator dynamics and open up the possibility for application to systems with more complex dynamics using methods based on control density function and inverse kinematic-based control design. We present the application of the developed approach for collision avoidance in multi-agent systems and robotic systems. While the theoretical results are produced for first-order integrator systems, we demonstrate how the framework can be applied for systems with non-trivial dynamics, such as Dubin's car model and fully actuated Euler-Lagrange system with robotics applications.

Off-Road Navigation of Legged Robots Using Linear Transfer Operators

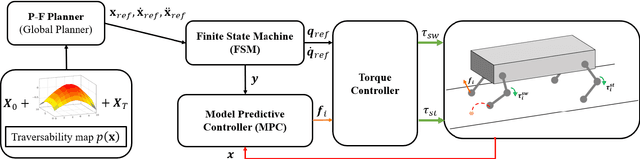
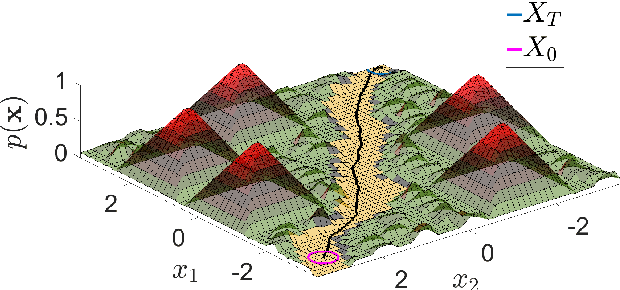
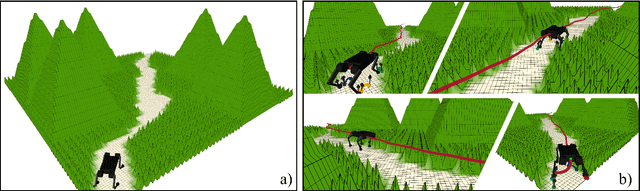
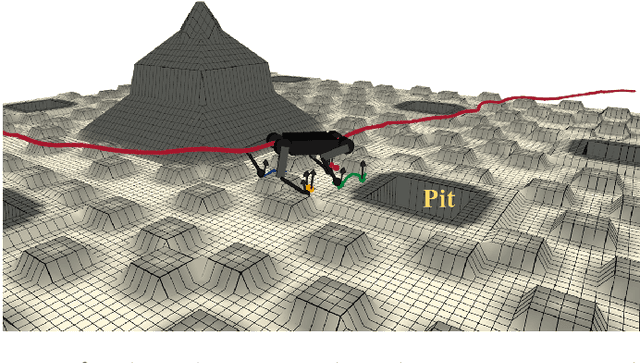
This paper presents the implementation of off-road navigation on legged robots using convex optimization through linear transfer operators. Given a traversability measure that captures the off-road environment, we lift the navigation problem into the density space using the Perron-Frobenius (P-F) operator. This allows the problem formulation to be represented as a convex optimization. Due to the operator acting on an infinite-dimensional density space, we use data collected from the terrain to get a finite-dimension approximation of the convex optimization. Results of the optimal trajectory for off-road navigation are compared with a standard iterative planner, where we show how our convex optimization generates a more traversable path for the legged robot compared to the suboptimal iterative planner.