Safety using Analytically Constructed Density Functions

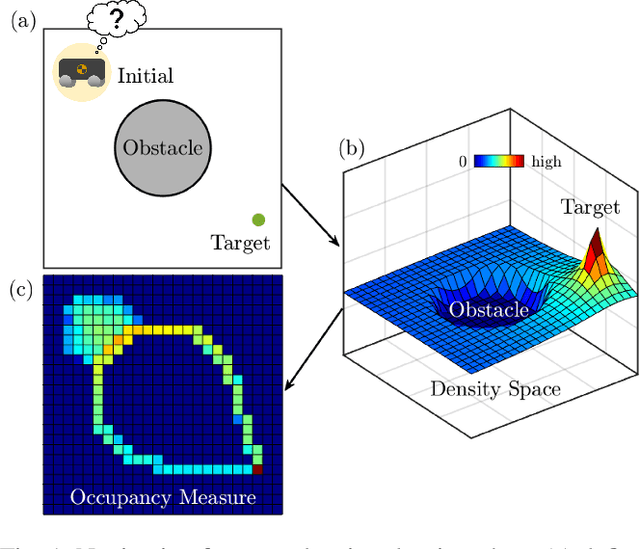
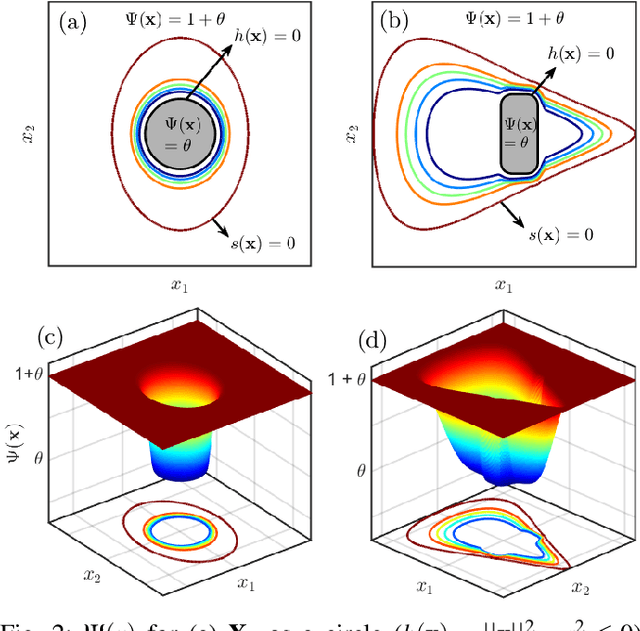
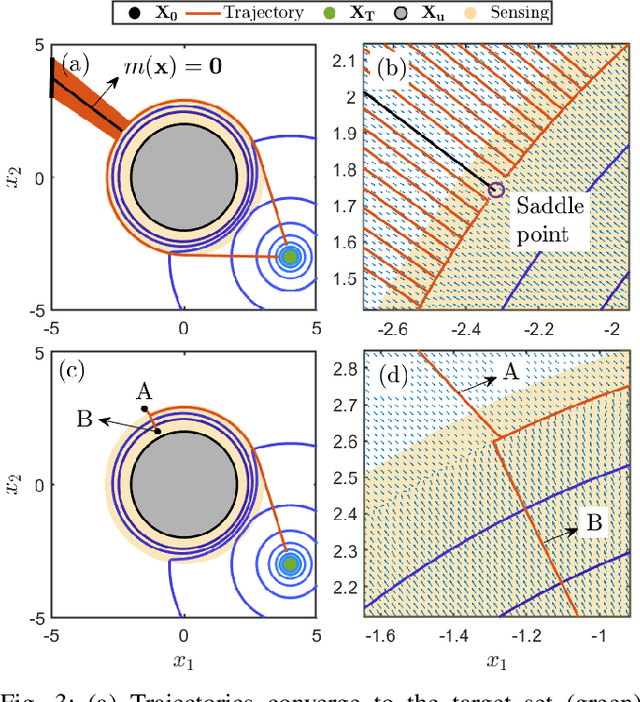
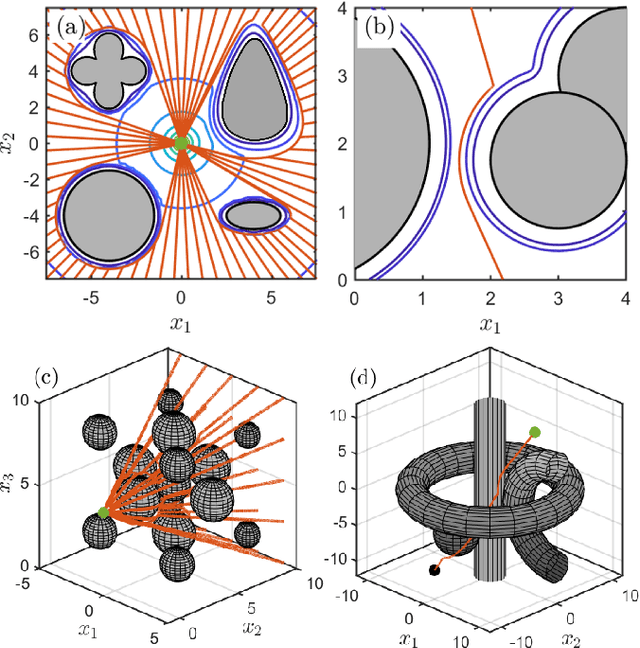
This paper presents a novel approach for safe control synthesis using the dual formulation of the navigation problem. The main contribution of this paper is in the analytical construction of density functions for almost everywhere navigation with safety constraints. In contrast to the existing approaches, where density functions are used for the analysis of navigation problems, we use density functions for the synthesis of safe controllers. We provide convergence proof using the proposed density functions for navigation with safety. Further, we use these density functions to design feedback controllers capable of navigating in cluttered environments and high-dimensional configuration spaces. The proposed analytical construction of density functions overcomes the problem associated with navigation functions, which are known to exist but challenging to construct, and potential functions, which suffer from local minima. Application of the developed framework is demonstrated on simple integrator dynamics and fully actuated robotic systems.

SE Koopman-MPC: Data-driven Learning and Control of Quadrotor UAVs

In this paper, we propose a novel data-driven approach for learning and control of quadrotor UAVs based on the Koopman operator and extended dynamic mode decomposition (EDMD). Building observables for EDMD based on conventional methods like Euler angles or quaternions to represent orientation is known to involve singularities. To address this issue, we employ a set of physics-informed observables based on the underlying topology of the nonlinear system. We use rotation matrices to directly represent the orientation dynamics and obtain a lifted linear representation of the nonlinear quadrotor dynamics in the SE(3) manifold. This EDMD model leads to accurate prediction and can generalize to several validation sets. Further, we design a linear model predictive controller (MPC) based on the proposed EDMD model to track agile reference trajectories. Simulation results show that the proposed MPC controller can run as fast as 100 Hz and is able to track arbitrary reference trajectories with good accuracy. Implementation details can be found in \url{https://github.com/sriram-2502/KoopmanMPC_Quadrotor}