A convex data-driven approach for nonlinear control synthesis
Paper and Code
Jun 28, 2020
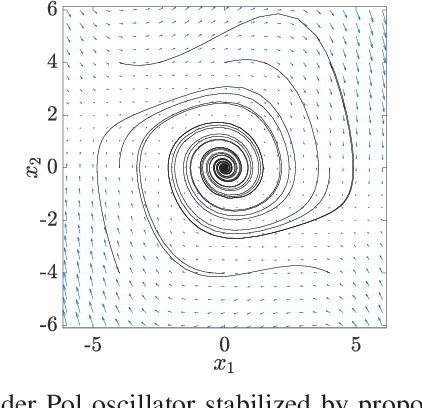
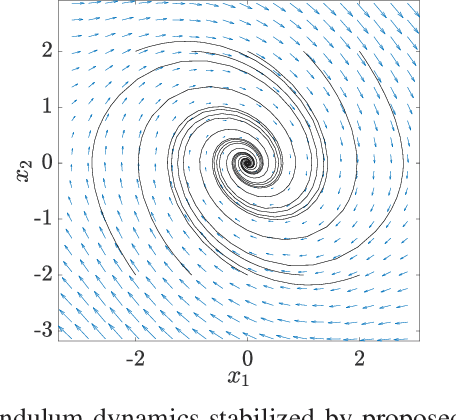
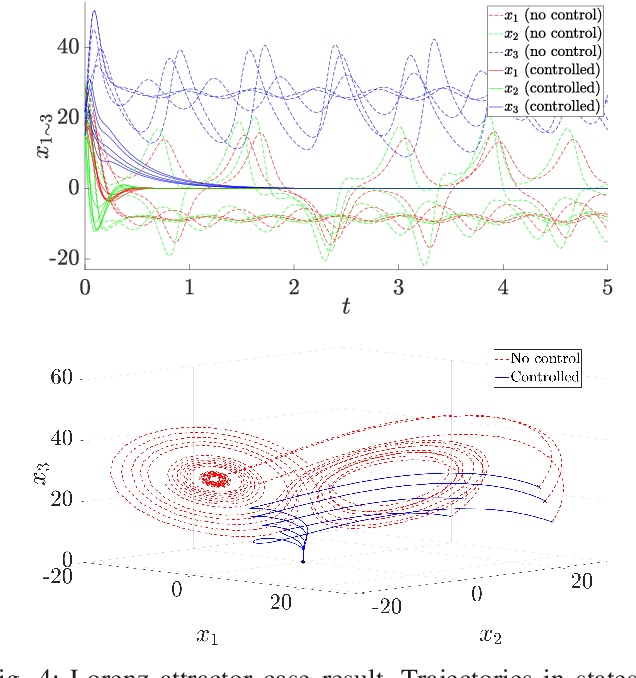
We consider a class of nonlinear control synthesis problems where the underlying mathematical models are not explicitly known. We propose a data-driven approach to stabilize the systems when only sample trajectories of the dynamics are accessible. Our method is founded on the density function based almost everywhere stability certificate that is dual to the Lyapunov function for dynamic systems. Unlike Lyapunov based methods, density functions lead to a convex formulation for a joint search of the control strategy and the stability certificate. This type of convex problem can be solved efficiently by invoking the machinery of the sum of squares (SOS). For the data-driven part, we exploit the fact that the duality results in the stability theory of the dynamical system can be understood using linear Perron-Frobenius and Koopman operators. This connection allows us to use data-driven methods developed to approximate these operators combined with the SOS techniques for the convex formulation of control synthesis. The efficacy of the proposed approach is demonstrated through several examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge