Yongxin Chen
Compositional Diffusion with Guided Search for Long-Horizon Planning
Jan 05, 2026Abstract:Generative models have emerged as powerful tools for planning, with compositional approaches offering particular promise for modeling long-horizon task distributions by composing together local, modular generative models. This compositional paradigm spans diverse domains, from multi-step manipulation planning to panoramic image synthesis to long video generation. However, compositional generative models face a critical challenge: when local distributions are multimodal, existing composition methods average incompatible modes, producing plans that are neither locally feasible nor globally coherent. We propose Compositional Diffusion with Guided Search (CDGS), which addresses this mode averaging problem by embedding search directly within the diffusion denoising process. Our method explores diverse combinations of local modes through population-based sampling, prunes infeasible candidates using likelihood-based filtering, and enforces global consistency through iterative resampling between overlapping segments. CDGS matches oracle performance on seven robot manipulation tasks, outperforming baselines that lack compositionality or require long-horizon training data. The approach generalizes across domains, enabling coherent text-guided panoramic images and long videos through effective local-to-global message passing. More details: https://cdgsearch.github.io/
CETCAM: Camera-Controllable Video Generation via Consistent and Extensible Tokenization
Dec 22, 2025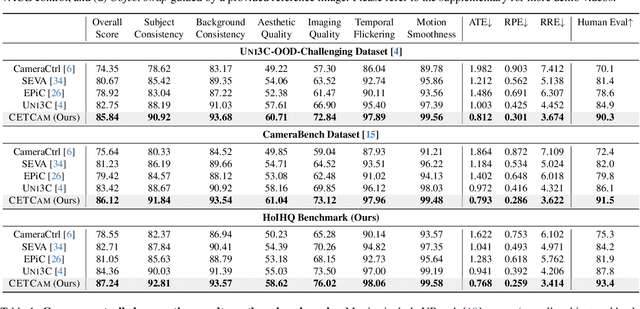
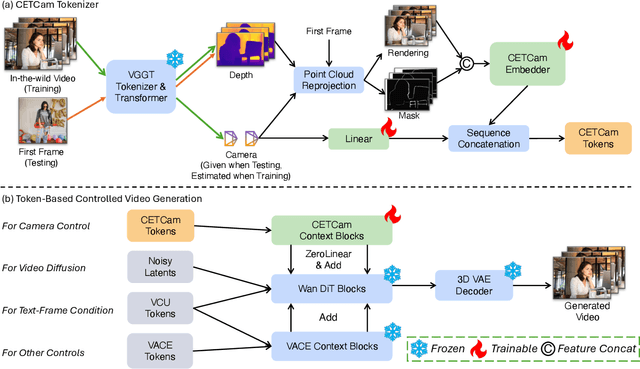
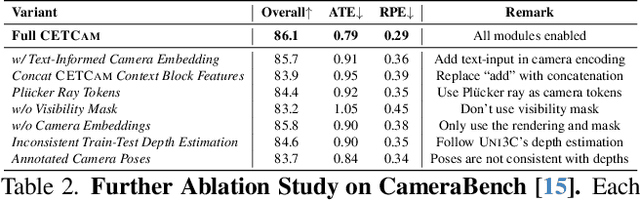

Abstract:Achieving precise camera control in video generation remains challenging, as existing methods often rely on camera pose annotations that are difficult to scale to large and dynamic datasets and are frequently inconsistent with depth estimation, leading to train-test discrepancies. We introduce CETCAM, a camera-controllable video generation framework that eliminates the need for camera annotations through a consistent and extensible tokenization scheme. CETCAM leverages recent advances in geometry foundation models, such as VGGT, to estimate depth and camera parameters and converts them into unified, geometry-aware tokens. These tokens are seamlessly integrated into a pretrained video diffusion backbone via lightweight context blocks. Trained in two progressive stages, CETCAM first learns robust camera controllability from diverse raw video data and then refines fine-grained visual quality using curated high-fidelity datasets. Extensive experiments across multiple benchmarks demonstrate state-of-the-art geometric consistency, temporal stability, and visual realism. Moreover, CETCAM exhibits strong adaptability to additional control modalities, including inpainting and layout control, highlighting its flexibility beyond camera control. The project page is available at https://sjtuytc.github.io/CETCam_project_page.github.io/.
Joint Model-based Model-free Diffusion for Planning with Constraints
Sep 10, 2025Abstract:Model-free diffusion planners have shown great promise for robot motion planning, but practical robotic systems often require combining them with model-based optimization modules to enforce constraints, such as safety. Naively integrating these modules presents compatibility challenges when diffusion's multi-modal outputs behave adversarially to optimization-based modules. To address this, we introduce Joint Model-based Model-free Diffusion (JM2D), a novel generative modeling framework. JM2D formulates module integration as a joint sampling problem to maximize compatibility via an interaction potential, without additional training. Using importance sampling, JM2D guides modules outputs based only on evaluations of the interaction potential, thus handling non-differentiable objectives commonly arising from non-convex optimization modules. We evaluate JM2D via application to aligning diffusion planners with safety modules on offline RL and robot manipulation. JM2D significantly improves task performance compared to conventional safety filters without sacrificing safety. Further, we show that conditional generation is a special case of JM2D and elucidate key design choices by comparing with SOTA gradient-based and projection-based diffusion planners. More details at: https://jm2d-corl25.github.io/.
Articulated Kinematics Distillation from Video Diffusion Models
Apr 01, 2025Abstract:We present Articulated Kinematics Distillation (AKD), a framework for generating high-fidelity character animations by merging the strengths of skeleton-based animation and modern generative models. AKD uses a skeleton-based representation for rigged 3D assets, drastically reducing the Degrees of Freedom (DoFs) by focusing on joint-level control, which allows for efficient, consistent motion synthesis. Through Score Distillation Sampling (SDS) with pre-trained video diffusion models, AKD distills complex, articulated motions while maintaining structural integrity, overcoming challenges faced by 4D neural deformation fields in preserving shape consistency. This approach is naturally compatible with physics-based simulation, ensuring physically plausible interactions. Experiments show that AKD achieves superior 3D consistency and motion quality compared with existing works on text-to-4D generation. Project page: https://research.nvidia.com/labs/dir/akd/
Direct Discriminative Optimization: Your Likelihood-Based Visual Generative Model is Secretly a GAN Discriminator
Mar 03, 2025Abstract:While likelihood-based generative models, particularly diffusion and autoregressive models, have achieved remarkable fidelity in visual generation, the maximum likelihood estimation (MLE) objective inherently suffers from a mode-covering tendency that limits the generation quality under limited model capacity. In this work, we propose Direct Discriminative Optimization (DDO) as a unified framework that bridges likelihood-based generative training and the GAN objective to bypass this fundamental constraint. Our key insight is to parameterize a discriminator implicitly using the likelihood ratio between a learnable target model and a fixed reference model, drawing parallels with the philosophy of Direct Preference Optimization (DPO). Unlike GANs, this parameterization eliminates the need for joint training of generator and discriminator networks, allowing for direct, efficient, and effective finetuning of a well-trained model to its full potential beyond the limits of MLE. DDO can be performed iteratively in a self-play manner for progressive model refinement, with each round requiring less than 1% of pretraining epochs. Our experiments demonstrate the effectiveness of DDO by significantly advancing the previous SOTA diffusion model EDM, reducing FID scores from 1.79/1.58 to new records of 1.30/0.97 on CIFAR-10/ImageNet-64 datasets, and by consistently improving both guidance-free and CFG-enhanced FIDs of visual autoregressive models on ImageNet 256$\times$256.
Complexity Analysis of Normalizing Constant Estimation: from Jarzynski Equality to Annealed Importance Sampling and beyond
Feb 07, 2025Abstract:Given an unnormalized probability density $\pi\propto\mathrm{e}^{-V}$, estimating its normalizing constant $Z=\int_{\mathbb{R}^d}\mathrm{e}^{-V(x)}\mathrm{d}x$ or free energy $F=-\log Z$ is a crucial problem in Bayesian statistics, statistical mechanics, and machine learning. It is challenging especially in high dimensions or when $\pi$ is multimodal. To mitigate the high variance of conventional importance sampling estimators, annealing-based methods such as Jarzynski equality and annealed importance sampling are commonly adopted, yet their quantitative complexity guarantees remain largely unexplored. We take a first step toward a non-asymptotic analysis of annealed importance sampling. In particular, we derive an oracle complexity of $\widetilde{O}\left(\frac{d\beta^2{\mathcal{A}}^2}{\varepsilon^4}\right)$ for estimating $Z$ within $\varepsilon$ relative error with high probability, where $\beta$ is the smoothness of $V$ and $\mathcal{A}$ denotes the action of a curve of probability measures interpolating $\pi$ and a tractable reference distribution. Our analysis, leveraging Girsanov theorem and optimal transport, does not explicitly require isoperimetric assumptions on the target distribution. Finally, to tackle the large action of the widely used geometric interpolation of probability distributions, we propose a new normalizing constant estimation algorithm based on reverse diffusion samplers and establish a framework for analyzing its complexity.
Cosmos World Foundation Model Platform for Physical AI
Jan 07, 2025



Abstract:Physical AI needs to be trained digitally first. It needs a digital twin of itself, the policy model, and a digital twin of the world, the world model. In this paper, we present the Cosmos World Foundation Model Platform to help developers build customized world models for their Physical AI setups. We position a world foundation model as a general-purpose world model that can be fine-tuned into customized world models for downstream applications. Our platform covers a video curation pipeline, pre-trained world foundation models, examples of post-training of pre-trained world foundation models, and video tokenizers. To help Physical AI builders solve the most critical problems of our society, we make our platform open-source and our models open-weight with permissive licenses available via https://github.com/NVIDIA/Cosmos.
Accelerating Gaussian Variational Inference for Motion Planning Under Uncertainty
Nov 05, 2024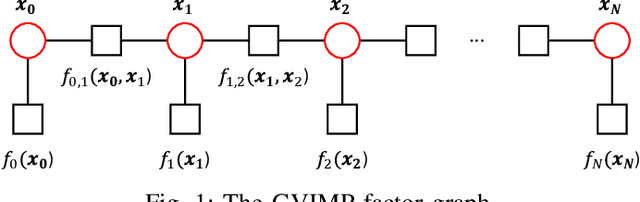
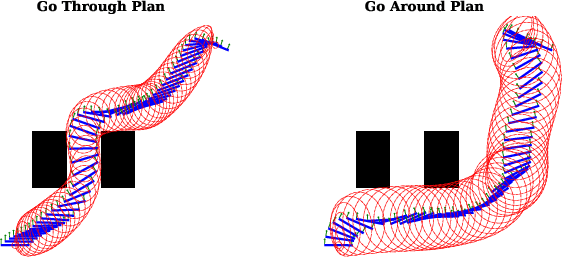
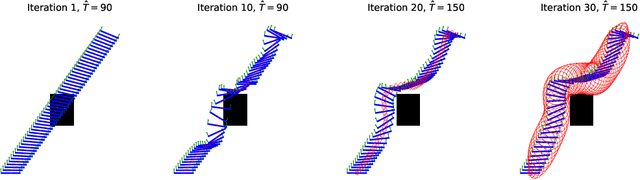
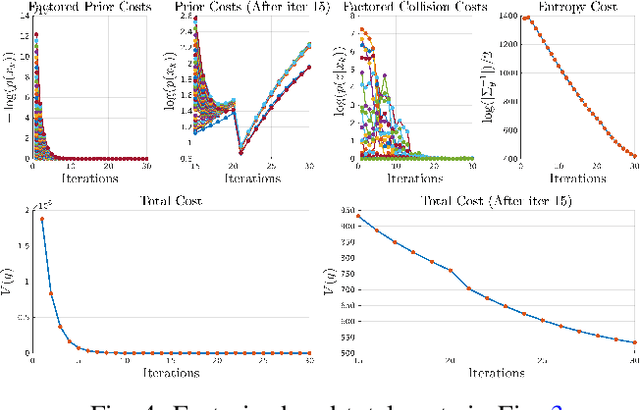
Abstract:This work addresses motion planning under uncertainty as a stochastic optimal control problem. The path distribution induced by the optimal controller corresponds to a posterior path distribution with a known form. To approximate this posterior, we frame an optimization problem in the space of Gaussian distributions, which aligns with the Gaussian Variational Inference Motion Planning (GVIMP) paradigm introduced in \cite{yu2023gaussian}. In this framework, the computation bottleneck lies in evaluating the expectation of collision costs over a dense discretized trajectory and computing the marginal covariances. This work exploits the sparse motion planning factor graph, which allows for parallel computing collision costs and Gaussian Belief Propagation (GBP) marginal covariance computation, to introduce a computationally efficient approach to solving GVIMP. We term the novel paradigm as the Parallel Gaussian Variational Inference Motion Planning (P-GVIMP). We validate the proposed framework on various robotic systems, demonstrating significant speed acceleration achieved by leveraging Graphics Processing Units (GPUs) for parallel computation. An open-sourced implementation is presented at https://github.com/hzyu17/VIMP.
Path Integral Control for Hybrid Dynamical Systems
Nov 01, 2024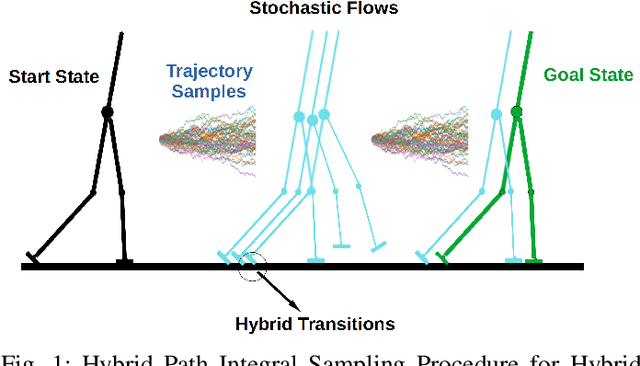
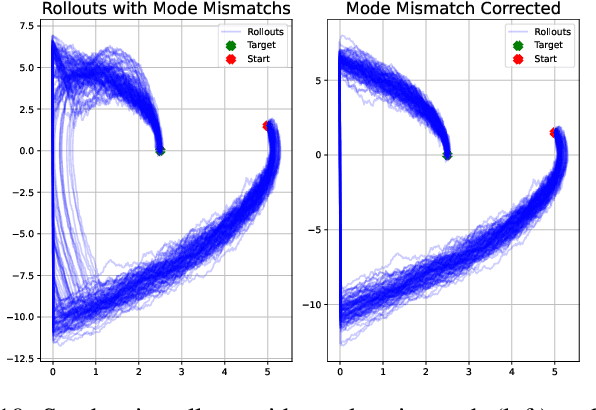
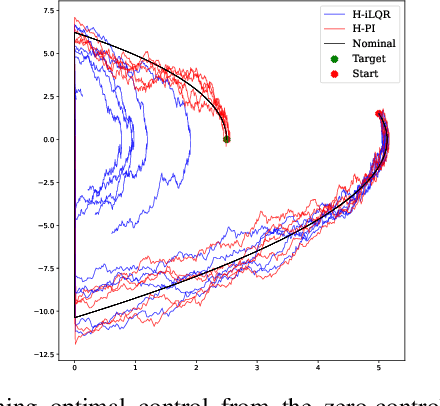
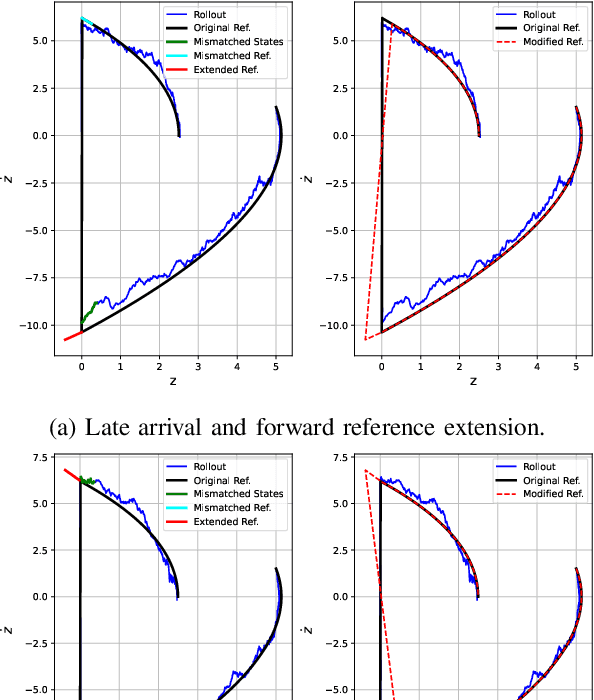
Abstract:This work introduces a novel paradigm for solving optimal control problems for hybrid dynamical systems under uncertainties. Robotic systems having contact with the environment can be modeled as hybrid systems. Controller design for hybrid systems under disturbances is complicated by the discontinuous jump dynamics, mode changes with inconsistent state dimensions, and variations in jumping timing and states caused by noise. We formulate this problem into a stochastic control problem with hybrid transition constraints and propose the Hybrid Path Integral (H-PI) framework to obtain the optimal controller. Despite random mode changes across stochastic path samples, we show that the ratio between hybrid path distributions with varying drift terms remains analogous to the smooth path distributions. We then show that the optimal controller can be obtained by evaluating a path integral with hybrid constraints. Importance sampling for path distributions with hybrid dynamics constraints is introduced to reduce the variance of the path integral evaluation, where we leverage the recently developed Hybrid iterative-Linear-Quadratic-Regulator (H-iLQR) controller to induce a hybrid path distribution proposal with low variance. The proposed method is validated through numerical experiments on various hybrid systems and extensive ablation studies. All the sampling processes are conducted in parallel on a Graphics Processing Unit (GPU).
Improving Neural Optimal Transport via Displacement Interpolation
Oct 03, 2024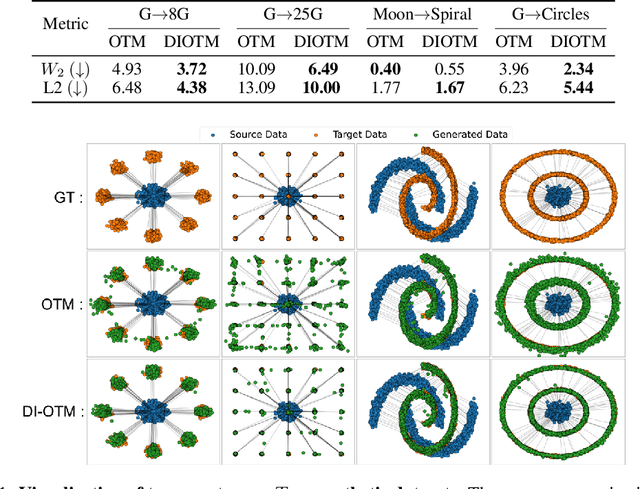

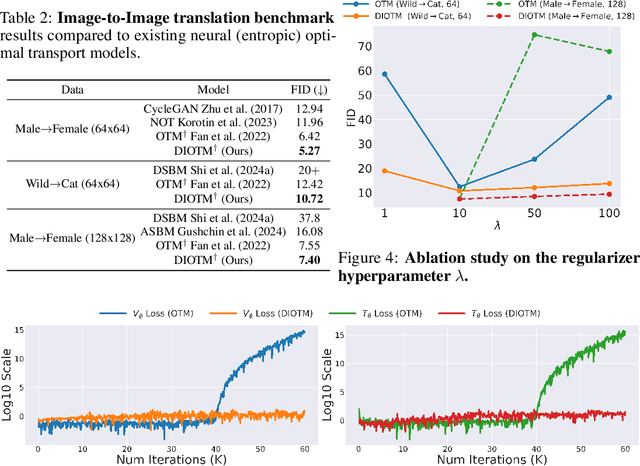

Abstract:Optimal Transport (OT) theory investigates the cost-minimizing transport map that moves a source distribution to a target distribution. Recently, several approaches have emerged for learning the optimal transport map for a given cost function using neural networks. We refer to these approaches as the OT Map. OT Map provides a powerful tool for diverse machine learning tasks, such as generative modeling and unpaired image-to-image translation. However, existing methods that utilize max-min optimization often experience training instability and sensitivity to hyperparameters. In this paper, we propose a novel method to improve stability and achieve a better approximation of the OT Map by exploiting displacement interpolation, dubbed Displacement Interpolation Optimal Transport Model (DIOTM). We derive the dual formulation of displacement interpolation at specific time $t$ and prove how these dual problems are related across time. This result allows us to utilize the entire trajectory of displacement interpolation in learning the OT Map. Our method improves the training stability and achieves superior results in estimating optimal transport maps. We demonstrate that DIOTM outperforms existing OT-based models on image-to-image translation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge