Accelerating Gaussian Variational Inference for Motion Planning Under Uncertainty

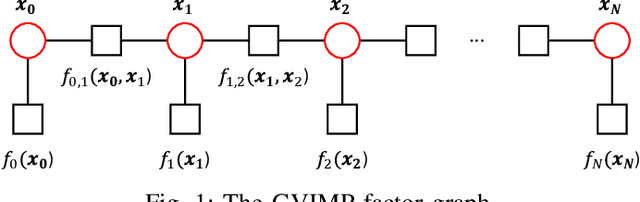
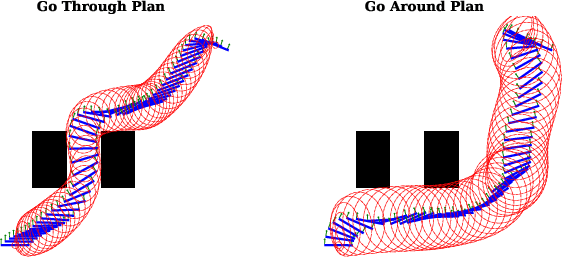
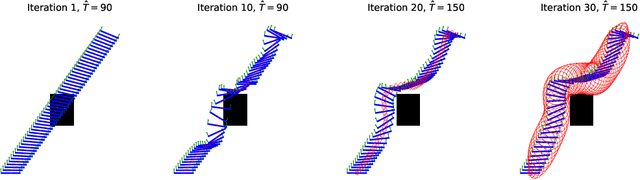
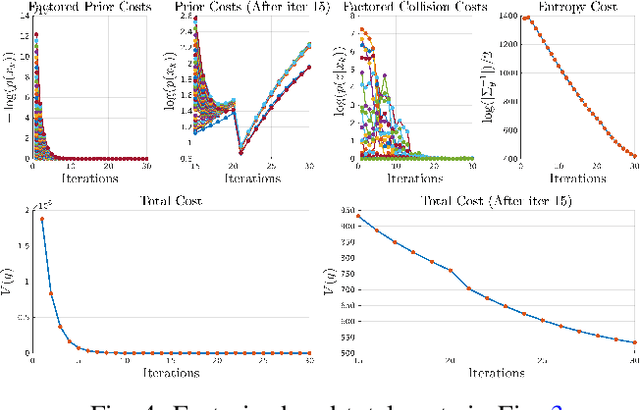
This work addresses motion planning under uncertainty as a stochastic optimal control problem. The path distribution induced by the optimal controller corresponds to a posterior path distribution with a known form. To approximate this posterior, we frame an optimization problem in the space of Gaussian distributions, which aligns with the Gaussian Variational Inference Motion Planning (GVIMP) paradigm introduced in \cite{yu2023gaussian}. In this framework, the computation bottleneck lies in evaluating the expectation of collision costs over a dense discretized trajectory and computing the marginal covariances. This work exploits the sparse motion planning factor graph, which allows for parallel computing collision costs and Gaussian Belief Propagation (GBP) marginal covariance computation, to introduce a computationally efficient approach to solving GVIMP. We term the novel paradigm as the Parallel Gaussian Variational Inference Motion Planning (P-GVIMP). We validate the proposed framework on various robotic systems, demonstrating significant speed acceleration achieved by leveraging Graphics Processing Units (GPUs) for parallel computation. An open-sourced implementation is presented at https://github.com/hzyu17/VIMP.

Path Integral Control for Hybrid Dynamical Systems

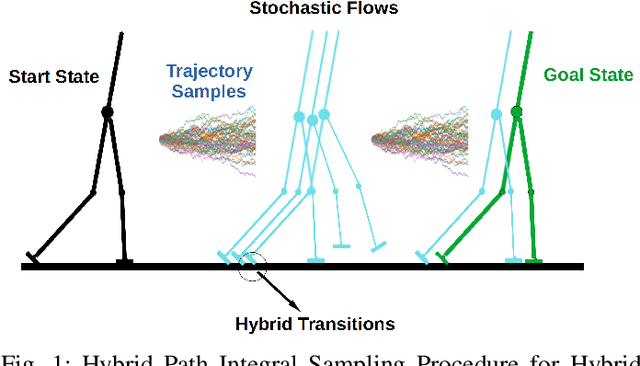
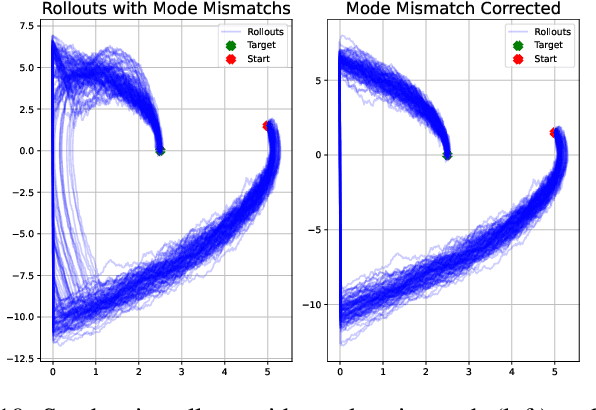
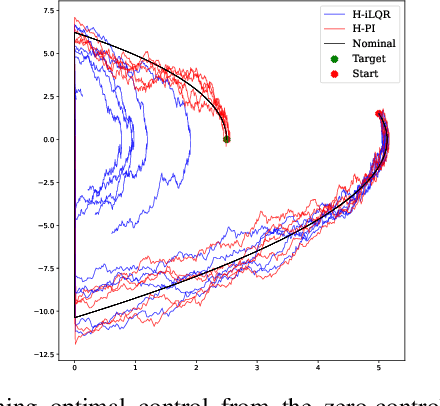
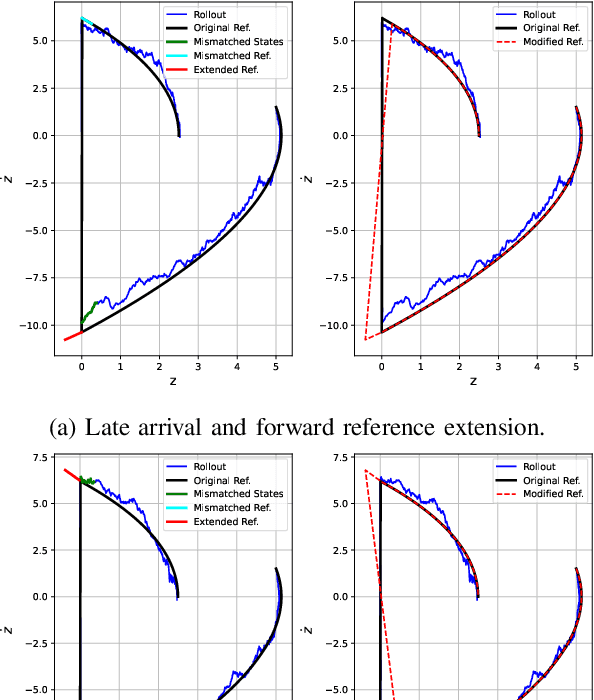
This work introduces a novel paradigm for solving optimal control problems for hybrid dynamical systems under uncertainties. Robotic systems having contact with the environment can be modeled as hybrid systems. Controller design for hybrid systems under disturbances is complicated by the discontinuous jump dynamics, mode changes with inconsistent state dimensions, and variations in jumping timing and states caused by noise. We formulate this problem into a stochastic control problem with hybrid transition constraints and propose the Hybrid Path Integral (H-PI) framework to obtain the optimal controller. Despite random mode changes across stochastic path samples, we show that the ratio between hybrid path distributions with varying drift terms remains analogous to the smooth path distributions. We then show that the optimal controller can be obtained by evaluating a path integral with hybrid constraints. Importance sampling for path distributions with hybrid dynamics constraints is introduced to reduce the variance of the path integral evaluation, where we leverage the recently developed Hybrid iterative-Linear-Quadratic-Regulator (H-iLQR) controller to induce a hybrid path distribution proposal with low variance. The proposed method is validated through numerical experiments on various hybrid systems and extensive ablation studies. All the sampling processes are conducted in parallel on a Graphics Processing Unit (GPU).

Efficient Belief Road Map for Planning Under Uncertainty

Robotic systems, particularly in demanding environments like narrow corridors or disaster zones, often grapple with imperfect state estimation. Addressing this challenge requires a trajectory plan that not only navigates these restrictive spaces but also manages the inherent uncertainty of the system. We present a novel approach for graph-based belief space planning via the use of an efficient covariance control algorithm. By adaptively steering state statistics via output state feedback, we efficiently craft a belief roadmap characterized by nodes with controlled uncertainty and edges representing collision-free mean trajectories. The roadmap's structured design then paves the way for precise path searches that balance control costs and uncertainty considerations. Our numerical experiments affirm the efficacy and advantage of our method in different motion planning tasks. Our open-source implementation can be found at https://github.com/hzyu17/VIMP/tree/BRM.

Stochastic Motion Planning as Gaussian Variational Inference: Theory and Algorithms

We consider the motion planning problem under uncertainty and address it using probabilistic inference. A collision-free motion plan with linear stochastic dynamics is modeled by a posterior distribution. Gaussian variational inference is an optimization over the path distributions to infer this posterior within the scope of Gaussian distributions. We propose Gaussian Variational Inference Motion Planner (GVI-MP) algorithm to solve this Gaussian inference, where a natural gradient paradigm is used to iteratively update the Gaussian distribution, and the factorized structure of the joint distribution is leveraged. We show that the direct optimization over the state distributions in GVI-MP is equivalent to solving a stochastic control that has a closed-form solution. Starting from this observation, we propose our second algorithm, Proximal Gradient Covariance Steering Motion Planner (PGCS-MP), to solve the same inference problem in its stochastic control form with terminal constraints. We use a proximal gradient paradigm to solve the linear stochastic control with nonlinear collision cost, where the nonlinear cost is iteratively approximated using quadratic functions and a closed-form solution can be obtained by solving a linear covariance steering at each iteration. We evaluate the effectiveness and the performance of the proposed approaches through extensive experiments on various robot models. The code for this paper can be found in https://github.com/hzyu17/VIMP.

A Gaussian variational inference approach to motion planning

We propose a Gaussian variational inference framework for the motion planning problem. In this framework, motion planning is formulated as an optimization over the distribution of the trajectories to approximate the desired trajectory distribution by a tractable Gaussian distribution. Equivalently, the proposed framework can be viewed as a standard motion planning with an entropy regularization. Thus, the solution obtained is a transition from an optimal deterministic solution to a stochastic one, and the proposed framework can recover the deterministic solution by controlling the level of stochasticity. To solve this optimization, we adopt the natural gradient descent scheme. The sparsity structure of the proposed formulation induced by factorized objective functions is further leveraged to improve the scalability of the algorithm. We evaluate our method on several robot systems in simulated environments, and show that it achieves collision avoidance with smooth trajectories, and meanwhile brings robustness to the deterministic baseline results, especially in challenging environments and tasks.

Learning to Navigate from Simulation via Spatial and Semantic Information Synthesis with Noise Model Embedding

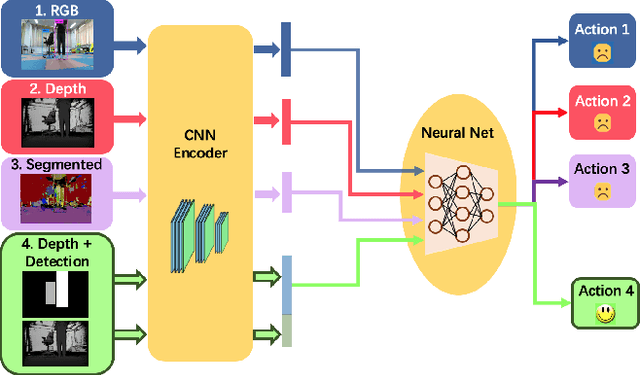
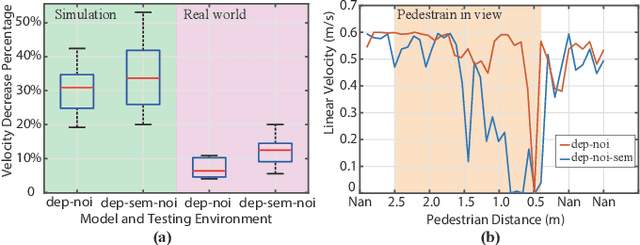
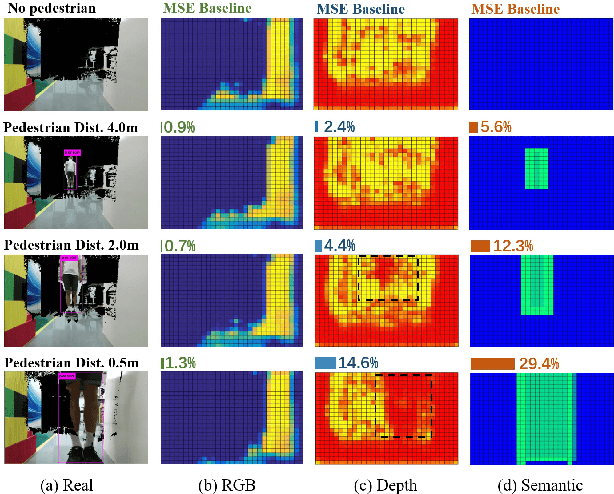
While training an end-to-end navigation network in the real world is usually of high cost, simulation provides a safe and cheap environment in this training stage. However, training neural network models in simulation brings up the problem of how to effectively transfer the model from simulation to the real world (sim-to-real). In this work, we regard the environment representation as a crucial element in this transfer process and propose a visual information pyramid (VIP) model to systematically investigate a practical environment representation. A novel representation composed of spatial and semantic information synthesis is then established accordingly, where noise model embedding is particularly considered. To explore the effectiveness of this representation, we compared the performance with representations popularly used in the literature in both simulated and real-world scenarios. Results suggest that our environment representation stands out. Furthermore, an analysis on the feature map is implemented to investigate the effectiveness through inner reaction, which could be irradiative for future researches on end-to-end navigation.