Path Integral Control for Hybrid Dynamical Systems

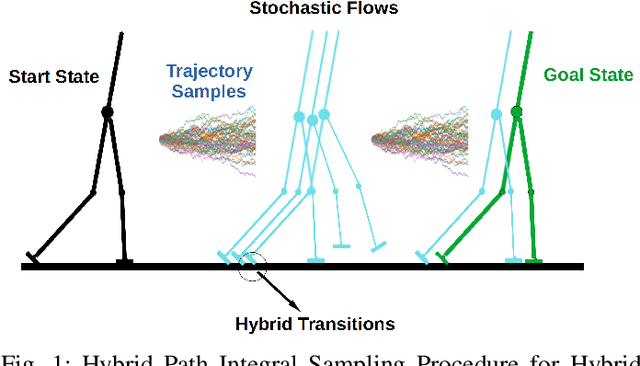
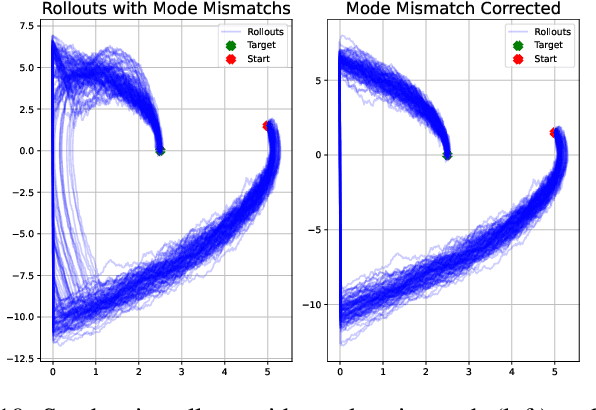
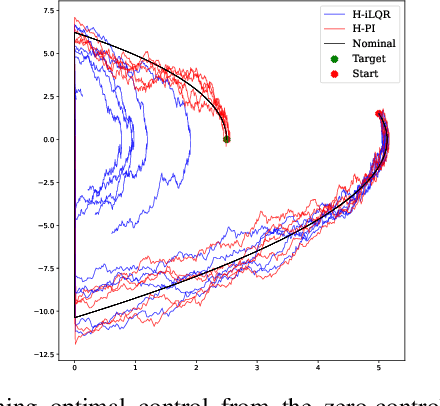
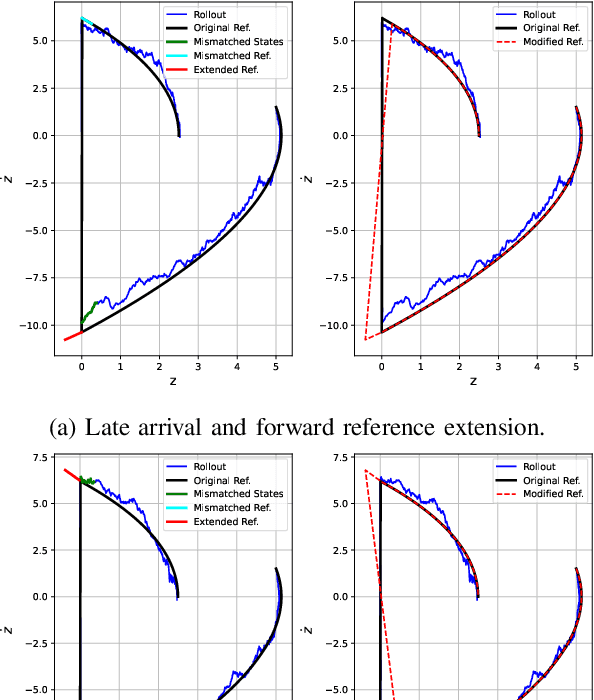
This work introduces a novel paradigm for solving optimal control problems for hybrid dynamical systems under uncertainties. Robotic systems having contact with the environment can be modeled as hybrid systems. Controller design for hybrid systems under disturbances is complicated by the discontinuous jump dynamics, mode changes with inconsistent state dimensions, and variations in jumping timing and states caused by noise. We formulate this problem into a stochastic control problem with hybrid transition constraints and propose the Hybrid Path Integral (H-PI) framework to obtain the optimal controller. Despite random mode changes across stochastic path samples, we show that the ratio between hybrid path distributions with varying drift terms remains analogous to the smooth path distributions. We then show that the optimal controller can be obtained by evaluating a path integral with hybrid constraints. Importance sampling for path distributions with hybrid dynamics constraints is introduced to reduce the variance of the path integral evaluation, where we leverage the recently developed Hybrid iterative-Linear-Quadratic-Regulator (H-iLQR) controller to induce a hybrid path distribution proposal with low variance. The proposed method is validated through numerical experiments on various hybrid systems and extensive ablation studies. All the sampling processes are conducted in parallel on a Graphics Processing Unit (GPU).