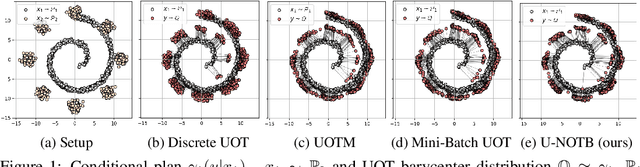
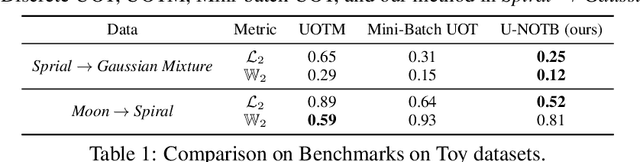
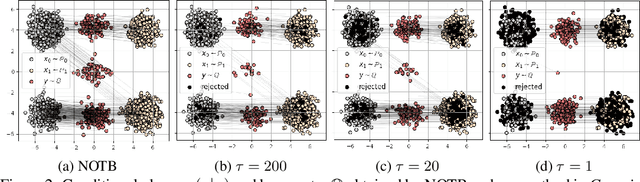
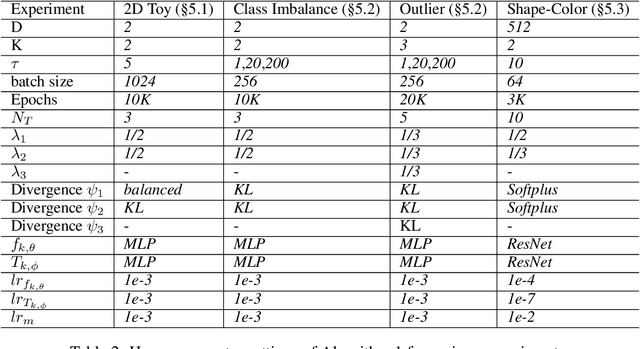
Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport

A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.

Improving Neural Optimal Transport via Displacement Interpolation

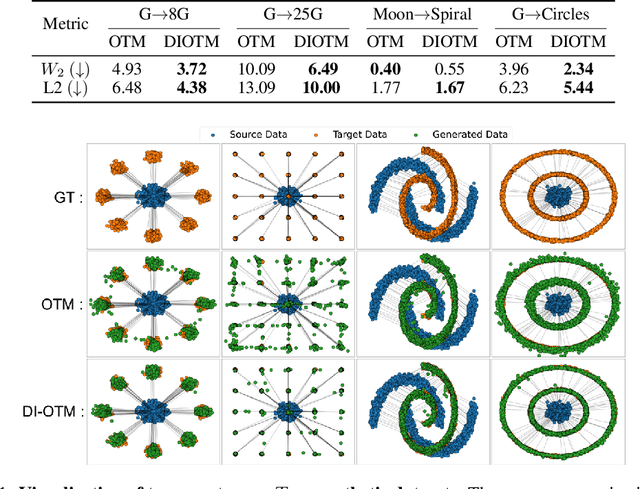
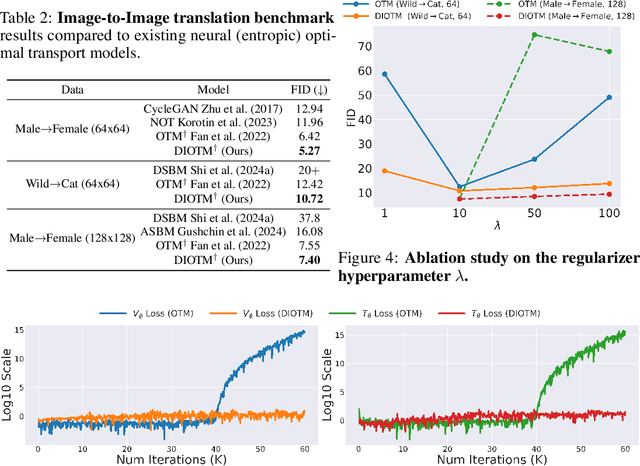
Optimal Transport (OT) theory investigates the cost-minimizing transport map that moves a source distribution to a target distribution. Recently, several approaches have emerged for learning the optimal transport map for a given cost function using neural networks. We refer to these approaches as the OT Map. OT Map provides a powerful tool for diverse machine learning tasks, such as generative modeling and unpaired image-to-image translation. However, existing methods that utilize max-min optimization often experience training instability and sensitivity to hyperparameters. In this paper, we propose a novel method to improve stability and achieve a better approximation of the OT Map by exploiting displacement interpolation, dubbed Displacement Interpolation Optimal Transport Model (DIOTM). We derive the dual formulation of displacement interpolation at specific time $t$ and prove how these dual problems are related across time. This result allows us to utilize the entire trajectory of displacement interpolation in learning the OT Map. Our method improves the training stability and achieves superior results in estimating optimal transport maps. We demonstrate that DIOTM outperforms existing OT-based models on image-to-image translation tasks.

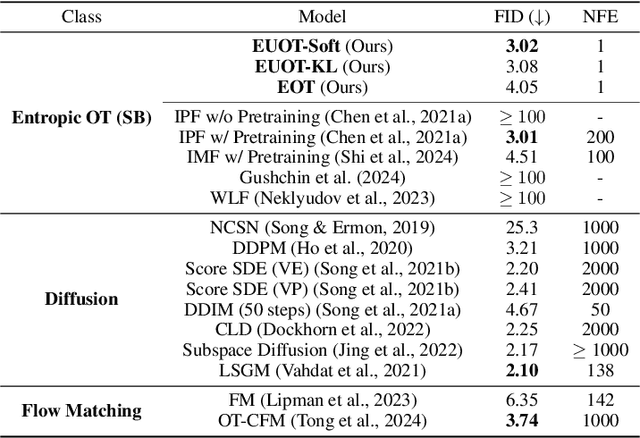
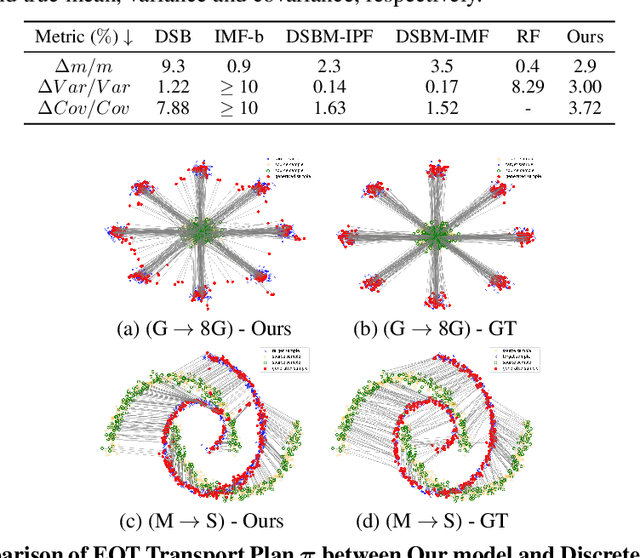
Scalable Simulation-free Entropic Unbalanced Optimal Transport

The Optimal Transport (OT) problem investigates a transport map that connects two distributions while minimizing a given cost function. Finding such a transport map has diverse applications in machine learning, such as generative modeling and image-to-image translation. In this paper, we introduce a scalable and simulation-free approach for solving the Entropic Unbalanced Optimal Transport (EUOT) problem. We derive the dynamical form of this EUOT problem, which is a generalization of the Schr\"odinger bridges (SB) problem. Based on this, we derive dual formulation and optimality conditions of the EUOT problem from the stochastic optimal control interpretation. By leveraging these properties, we propose a simulation-free algorithm to solve EUOT, called Simulation-free EUOT (SF-EUOT). While existing SB models require expensive simulation costs during training and evaluation, our model achieves simulation-free training and one-step generation by utilizing the reciprocal property. Our model demonstrates significantly improved scalability in generative modeling and image-to-image translation tasks compared to previous SB methods.

Unsupervised Point Cloud Completion through Unbalanced Optimal Transport

Unpaired point cloud completion explores methods for learning a completion map from unpaired incomplete and complete point cloud data. In this paper, we propose a novel approach for unpaired point cloud completion using the unbalanced optimal transport map, called Unbalanced Optimal Transport Map for Unpaired Point Cloud Completion (UOT-UPC). We demonstrate that the unpaired point cloud completion can be naturally interpreted as the Optimal Transport (OT) problem and introduce the Unbalanced Optimal Transport (UOT) approach to address the class imbalance problem, which is prevalent in unpaired point cloud completion datasets. Moreover, we analyze the appropriate cost function for unpaired completion tasks. This analysis shows that the InfoCD cost function is particularly well-suited for this task. Our model is the first attempt to leverage UOT for unpaired point cloud completion, achieving competitive or superior results on both single-category and multi-category datasets. In particular, our model is especially effective in scenarios with class imbalance, where the proportions of categories are different between the incomplete and complete point cloud datasets.

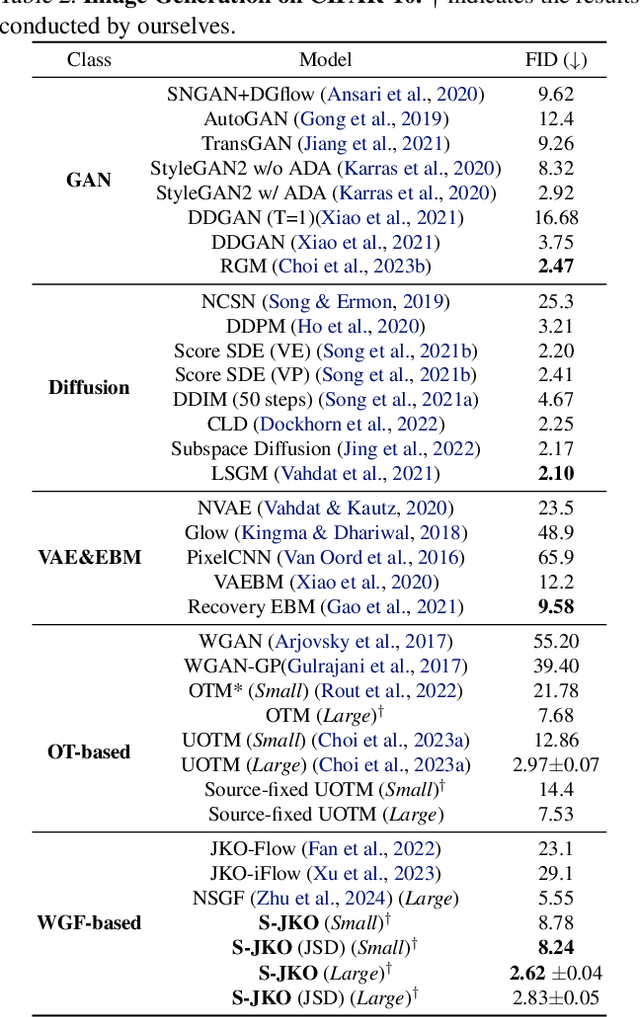
Scalable Wasserstein Gradient Flow for Generative Modeling through Unbalanced Optimal Transport

Wasserstein Gradient Flow (WGF) describes the gradient dynamics of probability density within the Wasserstein space. WGF provides a promising approach for conducting optimization over the probability distributions. Numerically approximating the continuous WGF requires the time discretization method. The most well-known method for this is the JKO scheme. In this regard, previous WGF models employ the JKO scheme and parametrize transport map for each JKO step. However, this approach results in quadratic training complexity $O(K^2)$ with the number of JKO step $K$. This severely limits the scalability of WGF models. In this paper, we introduce a scalable WGF-based generative model, called Semi-dual JKO (S-JKO). Our model is based on the semi-dual form of the JKO step, derived from the equivalence between the JKO step and the Unbalanced Optimal Transport. Our approach reduces the training complexity to $O(K)$. We demonstrate that our model significantly outperforms existing WGF-based generative models, achieving FID scores of 2.62 on CIFAR-10 and 6.19 on CelebA-HQ-256, which are comparable to state-of-the-art image generative models.

Analyzing and Improving OT-based Adversarial Networks

Optimal Transport (OT) problem aims to find a transport plan that bridges two distributions while minimizing a given cost function. OT theory has been widely utilized in generative modeling. In the beginning, OT distance has been used as a measure for assessing the distance between data and generated distributions. Recently, OT transport map between data and prior distributions has been utilized as a generative model. These OT-based generative models share a similar adversarial training objective. In this paper, we begin by unifying these OT-based adversarial methods within a single framework. Then, we elucidate the role of each component in training dynamics through a comprehensive analysis of this unified framework. Moreover, we suggest a simple but novel method that improves the previously best-performing OT-based model. Intuitively, our approach conducts a gradual refinement of the generated distribution, progressively aligning it with the data distribution. Our approach achieves a FID score of 2.51 on CIFAR-10, outperforming unified OT-based adversarial approaches.

Generative Modeling through the Semi-dual Formulation of Unbalanced Optimal Transport

Optimal Transport (OT) problem investigates a transport map that bridges two distributions while minimizing a given cost function. In this regard, OT between tractable prior distribution and data has been utilized for generative modeling tasks. However, OT-based methods are susceptible to outliers and face optimization challenges during training. In this paper, we propose a novel generative model based on the semi-dual formulation of Unbalanced Optimal Transport (UOT). Unlike OT, UOT relaxes the hard constraint on distribution matching. This approach provides better robustness against outliers, stability during training, and faster convergence. We validate these properties empirically through experiments. Moreover, we study the theoretical upper-bound of divergence between distributions in UOT. Our model outperforms existing OT-based generative models, achieving FID scores of 2.97 on CIFAR-10 and 5.80 on CelebA-HQ-256.

Restoration based Generative Models

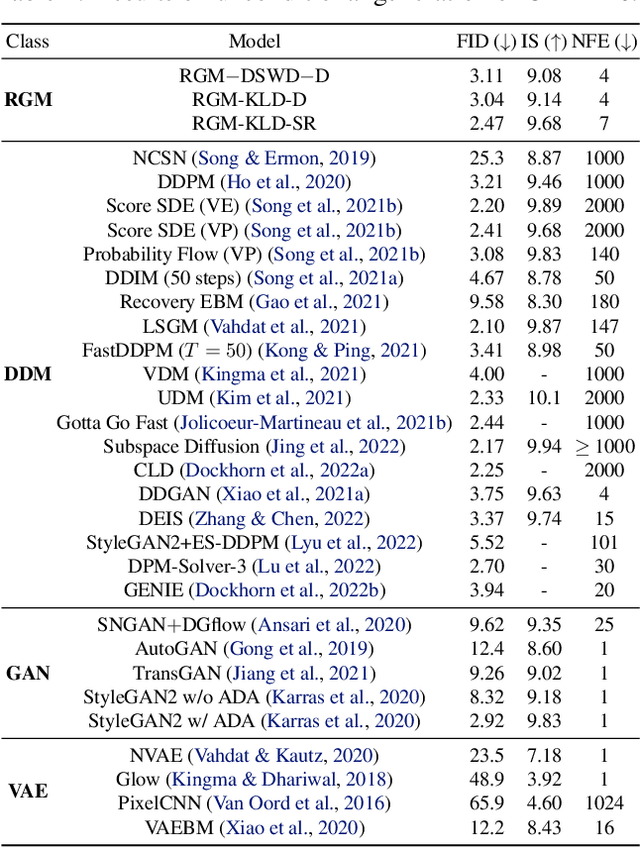
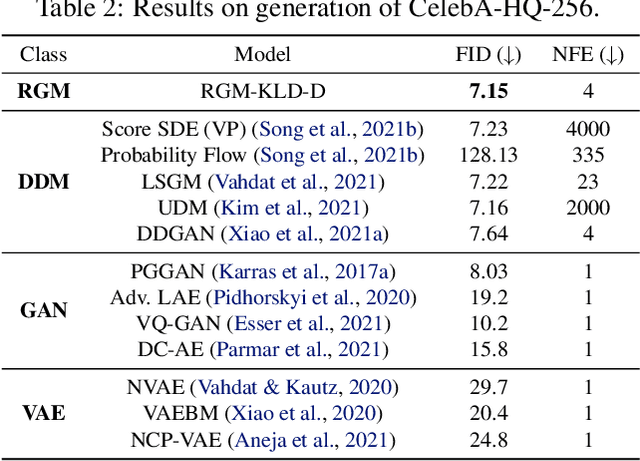
Denoising diffusion models (DDMs) have recently attracted increasing attention by showing impressive synthesis quality. DDMs are built on a diffusion process that pushes data to the noise distribution and the models learn to denoise. In this paper, we establish the interpretation of DDMs in terms of image restoration (IR). Integrating IR literature allows us to use an alternative objective and diverse forward processes, not confining to the diffusion process. By imposing prior knowledge on the loss function grounded on MAP-based estimation, we eliminate the need for the expensive sampling of DDMs. Also, we propose a multi-scale training, which improves the performance compared to the diffusion process, by taking advantage of the flexibility of the forward process. Experimental results demonstrate that our model improves the quality and efficiency of both training and inference. Furthermore, we show the applicability of our model to inverse problems. We believe that our framework paves the way for designing a new type of flexible general generative model.

Learning PDE Solution Operator for Continuous Modeling of Time-Series

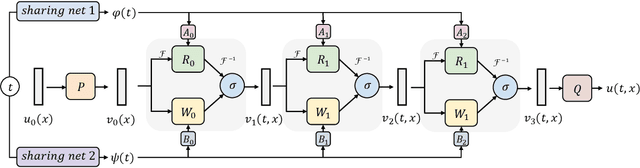
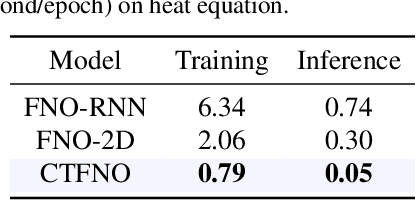
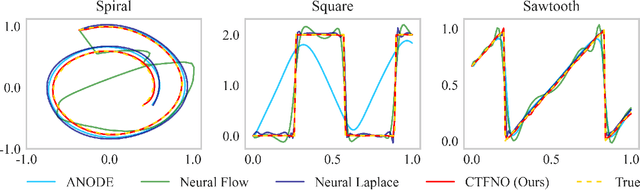
Learning underlying dynamics from data is important and challenging in many real-world scenarios. Incorporating differential equations (DEs) to design continuous networks has drawn much attention recently, however, most prior works make specific assumptions on the type of DEs, making the model specialized for particular problems. This work presents a partial differential equation (PDE) based framework which improves the dynamics modeling capability. Building upon the recent Fourier neural operator, we propose a neural operator that can handle time continuously without requiring iterative operations or specific grids of temporal discretization. A theoretical result demonstrating its universality is provided. We also uncover an intrinsic property of neural operators that improves data efficiency and model generalization by ensuring stability. Our model achieves superior accuracy in dealing with time-dependent PDEs compared to existing models. Furthermore, several numerical pieces of evidence validate that our method better represents a wide range of dynamics and outperforms state-of-the-art DE-based models in real-time-series applications. Our framework opens up a new way for a continuous representation of neural networks that can be readily adopted for real-world applications.

Robust Out-of-Distribution Detection on Deep Probabilistic Generative Models

Out-of-distribution (OOD) detection is an important task in machine learning systems for ensuring their reliability and safety. Deep probabilistic generative models facilitate OOD detection by estimating the likelihood of a data sample. However, such models frequently assign a suspiciously high likelihood to a specific outlier. Several recent works have addressed this issue by training a neural network with auxiliary outliers, which are generated by perturbing the input data. In this paper, we discover that these approaches fail for certain OOD datasets. Thus, we suggest a new detection metric that operates without outlier exposure. We observe that our metric is robust to diverse variations of an image compared to the previous outlier-exposing methods. Furthermore, our proposed score requires neither auxiliary models nor additional training. Instead, this paper utilizes the likelihood ratio statistic in a new perspective to extract genuine properties from the given single deep probabilistic generative model. We also apply a novel numerical approximation to enable fast implementation. Finally, we demonstrate comprehensive experiments on various probabilistic generative models and show that our method achieves state-of-the-art performance.