Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport
Paper and Code
Oct 04, 2024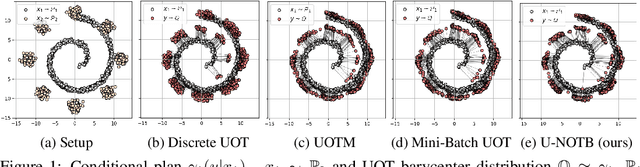
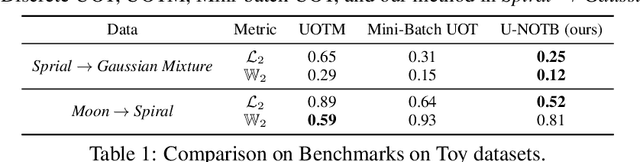
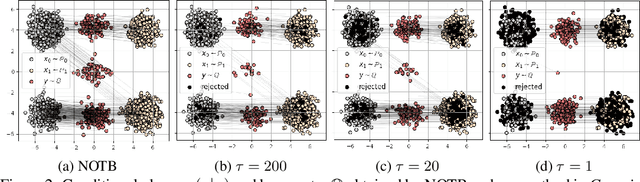
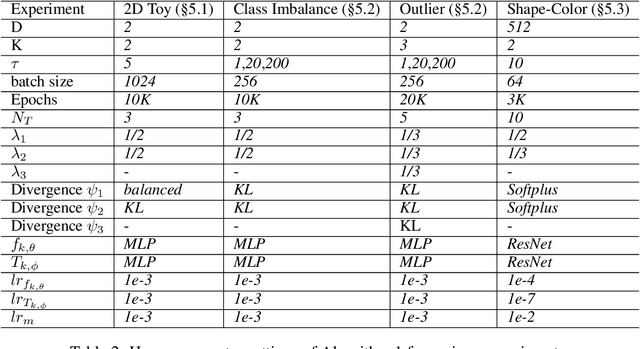
A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge